Q1. The angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level is called:
Solution
The angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level is called angle of elevation.
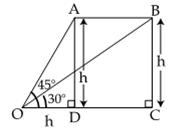
Q2. Two
men on either side of a cliff, 60 m high, observe the angles of elevation of
the top of the cliff to be 45o and 60o respectively.
Find the distance between two men.
Solution
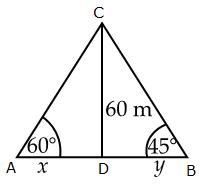 Let
A and B represent the position of the two men.
In
Let
A and B represent the position of the two men.
In

Q3. A tree
is broken by the wind. The top struck the ground at an angle of 30o
and at a distance of 30 metres from its root. Find the whole height of tree.
(Use 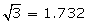 )
)
Solution
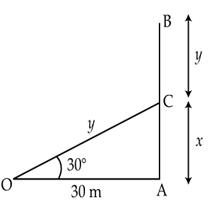 Let
AB be the tree. Suppose the tree is broken at C.
OC
= CB = y m
OA
= 30 m (given)
In
Let
AB be the tree. Suppose the tree is broken at C.
OC
= CB = y m
OA
= 30 m (given)
In
Q4. An aricraft is flying at constant height with a speed of 360 km/hours. From a point on the ground, the angle of elevation at an instant was observed to be 45o. After 20 seconds, the angle of elevation was observed to be 30o. Determine the height at which the aircraft is flying. (Use 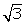 = 1.732
= 1.732
Solution
 Distance AB = Speed
Distance AB = Speed  In right
In right
Q5. Two buildings face each other. The height of one building is greater than that of the other. The smaller building is 80 m high. The angles of depression of the top and the bottom of the smaller building from the top of the taller building are 45º and 60º respectively. Find the height of the taller building.
Solution
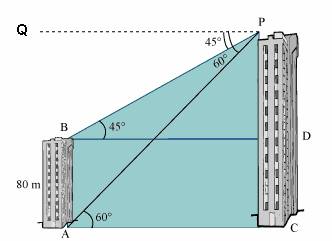 In the given figure, PC denotes the taller building and AB denotes the 80 m tall building.
We are interested in determining the height of the taller building, I which is., PC
If we look at the figure carefully and observe that PB is a transversal to the parallel lines PQ and BD.
Therefore,
In the given figure, PC denotes the taller building and AB denotes the 80 m tall building.
We are interested in determining the height of the taller building, I which is., PC
If we look at the figure carefully and observe that PB is a transversal to the parallel lines PQ and BD.
Therefore,  QPB and
QPB and  PBD are alternate angles, and are equal.
So,
PBD are alternate angles, and are equal.
So,  PBD = 45º. Similarly,
PBD = 45º. Similarly,  PAC = 60º.
In the right angled triangle PBD, we have
PAC = 60º.
In the right angled triangle PBD, we have

Q6. From an aero- plane vertically above a straight horizontal road, the angles of depression of two consecutive mile stones on opposite sides of the aero-plane are observed to be
 and
and
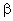 . Show that the height in miles of the aero-plane above the road is given by
. Show that the height in miles of the aero-plane above the road is given by
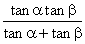
Solution
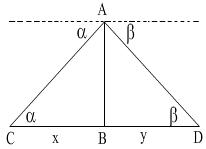 Let AB be the height of the aero-plane = h miles, C and D be the positions of two consecutive mile stones on opposite sides of the aero-plane.
Let the distance CB = x, and DB = y
From the figure,
Let AB be the height of the aero-plane = h miles, C and D be the positions of two consecutive mile stones on opposite sides of the aero-plane.
Let the distance CB = x, and DB = y
From the figure, 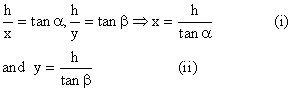 Adding ( i ) and (ii)
Adding ( i ) and (ii)
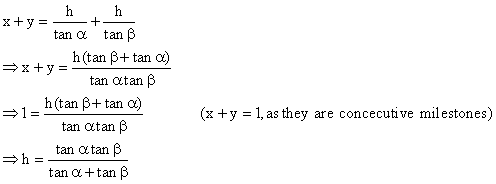
Q7. A tree casts a shadow 4 m long on the ground, when the angle of elevation of the sun is 45o. The height of the tree is:
Solution
 Let AB represent the tree and BC be its shadow.
Given, BC = 4 m
We have:
Let AB represent the tree and BC be its shadow.
Given, BC = 4 m
We have:
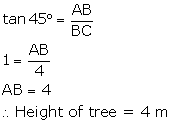
Q8. A
player sitting on the top of a tower
of height 20 m observes the angle of depression of a ball lying on the ground
as 60o. Find the distance between the foot of the tower and the
ball.
Solution
For
correct figure
 Let
C be the point where the ball is.
Let
C be the point where the ball is.
 C = 60o (alternate angles)
In
C = 60o (alternate angles)
In
 ABC, tan 60o = AB/BC
ABC, tan 60o = AB/BC
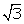 = 20/x
x = 20/
= 20/x
x = 20/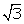 = 20 (
= 20 (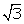 /3)
= 11.53 m
/3)
= 11.53 m
 Let
C be the point where the ball is.
Let
C be the point where the ball is.
Q9. The fig., shows the observation of point C from point A. The angle of depression from A is:
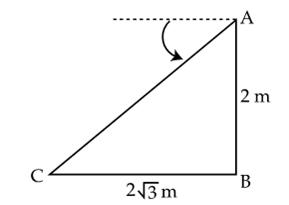

Solution
Let  be the angle of depression. Then,
be the angle of depression. Then, 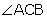 will also be
will also be  .
tan
.
tan  =
= 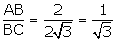 = tan 30o
Hence, the angle of depression,
= tan 30o
Hence, the angle of depression,  = 30o
= 30o
Q10. If the height and length of the shadow of a man are the same, then the angle of elevation of the sun is
Solution
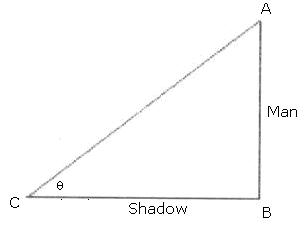 In the figure, AB is the height of the man and BC is his shadow.
Given that, AB = BC
In
In the figure, AB is the height of the man and BC is his shadow.
Given that, AB = BC
In 
Q11. A kite is flying at a height of 90 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60o. Find the length of the string assuming that there is no slack in the string [Take 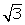 = 1.732]
= 1.732]
Solution

Q12. The angle of depression from the top of a tower 12 m high, at a point on the ground is 30o. The distance of the point from the top of the tower is:
Solution
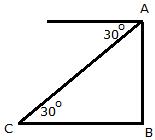 In the figure, AB denotes the tower of height 12 m.
In
In the figure, AB denotes the tower of height 12 m.
In 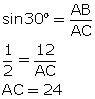 Thus, the required distance of the point from the top of the tower is 24 m.
Thus, the required distance of the point from the top of the tower is 24 m.
Q13. If sun's elevation is 60o then a pole of height 6 m will cast a shadow of length
Solution
 In the figure, AB denotes the pole of height 6 m and OA is its shadow.
In
In the figure, AB denotes the pole of height 6 m and OA is its shadow.
In 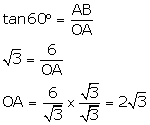 Thus, the length of the shadow of the pole is
Thus, the length of the shadow of the pole is
Q14. A
tower stands vertically on the ground. From a point on the ground which is 60
m away from the foot of the tower, the angle of elevation of the top of the
tower is found to be 60o. Find the height of the tower.
Solution
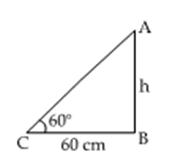 Let
h be the height of the tower.
In
Let
h be the height of the tower.
In
Q15. The ratio of the length of rod and its shadow is 1: 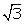 , then the angle of elevation of the sun is:
, then the angle of elevation of the sun is:
Solution
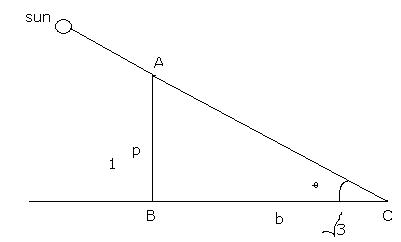 Here AB is the rod whose shadow is BC.
Here AB is the rod whose shadow is BC.
Q16. 

Solution
Q17. If the length of the shadow of a pole of height  is 3 m. find the angle of elevation of the sun.
is 3 m. find the angle of elevation of the sun.
 is 3 m. find the angle of elevation of the sun.
is 3 m. find the angle of elevation of the sun.Solution
Let AB be the pole and AC be its shadow.
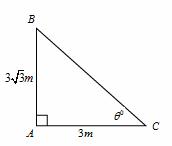 Let the angle of elevation,
Let the angle of elevation,  ACB = θ0
Then AB =
ACB = θ0
Then AB =  and AC = 3 m
and AC = 3 m

 Let the angle of elevation,
Let the angle of elevation,  ACB = θ0
Then AB =
ACB = θ0
Then AB =  and AC = 3 m
and AC = 3 m

Q18. John stands on the bridge and observes that the angles of depression of the banks on opposite sides of river Absyssa are 45º and 60º respectively. The bridge is at a height of 6 m from the banks. Calculate the width of the river Absyssa?
Solution
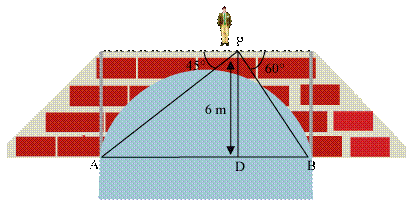 In the figure, let A and B represent points on the bank on opposite sides of the river Absyssa, so that AB is its width.
P is a point on the bridge at a height of 6 m, that is, DP = 6 m.
We have to calculate the width of the river, which is the length of the side AB of triangle APB.
Now, AB = AD + DB
In the right angled triangle APD, ÐA = 45º
In the figure, let A and B represent points on the bank on opposite sides of the river Absyssa, so that AB is its width.
P is a point on the bridge at a height of 6 m, that is, DP = 6 m.
We have to calculate the width of the river, which is the length of the side AB of triangle APB.
Now, AB = AD + DB
In the right angled triangle APD, ÐA = 45º
 Therefore, we have calculated the width of the river Absyssa to be equal to
Therefore, we have calculated the width of the river Absyssa to be equal to  m.
m.
Q19. From a
point on the ground the angle of elevation of the bottom and the top of a
flagstaff situated on the top of a 120 m tall house, was found to be 30o
and 45o respectively. Find the height of the flagstaff.
Solution
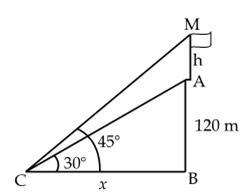 Let
AB (= 120 m) be the height of house and MA (= h) be the height of flagstaff.
In
Let
AB (= 120 m) be the height of house and MA (= h) be the height of flagstaff.
In
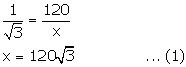 In
In
 Thus,
the height of the flagstaff is
Thus,
the height of the flagstaff is
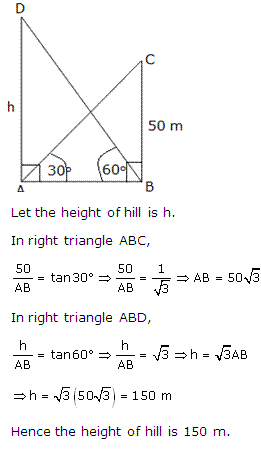
Q20. From
the top of hill the angles of depression of two consecutive kilometer stones
due east are found to be 30o and 60o. Find the height
of the hill.
Solution
For
the correct fig.
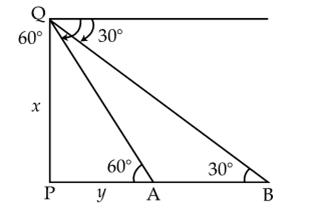 Let
PQ be the hill and A and B are the two kilometer stones.
Let
PQ be the hill and A and B are the two kilometer stones.
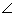 PAQ
= 60o, and
PAQ
= 60o, and 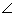 PBQ = 30o
In
PBQ = 30o
In
 PAQ, tan 60o = PQ/PA
PAQ, tan 60o = PQ/PA
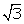 = x/y
y
= x/y
y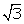 = x(i)
In
PBQ
tan
30o = PQ/PB
1/
= x(i)
In
PBQ
tan
30o = PQ/PB
1/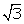 = x/(y + 1)
x
= (y + 1)/
= x/(y + 1)
x
= (y + 1)/ 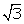 (ii)
3y
= y + 1
2y
= 1
y
= ½ km = 500 m
x
= 500
(ii)
3y
= y + 1
2y
= 1
y
= ½ km = 500 m
x
= 500 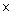 1.73 = 865 m
Height
of the hill = 865 m
1.73 = 865 m
Height
of the hill = 865 m
 Let
PQ be the hill and A and B are the two kilometer stones.
Let
PQ be the hill and A and B are the two kilometer stones.
Q21. From a
window, 60 m high above the ground, of a house in a street, the angles of elevation
and depression of the top and foot of another house on the opposite side of
the street are 60o and 45o respectively. Show that the
height of the opposite house is 60 (1 +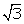 ) metres.
) metres.
Solution
 Let
E be the window which is 60 m above the ground, AC be the other house.
In
Let
E be the window which is 60 m above the ground, AC be the other house.
In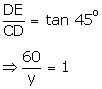
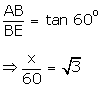
Q22. The
angle of elevation of the top of a tower at a point on the ground is 45o.
After going 40 m towards the foot of the tower, the angle of elevation of the
top of tower changes to 60o. Find the height of the tower. (use 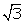 = 1.73)
= 1.73)
Solution
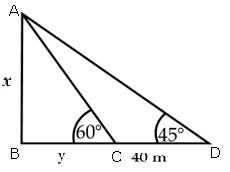 Let AB be the tower. Let C and D be the points on the
ground.
In
Let AB be the tower. Let C and D be the points on the
ground.
In 
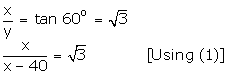

Q23. From
the top of a light house the angle of depression of a ship sailing towards it
was found to 30o. After 10 seconds the angle of depression changes
to 60o. Assuming that the ship is sailing uniform speed, from how
much it will take to reach the light house?
Solution
 Let
AC be the light house of height h.
The
two positions of the ship are D and B. DB is the distance covered by ship in
10 seconds.
In
Let
AC be the light house of height h.
The
two positions of the ship are D and B. DB is the distance covered by ship in
10 seconds.
In

Q24. An
electric pole is 10 m high. If its shadow is 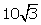 m in length.
Find the angle of elevation of the sun at that time.
m in length.
Find the angle of elevation of the sun at that time.
Solution
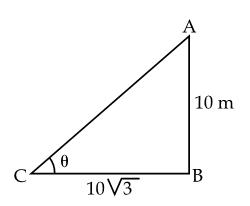 In
the figure, AB is the tower and BC denotes its shadow.
Let
In
the figure, AB is the tower and BC denotes its shadow.
Let
Q25. Find
the height of a mountain if the elevation of its top at an unknown distance
from the base is 60o and at a distance 10 km further off from the
mountain, along the same line, the angle of elevation is 30o.
Solution
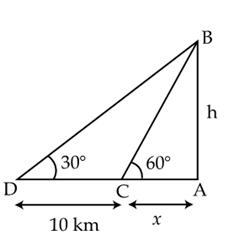 Let
h be the height of the mountain.
In
Let
h be the height of the mountain.
In
Q26. A man on the top of a vertical tower
observes a car moving towards the tower. If it takes 12 minutes for the angle
of depression to change from 30o to 45o, how soon after
this car will reach the tower? (see figure)
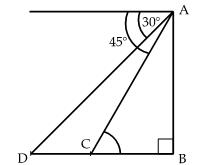

Solution
Let
the speed of the car be x units/min. Then, DC = 12x
 Let
the height of the tower be h units.
We
have:
Let
the height of the tower be h units.
We
have:  ACB = 45o and
ACB = 45o and 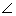 ADB = 30o
In
right triangle ABC,
tan
45o =
ADB = 30o
In
right triangle ABC,
tan
45o = 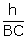 h
= BC
In
right triangle ABD,
tan
30o =
h
= BC
In
right triangle ABD,
tan
30o = 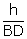
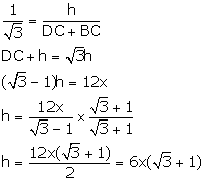
 Required
time taken by the car to reach the tower
=
Required
time taken by the car to reach the tower
=
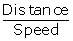 =
=
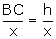 =
=
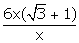 =
6(1.732 + 1)
=
16.392 minutes
=
6(1.732 + 1)
=
16.392 minutes
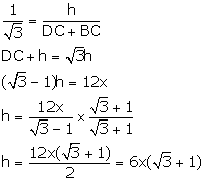
Q27. A
circus artist is climbing a rope 12 m long which is tightly stretched and
tied from the top of a vertical pole to the ground. Find the height of the
pole if the angle made by the rope with the ground is 30o.
Solution
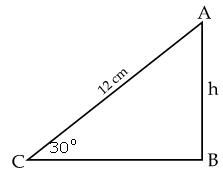 In
the figure, AB represents the pole and C is the point on the ground.
Let
the height of the pole be h.
In
In
the figure, AB represents the pole and C is the point on the ground.
Let
the height of the pole be h.
In
Q28. An
aeroplane at an altitude of 200 m observes the angles of depression of two
opposite points on two banks of the river to be 45o and 60o.
Find in metres, the width of the river. (use  = 1.732)
= 1.732)
Solution
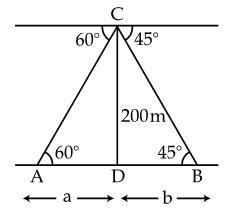 In
the figure, C denotes the position of the aeroplane. Points A and B denotes
the position of the two points on two banks of the river.
We
have to find AB, i.e., a + b
In
In
the figure, C denotes the position of the aeroplane. Points A and B denotes
the position of the two points on two banks of the river.
We
have to find AB, i.e., a + b
In
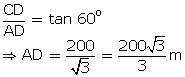 In
In
Q29. A boy
2 m tall is standing at some distance from a 30 m tall building. The angle of
elevation from his eyes of the top of the building increases form 30o
to 60o as he walks towards the building. Find the distance he
walked towards the building.
Solution
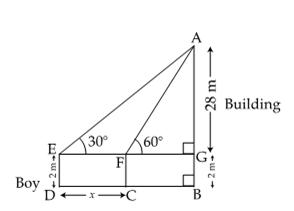 In
In
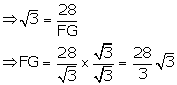 In
In

Q30. 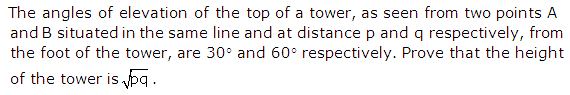
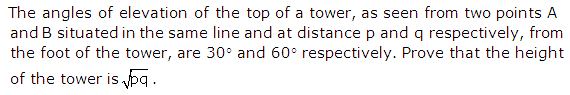
Solution

Q31. Distance between two buildings is 130 m. The angle of elevation of the top of the first building when seen from the second building is 45o. If the height of the second building is 70 m, find the height of the first building.
Solution
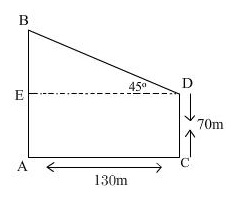 Let AB and CD be the two buildings of height h m and 60 m respectively.
AC = 130 m. The angle of elevation of top of AB as seen from top of CD is 45o
In triangle DEB,
Let AB and CD be the two buildings of height h m and 60 m respectively.
AC = 130 m. The angle of elevation of top of AB as seen from top of CD is 45o
In triangle DEB,
Q32. A ladder is leaning against a wall making an angle of 600 with the ground. Find the distance of the foot of the ladder from the wall if the other end is 14 m above the ground?
Solution
Let AB be the wall and BC be the ladder.
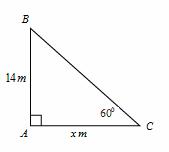 angle of elevation, ∠ACB = 600
Then AB = 14 m and let AC = x m
angle of elevation, ∠ACB = 600
Then AB = 14 m and let AC = x m
 Distance of the foot of the ladder from the wall is 7 m.
Distance of the foot of the ladder from the wall is 7 m.
 angle of elevation, ∠ACB = 600
Then AB = 14 m and let AC = x m
angle of elevation, ∠ACB = 600
Then AB = 14 m and let AC = x m
 Distance of the foot of the ladder from the wall is 7 m.
Distance of the foot of the ladder from the wall is 7 m.
Q33. 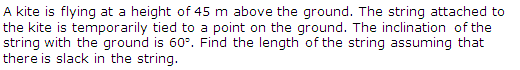
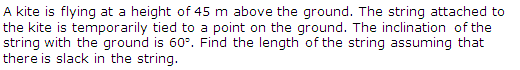
Solution
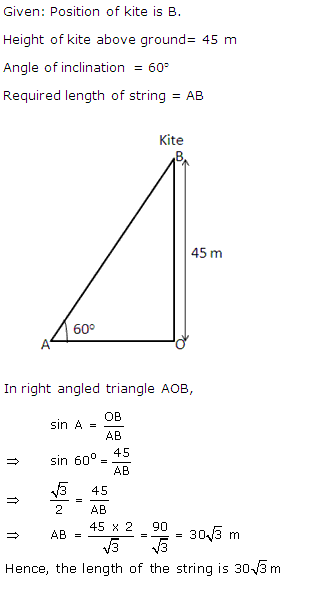
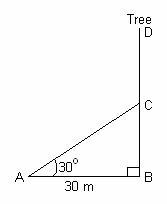
Q34. A tree is broken by the wind. The top struck the ground at an angle of 30o and at a distance of 30 metres from the root. Find the whole height of the tree.
Solution
Let BD be the whole height of the tree
The tree breaks at point C and makes 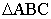 as given into the figure such that
AC = CD
as given into the figure such that
AC = CD
 In rt.
In rt. 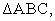
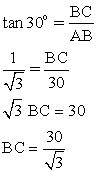 Also
Also

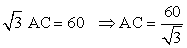
 Total height of tree = BC + AC
Total height of tree = BC + AC
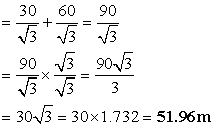
 In rt.
In rt. 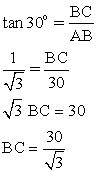 Also
Also
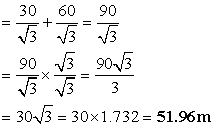
Comments
Post a Comment