Q1. How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid of dimensions 11 cm  10 cm
10 cm  7 cm? (take
7 cm? (take  )
)
 )
)Solution
Diameter of the coin = 1.75 cm  Radius, r =
Radius, r = 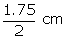 Height = 2 mm = 0.2 cm
Volume of 1 coin =
Height = 2 mm = 0.2 cm
Volume of 1 coin = 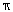 r2h =
r2h = 
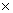 0.2 cm3
Volume of cuboid = 11
0.2 cm3
Volume of cuboid = 11 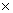 10
10 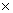 7 cm3
Since, the coins are melted to form a cuboid, so the total volumes of all coins will be equal to the volume of the cuboid.
Let the number of coins be n.
So, volume of n coins = volume of cuboid
7 cm3
Since, the coins are melted to form a cuboid, so the total volumes of all coins will be equal to the volume of the cuboid.
Let the number of coins be n.
So, volume of n coins = volume of cuboid
 n =
n = 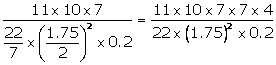 = 1600
= 1600
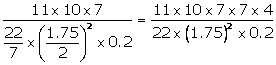 = 1600
= 1600
Q2. If the radius and slant height of a cone are equal, then the surface area of the cone will be
Solution
The surface area of a cone = 𝜋r(l + r)
According to the question,
l = r
The surface area of the cone = πr(l + l)
= πr(r + r) = 2πr2 or 2πl2
Q3. The interior of a building is in the form of a right circular cylinder of diameter 4.2 m and height 4m surmounted by a cone of vertical height 2.1 m. Find the volume of the building.
Solution
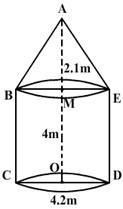

Q4. A cylinder and a cone are of the same base radius, but the height of the cone is four times that of the cylinder. The ratio of the volume of the cylinder to that of the cone is
Solution
Volume of a cylinder = πr2h
According to the question,
For a cone: H = 4h, where H and h are the heights of the cone and cylinder, respectively.
Volume of the cone =  The ratio of the volume is
The ratio of the volume is
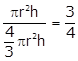
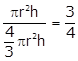
Q5. If a solid right circular cone of height 24 cm and base radius 6 cm is melted and recast in the shape of a sphere, then the radius of the sphere is
Solution
Here the volume of the cone will be equal to the volume of the sphere as the sphere is formed by the melting the cone.
Let the radius of sphere = R
Radius of cone = r, Height of cone = h
Thus, we have
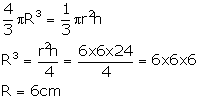
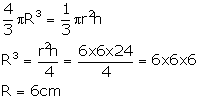
Q6. The internal radii of the ends of a bucket, full of milk and of internal height 16 cm are 14 cm and 7 cm. If this milk is poured into a hemispherical vessel, find the internal diameter of the vessel.
Solution
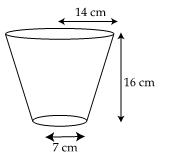 For bucket, h = 16 cm
r1 = 14 cm
r2 = 7 cm
V1 = Volume of bucket =
For bucket, h = 16 cm
r1 = 14 cm
r2 = 7 cm
V1 = Volume of bucket =  Let R cm be the radius of the hemispherical vessel
V2 = volume of vessel =
Let R cm be the radius of the hemispherical vessel
V2 = volume of vessel = 
Q7. A container is in the form of the frustum of a cone. If its height is 16 cm and the radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the slant height of the container and also the cost of milk that the container can hold, if the cost of milk is Rs. 30/litre (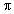 = 3.14)
= 3.14)
Solution
R = 20 cm, r = 8 cm, h = 16 cm
Slant height = 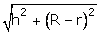 =
=  Volume =
Volume = 



Q8. A vessel is in the form of a hollow
hemisphere mounted by a hollow cylinder of same radius. The diameter of the
hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the
inner surface area of the vessel.
Solution
 Radius
of hemisphere = Radius of cylinder = 7 cm
Height
of cylinder = 13 cm - 7 cm = 6 cm
Inner
S.A. of vessel = Curved S.A. of cylindrical part + Curved S.A of
hemispherical part
Radius
of hemisphere = Radius of cylinder = 7 cm
Height
of cylinder = 13 cm - 7 cm = 6 cm
Inner
S.A. of vessel = Curved S.A. of cylindrical part + Curved S.A of
hemispherical part

Q9. The diameter of a sphere is 12 cm. It is melted and drawn into a wire of diameter 6 mm. The length of the wire is
Solution
For a sphere, d = 12 cm, r = 6 cm
For a cylindrical wire, d = 0.6 cm, r = 0.3 cm
Let the length of the wire be x cm.
According to the question,
π(0.3)2h =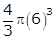
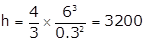 h = 3200 cm = 32 m
h = 3200 cm = 32 m
Q10. 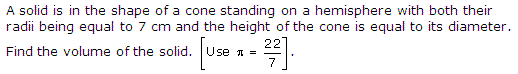
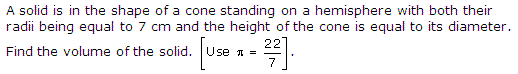
Solution

Q11. A cylinder whose height is 4/3 of its radius has the same volume as a sphere of radius 8 cm. The radius of the base of the cylinder will be
Solution
For a cylinder: h = 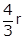 Volume of the cylinder = πr2h =
Volume of the cylinder = πr2h = 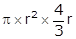 =
=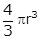 For a sphere: d = 8 cm, r = 4 cm
Volume of the sphere =
For a sphere: d = 8 cm, r = 4 cm
Volume of the sphere = 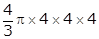 According to the question,
According to the question,
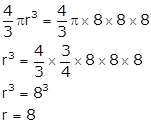 The radius of a sphere is 8 cm.
The radius of a sphere is 8 cm.
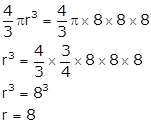 The radius of a sphere is 8 cm.
The radius of a sphere is 8 cm.
Q12. A solid is hemispherical at the bottom and conical above. If the curved surface area of the two parts are equal, then find the ratio of the radius and height of the conical part.
Solution
S.A. of hemisphere = S.A. of cone
2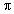 r2 =
r2 = 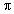 rl
2r = l
So, h =
rl
2r = l
So, h = 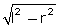 h =
h = 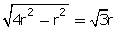 h = r
h = r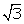 r : h = r : r
r : h = r : r 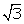 = 1 :
= 1 : 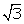
Q13. A right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution
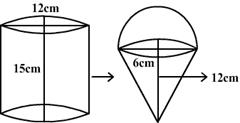

Q14. The given figure represents a solid consisting of a cylinder surmounted by a cone at one end and a hemisphere at the other end. Find the curved surface area of the solid. 

Solution

Q15. If the radius of base of a cylinder is doubled and the height remains unchanged, its curved surface area becomes
Solution
Original radius = r (say)
New radius = 2r
Height = h
Original curved surface area = 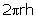 New curved surface area =
New curved surface area = 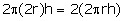 Thus, the curved surface area also becomes double.
Thus, the curved surface area also becomes double.
Q16. How
many solid spheres of diameter 6 cm are required to be melted to form a solid
metal cylinder of height 45 cm and diameter 4 cm?
Solution
Let
n be the required number of spheres.
Since,
the spheres are melted to form a cylinder. So, the volume of all the n
spheres will be equal to the volume of the cylinder.

 n = 5
Thus,
the required number of spheres which are melted to form the cylinder is 5.
n = 5
Thus,
the required number of spheres which are melted to form the cylinder is 5.
Q17. A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted and cast into a cone of base diameter 8 cm. Find the height of the cone.
Solution
External diameter of sphere = 8 cm  radius, R = 4 cm
Internal diameter of sphere = 4 cm
radius, R = 4 cm
Internal diameter of sphere = 4 cm  radius, r = 2 cm
Diameter of the base of cone = 8 cm
radius, r = 2 cm
Diameter of the base of cone = 8 cm  radius = 4 cm
Now, Volume of the cone = Volume of the material in the sphere
radius = 4 cm
Now, Volume of the cone = Volume of the material in the sphere
 Hence, the height of the cone = 14 cm
Hence, the height of the cone = 14 cm
 radius, R = 4 cm
Internal diameter of sphere = 4 cm
radius, R = 4 cm
Internal diameter of sphere = 4 cm  radius, r = 2 cm
Diameter of the base of cone = 8 cm
radius, r = 2 cm
Diameter of the base of cone = 8 cm  radius = 4 cm
Now, Volume of the cone = Volume of the material in the sphere
radius = 4 cm
Now, Volume of the cone = Volume of the material in the sphere
 Hence, the height of the cone = 14 cm
Hence, the height of the cone = 14 cm
Q18. The
diameter of a metallic solid sphere is 9 cm. It is melted and drawn into a
wire having diameter of cross-section as 0.2 cm. Find the length of the wire.
Solution
For
sphere:
d
= 9 cm 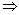 r =
r = 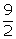 cm
Volume
of sphere =
cm
Volume
of sphere = 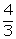
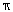 r3 =
r3 = 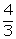
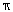
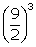 cu. cm
For
wire/ cylinder:
Diameter
of cylinder = 0.2 cm
cu. cm
For
wire/ cylinder:
Diameter
of cylinder = 0.2 cm  R = 0.1 cm
Volume
of cylinder =
R = 0.1 cm
Volume
of cylinder = 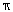 r2h =
r2h = 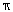 (0.1)2 h
The
sphere is melted to form a cylindrical wire.
(0.1)2 h
The
sphere is melted to form a cylindrical wire.
 Volume
of sphere = volume of cylinder
Volume
of sphere = volume of cylinder
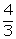
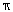
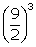 =
= 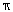 (0.1)2h
h
=
(0.1)2h
h
=  = 12150 cm =
121.5 m
Thus,
the length of the wire is 121.5 m.
= 12150 cm =
121.5 m
Thus,
the length of the wire is 121.5 m.
Q19. Radii of the cylinder and sphere are the same, and the height of the cylinder is twice its radius. Find the ratio of the volume of the cylinder to the sphere.
Solution
For a cylinder: h = 2r
Volume of the cylinder = πr2h = πr2(2r) = 2πr3 For a sphere:
Volume of the sphere = 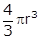 The required ratio is
The required ratio is
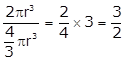
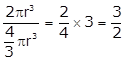
Q20. Three cubes of volume 64 cm3 each are joined end to end to form a solid. Find the surface area of the cuboid so formed.
Solution
Volume of each cube = 64 cm3
Thus, side of each cube = 4 cm
So, the dimensions of cuboid are 4 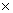 4
4 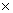 12.
12.
 Surface area of the cuboid = 2[4
Surface area of the cuboid = 2[4 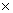 4 + 4
4 + 4 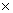 12 + 12
12 + 12 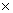 4]
= 224 sq. cm
4]
= 224 sq. cm
Q21. The slant height of the frustum of a cone
is 5 cm. If the difference between the radii of its two circular ends is 4
cm, find the height of the frustum.
Solution
Let
r and R be radii of the circular ends of the frustum of the cone.
Then,
R - r = 4, l = 5
We
know l2 = (R - r)2
+ h2
52
= 42 + h2
h2
= 25 - 16 = 9
h
= 3
Thus,
the height of the frustum is 3
cm.
Q22. If the radius of the base of a right circular cylinder is halved, keeping the height same, find the ratio of the volume of the reduced cylinder to that of the original cylinder.
Solution

Q23. 

Solution
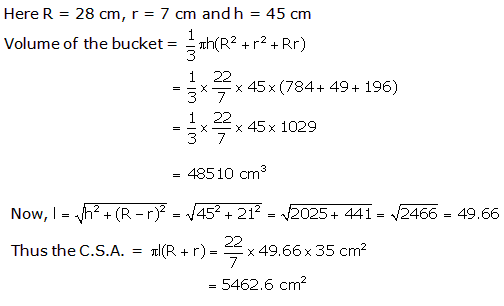
Q24. The curved surface area of a right circular cone of height 15 cm and base diameter 16 cm is
Solution
Height = 15 cm
Diameter = 16 cm
So, radius = 8 cm
Slant height = l = 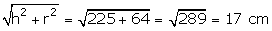 Curved surface area =
Curved surface area = 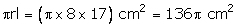
Q25. A milk container is made of a metal sheet in the form of a frustum of a cone of height 16 cm, with radii of lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which the container can hold when full at Rs. 20 per litre.
Solution
Height, h = 16 cm
Radius of upper end = R = 20 cm
Radius of lower end = r = 8 cm
Volume of container = 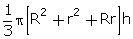
 = 10449.92 cm3
= 10.45 litres
Cost of milk = Rs. (20
= 10449.92 cm3
= 10.45 litres
Cost of milk = Rs. (20  10.45) = Rs. 209
10.45) = Rs. 209
 = 10449.92 cm3
= 10.45 litres
Cost of milk = Rs. (20
= 10449.92 cm3
= 10.45 litres
Cost of milk = Rs. (20
Q26. A solid sphere of diameter 14 cm is cut
into two halves by a plane passing through the centre. Find the combined
surface area of the two hemispheres so formed.
Solution
Radius
of each hemisphere = 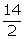 cm = 7 cm
Surface
area of one hemisphere = 3
cm = 7 cm
Surface
area of one hemisphere = 3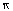 r2
Surface
area of two hemispheres (same radius)
=
6
r2
Surface
area of two hemispheres (same radius)
=
6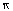 r2
=
r2
=
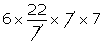 =
924 cm2
=
924 cm2
Q27. A
vessel in the form of a hemispherical bowl is full of water. Its water is emptied
in to a cylinder. The internal radii of bowl and the cylinder are 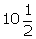 cm and 7 cm
respectively. Find the height of water in the cylinder.
cm and 7 cm
respectively. Find the height of water in the cylinder.
Solution
Radius
of hemispherical vessel = 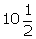 cm =
cm =  cm
Volume
of water in hemispherical vessel =
cm
Volume
of water in hemispherical vessel = 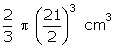 Let
h be the height of water in the cylinder.
Radius
of cylinder = 7 cm
Volume
of water in cylinder =
Let
h be the height of water in the cylinder.
Radius
of cylinder = 7 cm
Volume
of water in cylinder = 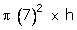 cm3
cm3
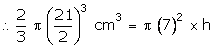 h
=
h
= 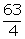 cm = 15.75 cm
cm = 15.75 cm
Q28. The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume is one- twenty seventh of the given cone, at what height above the base, the section is made.
Solution

Q29. A cylindrical copper rod of diameter 1 cm and length 8 cm is drawn into a cylindrical wire of length 18 m and uniform thickness. Find the thickness of the wire.
Solution
Volume of the rod =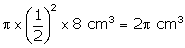 The cylindrical copper rod is drawn into a cylindrical wire. So, their volume is the same.
Length of the new wire = 18 m = 1800 cm
Let r be the radius of the cross-section of the wire.
Volume of the wire =
The cylindrical copper rod is drawn into a cylindrical wire. So, their volume is the same.
Length of the new wire = 18 m = 1800 cm
Let r be the radius of the cross-section of the wire.
Volume of the wire = 
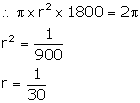 So, the diameter of the cross-section, i.e., the thickness of the wire is
So, the diameter of the cross-section, i.e., the thickness of the wire is 
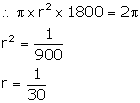 So, the diameter of the cross-section, i.e., the thickness of the wire is
So, the diameter of the cross-section, i.e., the thickness of the wire is 
Q30. If the surface area of a sphere is 144 cm2, then its radius is
cm2, then its radius is
 cm2, then its radius is
cm2, then its radius isSolution
Let r be the radius of the sphere.
Surface area of a sphere = 4 r2
144
r2
144 = 4
= 4 r2
r2 = 36
r = 6 cm
r2
r2 = 36
r = 6 cm
 r2
144
r2
144 = 4
= 4 r2
r2 = 36
r = 6 cm
r2
r2 = 36
r = 6 cm
Q31. A wooden article was made by scooping out a hemisphere from each end of a cylinder. If the height of the cylinder is 15 cm, and the base is of diameter 14 cm, find the total surface area of the article when it is ready.
Solution


Q32. A hemispherical bowl of internal radius 9 cm contains a liquid. This liquid is filled in small cylindrical bottles of diameter 3 cm and height 4 cm. Determine the number of bottles used to empty the bowl.
Solution

Q33. 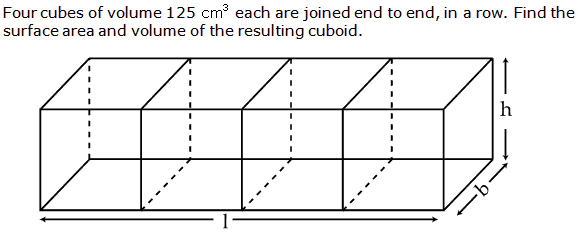

Solution

Q34. The surface area of a sphere is equal to the surface area of a cube whose radius is 21 cm. Find the side of the cube.
Solution
Surface area of a sphere = 4𝜋r2
Surface area of a cube = 6l2
According to the question,
4𝜋r2= 6l2
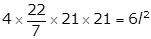
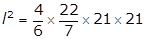 l = 30.39 cm
l = 30.39 cm
Q35. If the radii of circular ends of frustum of a cone are 20 cm and 12 cm and its height is 6 cm, then the slant height of frustum (in cm) is:
Solution

Q36. The volume of a largest sphere than can be cut from cylindrical log of wood of base radius 1 m and height 4 m is:
Solution
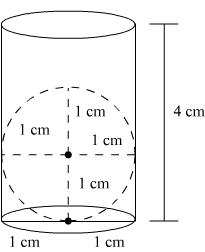 Let r be the radius of the largest sphere which can be cut off from the cylindrical log of wood whose radius is 1 cm and height is 4 cm.
From the given figure, we have:
r = 1 cm
Let r be the radius of the largest sphere which can be cut off from the cylindrical log of wood whose radius is 1 cm and height is 4 cm.
From the given figure, we have:
r = 1 cm
Q37. The volume of a cube is half of its surface area. The side of the cube (in cm) is
Solution
The surface area of a cube is 6s2.
The volume of the cube is s3.
According to the question,
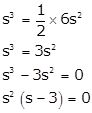 s ≠ 0
Hence, s = 3 cm.
s ≠ 0
Hence, s = 3 cm.
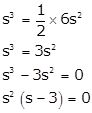 s ≠ 0
Hence, s = 3 cm.
s ≠ 0
Hence, s = 3 cm.
Q38. A bucket is made up of a metal sheet in the form of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of the bucket if the cost of the metal sheet is Rs. 15 per 100 cm2.
Solution
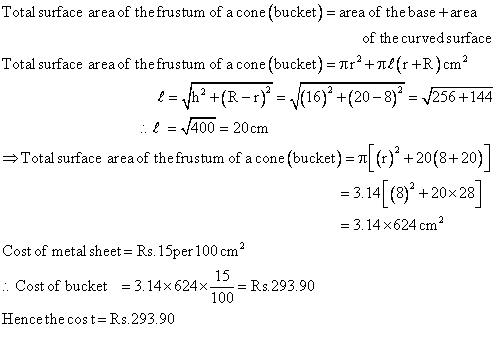
Q39. How
many lead shots, each 0.3 cm in diameter, can be made from a cuboid
dimensions 9 cm  11 cm
11 cm  12 cm
12 cm 
Solution
Volume
of cuboid = Total volume of lead shots=no. of lead shots 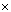 Volume of one
lead shot
radius
of lead shots=
Volume of one
lead shot
radius
of lead shots=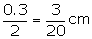 Let
n be the number of lead shots.
Let
n be the number of lead shots.
 9
9 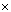 11
11 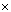 12 = n
12 = n 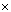
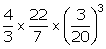 n
=
n
=  = 84000
= 84000
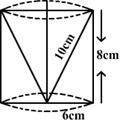
Q40. From a solid cylinder, whose height is 8 cm and radius 6 cm, a conical cavity of height 8 cm and of base radius 6 cm is hollowed out. Find the total surface area of the remaining solid.
Solution

Q41. 

Solution

Q42. A shuttle cock used for playing badminton has the shape of the combination of :
Solution
A shuttle cock used for playing badminton has the shape of the combination of a hemisphere and frustum cone.
Q43. The volume of a sphere (in cu. cm) is equal to its surface area (in sq. cm). The diameter of the sphere (in cm) is
Solution
Volume of the sphere = Surface area of the sphere
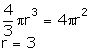 Thus, the diameter of the sphere is 6 cm.
Thus, the diameter of the sphere is 6 cm.
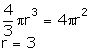 Thus, the diameter of the sphere is 6 cm.
Thus, the diameter of the sphere is 6 cm.
Q44. The rain water from a roof 20 m by 20 m drains out into a cylindrical vessel having diameter of base 2 m and height 3.5 m. If the vessel is just full, find the rainfall in cm.
Solution
 Hence, the rainfall = 2.75 cm
Hence, the rainfall = 2.75 cm
Q45. A semi-circular sheet of paper of diameter
28 cm is bent into an open conical cup. Find the depth and capacity of the
cup.
Solution
When the semi-circular sheet is bent into an open conical cup, the
radius of the sheet becomes the slant height of the cup and the circumference
of the sheet becomes the circumference of the base of the cone.
l = Slant height of the conical cup = 14 cm
Let r be the radius of and h be the height of the conical cup.
Circumference of the base of the conical cup = circumference of the
sheet
2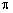 r =
r = 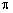
 14
14
 r = 7 cm
h
=
r = 7 cm
h
= 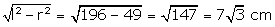 = 12.12 cm
Capacity
of the cup = Volume of the cup
=
= 12.12 cm
Capacity
of the cup = Volume of the cup
=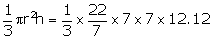 = 622.16 cm3
= 622.16 cm3
Q46. 

Solution

Q47. If a cone is cut into two parts by a horizontal plane passing through the mid-points of its axis, the ratio of the volumes of the upper part and the cone is
Solution
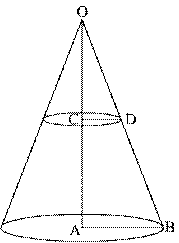 Let the height and radius of the given cone be H and R respectively.
Let the height and radius of the given cone be H and R respectively.
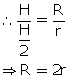 Volume of smaller cone =
Volume of smaller cone = 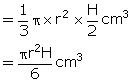 Volume of given cone
Volume of given cone

Q48. A rectangular sheet of paper 44 cm  18 cm
is rolled a along its length (44 cm) and a cylinder is formed. Find the
volume of the cylinder.
18 cm
is rolled a along its length (44 cm) and a cylinder is formed. Find the
volume of the cylinder.
Solution
Given,
a rectangular sheet of paper
44 cm  18 cm is
rolled a along its length to form a cylinder.
18 cm is
rolled a along its length to form a cylinder.
 Height
of cylinder = 18 cm
Circumference
= 44 cm
Height
of cylinder = 18 cm
Circumference
= 44 cm
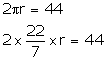 r
= 7 cm
Volume
of the cylinder =
r
= 7 cm
Volume
of the cylinder = 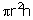
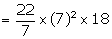 = 2772 cm3
= 2772 cm3
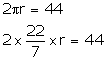 r
= 7 cm
Volume
of the cylinder =
r
= 7 cm
Volume
of the cylinder =
Q49. A tent is of the shape of a right circular cylinder upto a height of 3 metres and conical above it. The total height of the tent is 13.5 metres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs. 2 per square metre, if the radius of the base is 14 metres.
Solution
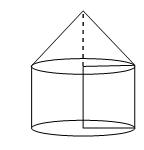 CSA of Tent = CSA of cylinder + CSA of cone
= 2
CSA of Tent = CSA of cylinder + CSA of cone
= 2
Q50. The diameter of a sphere is 9 cm. It is melted and drawn into a wire of diameter 9 mm. The length of the wire is
Solution
For a sphere, d = 9 cm, r = 4.5 cm
For a cylindrical wire, d = 0.9 cm, r = 0.45 cmLet the length of the wire be x cm.
According to the question,
Π(0.45)2h =  h = 600 cm = 6 m
h = 600 cm = 6 m
Q51. A cylinder and a cone are of the same base radius, but the height of the cone is double that of the cylinder. The ratio of the volume of the cylinder to that of the cone is
Solution
Volume of the cylinder = πr2h
According to the question,
For a cone: H = 2h, where H and h are the heights of the cone and cylinder, respectively.
Volume of the cone = 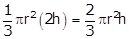 The ratio of the volume is
The ratio of the volume is 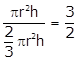
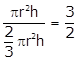
Q52. A
solid sphere of radius 3 cm is melted and drawn into a long wire of uniform
circular cross-section. If the length of the wire is 36 m, find its radius.
Solution
Wire
is cylindrical in shape.
Height
of the wire = 36 m = 3600 cm
Let
r be the radius of the wire.
Since,
the sphere is melted to form a wire, so the volume of the sphere will be
equal to the volume of the wire.
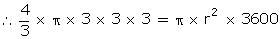
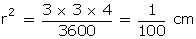 r
=
r
= 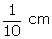 = 0.1 cm = 1
mm
Thus,
the radius of the wire is 1 mm.
= 0.1 cm = 1
mm
Thus,
the radius of the wire is 1 mm.
Q53. The radii of two cylinders are in the ratio 2:3. If their heights are in the ratio 3:5, then the ratio of their curved surface areas is
Solution
Curved surface area of a cylinder = 2πrh
Let r1 and r2 be the radii of the cylinders and h1
and h2 be the heights of the cylinders.
Ratio of curved surface areas =

Q54. Water in a canal 6 m wide and 1.5 m deep is flowing with a speed of 10 km/h How much area will it irrigate in 30 minutes if 8 cm of standing water is needed?
Solution
Consider an area of cross section of canal be ABCD.
Area of cross section = 6 × 1.5 = 9 m2
Speed of water = 10 km/h =  Volume of water that flows in 1 minute from canal =
Volume of water that flows in 1 minute from canal =  = 1500 m3
Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let irrigated area be A. Volume of water irrigated in the required area will be equal to the volume of water flowed in 30 minutes from canal.
Volume of water that flows in 30 minutes from canal = Volume of water irrigated in the required area
= 1500 m3
Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let irrigated area be A. Volume of water irrigated in the required area will be equal to the volume of water flowed in 30 minutes from canal.
Volume of water that flows in 30 minutes from canal = Volume of water irrigated in the required area
 So, area irrigated in 30 minutes is 562500 m2.
So, area irrigated in 30 minutes is 562500 m2.
 Volume of water that flows in 1 minute from canal =
Volume of water that flows in 1 minute from canal =  = 1500 m3
Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let irrigated area be A. Volume of water irrigated in the required area will be equal to the volume of water flowed in 30 minutes from canal.
Volume of water that flows in 30 minutes from canal = Volume of water irrigated in the required area
= 1500 m3
Volume of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let irrigated area be A. Volume of water irrigated in the required area will be equal to the volume of water flowed in 30 minutes from canal.
Volume of water that flows in 30 minutes from canal = Volume of water irrigated in the required area
 So, area irrigated in 30 minutes is 562500 m2.
So, area irrigated in 30 minutes is 562500 m2.
Q55. A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that the mass of 1 cm3 of iron is 8 gm.
Solution
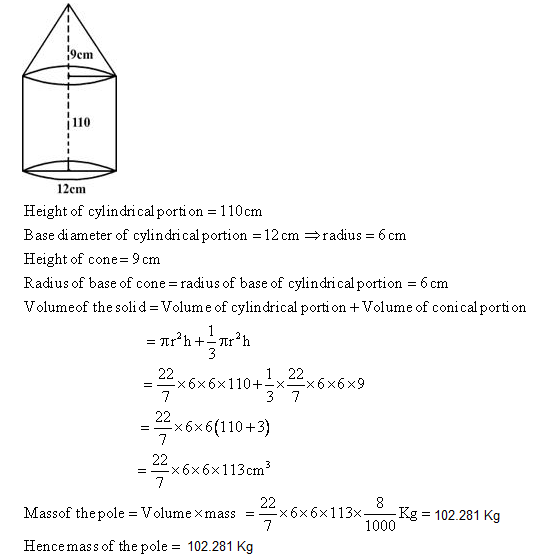
Q56. A
hemispherical bowl of internal diameter 36 cm is full of liquid. This liquid
is to be filled in cylindrical bottles of radius 3 cm and height 6 cm. How
many such bottles are required to empty the bowl?
Solution
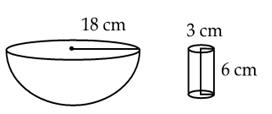 Volume
of liquid in hemispherical bowl
Volume
of liquid in hemispherical bowl 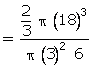 = 72
= 72
Q57. 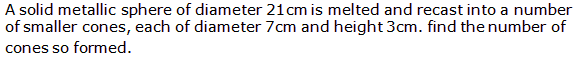
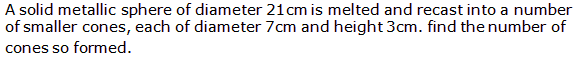
Solution
Q58. A well
of diameter 3 m is dug 14 m deep. The earth taken out of it is spread evenly
all around it to a width of 4 m, to form an embankment. Find the height of
the embankment. (Use 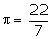 ).
).
Solution
Volume
of earth dug out =  = 99 m3
Let
h be height of embankment.
Now,
volume of embankment = Volume of earth
taken out
= 99 m3
Let
h be height of embankment.
Now,
volume of embankment = Volume of earth
taken out
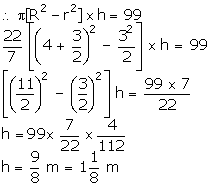
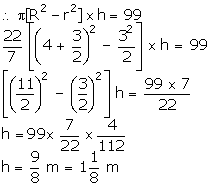
Q59. If the height of a right circular cylinder is doubled keeping the radius the same, then the ratio of the volume of the cylinder thus obtained to the volume of the original cylinder is
Solution
Volume of the cylinder = πr2h
The height is doubled keeping the radius the same. Volume of the new cone = πr2(2h) = 2πr2h
The ratio of the volume of the new cylinder to the original one is 2:1.
Q60. A container, open from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of Rs.20/ litre. Also find the cost of metal sheet used to make the container if it costs Rs. 8 per 100 cm2.
Solution

Q61. A girl fills a cylindrical bucket 32 cm in height and 18 cm in radius with sand. She empties the bucket on the ground and makes a conical heap of the sand. If the height of the conical heap is 24 cm, find the radius and the slant height of the heap. (Answer correct to one place of decimal)
Solution
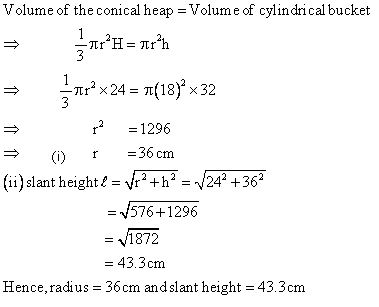
Q62. A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm3 of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making.
Solution

Q63. A
bucket made up of a metal sheet is in the form of a frustum of cone of height
16 cm with radii of its lower and upper ends 8 cm and 20 cm respectively.
Find the cost of the bucket if the cost of metal sheet used is Rs. 15 per 100
cm2. (use  = 3.14)
= 3.14)
Solution
 Here
r1 = 8 cm, r2 = 20 cm, h = 16 cm
l =
Here
r1 = 8 cm, r2 = 20 cm, h = 16 cm
l =
Q64. A solid iron pole consists of a cylinder of
height 220 cm and base diameter 24 cm, which is surmounted by cylinder of
height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3
of iron has 8 gm mass.
Solution
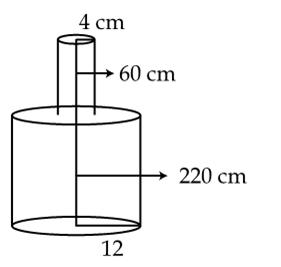 Vpole
= Vsmall cylinder + Vbig cylinder
Vpole
=
Vpole
= Vsmall cylinder + Vbig cylinder
Vpole
=
Q65. A circus tent consists of a cylindrical base surmounted by a conical roof. The radius of the cylinder is 20 m. The height of the tent is 63 m and that of the cylindrical base is 42 m. Find the area of the canvas used for making it.
Solution

Q66. Water
is flowing at the rate of 15 km per hour through a pipe of diameter 14 cm
into a rectangular tank which is 50 m long and 44 m wide. Find the time in
which the level of water in the tank will rise by 21 cm.
Solution
For
the tank, vol = l  b
b  h
= 50
h
= 50  44
44  0.21 m3
'r'
of pipe = 0.07 m
Vol
of pipe = vol of tank of height 21 cm
0.21 m3
'r'
of pipe = 0.07 m
Vol
of pipe = vol of tank of height 21 cm
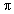 r2h1
= 50
r2h1
= 50 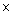 44
44 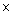 0.21
22/7
0.21
22/7
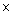 0.07
0.07  0.07
0.07  h1
= 50
h1
= 50  44
44  0.21
h1
= 30,000 = 30 km
Water
flows @ 15 km/hr, so time taken to cover 30 km = 30/15 = 2 hours
0.21
h1
= 30,000 = 30 km
Water
flows @ 15 km/hr, so time taken to cover 30 km = 30/15 = 2 hours
Q67. A circus tent made of canvas is in the form of right circular cylinder and a right circular cone above it. The diameter and height of the cylindrical part of the tent are 21 m and 4 m respectively. The slant height of conical part is 12.5 m. Find the area of the canvas used for making the tent. Also, find total cost of the tent if the canvas used is Rs. 12/sq metre.
Solution
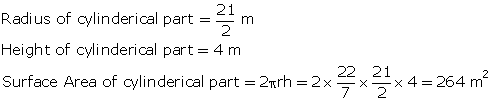 Slant height of conical part, l = 12.5 m
Radius of conical part =
Slant height of conical part, l = 12.5 m
Radius of conical part = 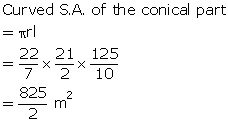 = 412.5 m2
Total Surface area = (264 + 412.5) m2 = 676.5 m2
Cost = Rs 12
= 412.5 m2
Total Surface area = (264 + 412.5) m2 = 676.5 m2
Cost = Rs 12
Q68. The
rain water from a roof 22 m  20 m drains
into a conical vessel having the diameter of base as 2 m and height 3.5 cm.
If the vessel is just full, find the rainfall in mm.
20 m drains
into a conical vessel having the diameter of base as 2 m and height 3.5 cm.
If the vessel is just full, find the rainfall in mm.
Solution
Let
the rainfall be h m.
Volume
of cuboid = (22  20
20 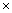 h) cu. m
Volume
of conical vessel =
h) cu. m
Volume
of conical vessel = 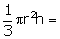
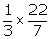
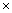 1
1 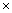 3.5 cu m
Volume
of cuboid = Volume of conical vessel
22
3.5 cu m
Volume
of cuboid = Volume of conical vessel
22
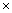 20
20 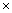 h =
h = 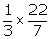
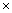 1
1 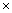 3.5
3.5


Q69. The rain water from a roof 22 m  20 m
drain in to a conical vessel having diameter of base as 2 m and height 3.5 m.
If the vessel if just full, find the rain fall in cm.
20 m
drain in to a conical vessel having diameter of base as 2 m and height 3.5 m.
If the vessel if just full, find the rain fall in cm.
Solution
Let
the rain fall be x cm.
Volume
of water collected on roof = 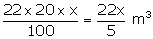 Volume
of water in conical vessel =
Volume
of water in conical vessel = 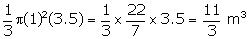
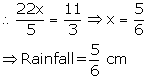
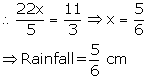
Q70. A solid is in the form of a right circular cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder and the hemispheres is 7 cm. Find the volume and total surface area of the solid.
Solution
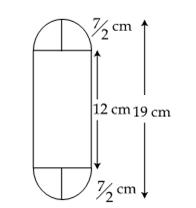 Let r be radius and h be the height of cylinder.
r =
Let r be radius and h be the height of cylinder.
r =
Q71. A toy is in the form of a cone of radius 3.5 cm surmounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy 
Solution
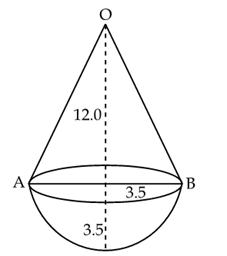 Radius of hemisphere = 3.5 cm
Total height of the toy = 15.5 cm
Height of the cone = 15.5 c m - 3.5 cm = 12.0 cm
Slant height (l) of the cone =
Radius of hemisphere = 3.5 cm
Total height of the toy = 15.5 cm
Height of the cone = 15.5 c m - 3.5 cm = 12.0 cm
Slant height (l) of the cone =
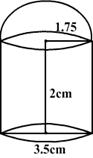
Q72. A cylindrical container 2 m high and 3.5 m in diameter has a hemispherical lid. Find its volume.
Solution

Q73. A spherical copper shell, of external
diameter 18 cm, is melted and recast into a solid cone of base radius 14 cm
and height  cm.
Find the inner diameter of the shell.
cm.
Find the inner diameter of the shell.
Solution
External
radius of copper shell, rc = 9 cm
Let
the internal radius of copper shell be ri.
Radius
of cone, rc = 14 cm
Height
= hc =  cm =
cm = 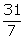 cm
Since,
the spherical copper shell is
melted and recast into a solid cone, their volumes are the same.
cm
Since,
the spherical copper shell is
melted and recast into a solid cone, their volumes are the same.

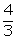
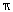 (rc3
- ri3) =
(rc3
- ri3) = 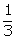
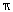 rc2
rc2 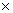 hc
hc


Q74. A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area of the toy.
Solution

Q75. Find
the volume of the largest right circular cone that can be out of a cube of
side 4.2 cm. 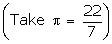
Solution
Diameter
of base of the cone = Side of the cube
 Radius of base of the cone =
Radius of base of the cone = 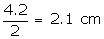
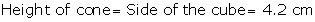
 Volume of cone cut out
Volume of cone cut out 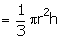
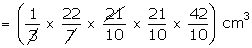 = 19.404
cm3
= 19.404
cm3
Q76. A gulab jamun, contains sugar syrup up to
about 30% of its volume. Find approximately how much syrup would be found in
45 such gulab jamuns, each shaped like a cylinder with two hemispherical ends
with total length 5 cm and diameter 2.8 cm.
Solution
It
is given that each gulab
jamuns is shaped like a cylinder with two hemispherical ends.
Radius of cylinder and hemispherical ends =
1.4 cm
Height of cylinder = 5 cm - 1.4 cm - 1.4 cm
= 2.2 cm
Volume
of 1 gulab jamun = 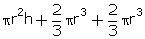 =
= 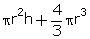 =
= 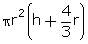 =
= 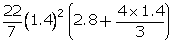 =
= 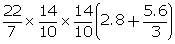 = 28.7
cm3
= 28.7
cm3
 Volume
of 45 gulab jamuns = 45
Volume
of 45 gulab jamuns = 45 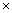 28.7 cm3
28.7 cm3
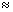 1292 cm3
1292 cm3
 Volume
of syrup in 45 gulab jamuns
Volume
of syrup in 45 gulab jamuns 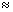
 cm3
cm3
 387.6 cm3
387.6 cm3
Q77. A solid is made of a cylinder with hemispherical ends. If the entire length of the solid is 108 cm and the diameter of the hemispherical ends is 36 cm, find the cost of polishing the surface of the solid at the rate of 7 paise per sq. cm.
Solution

Q78. The radius and slant height of a right circular cone are in the ratio of 7: 13 and its curved surface area is 286 cm2. Find its radius. (Use  =
=  )
)
 =
=  )
)Solution
For a given cone,
r = 7a , l = 13a
Thus, Curved Surface Area =  =
=  (7a)(13a) = 91
(7a)(13a) = 91 a2 = 286
or a2 =
a2 = 286
or a2 = 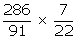 = 1
= 1
 a = 1
a = 1
 Radius of the cone = 7 cm.
Radius of the cone = 7 cm.
 =
=  (7a)(13a) = 91
(7a)(13a) = 91 a2 = 286
or a2 =
a2 = 286
or a2 =
Q79. Solid spheres of diameter 6 cm each are dropped into a cylindrical beaker containing some water and are fully submerged. The water in the beaker rises by 40 cm. Find the number of solid spheres dropped into the beaker if the diameter of the beaker is 18 cm.
Solution
Radius r of sphere =  = 3 cm
Volume of sphere =
= 3 cm
Volume of sphere = 
 r3
If R is the radius and H is the height of the cylinder, then
Volume of water in the cylindrical beaker =
r3
If R is the radius and H is the height of the cylinder, then
Volume of water in the cylindrical beaker =  R2H
Volume of rise in level of water =
R2H
Volume of rise in level of water = 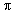 R2 (40)
R2 (40)
 If 'N' is the number of spheres dropped in the beaker then volume of spheres = Volume of water rose in the beaker
N
If 'N' is the number of spheres dropped in the beaker then volume of spheres = Volume of water rose in the beaker
N 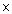

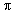 r3 =
r3 = 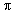 R2(40)
N
R2(40)
N 
 (3)3 = 9
(3)3 = 9  9
9  40
N = 90
40
N = 90
 = 3 cm
Volume of sphere =
= 3 cm
Volume of sphere = 

 (3)3 = 9
(3)3 = 9
Q80. A lead pencil consists of cylinder of wood with a solid cylinder of graphite fitted into it. The diameter of pencil is 7 mm. The diameter of graphite is 1 mm and length of pencil is 10 cm. Calculate the weight of the whole pencil in grams if the density of wood is 0.6 gm/cm3and of graphite 2.3 gm/cm3.
Solution
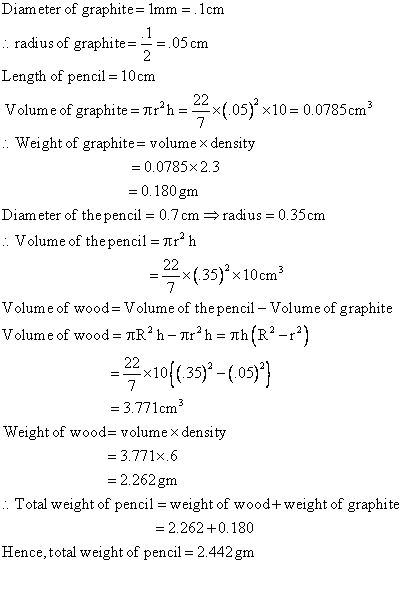
Q81. A bucket is 18 cm in diameter at the top and 6 cm in diameter at the bottom. If it is 8 cm high, find its capacity. Also, find the area of sheet used in making the bucket.
Solution
Here,
R = 9 cm
r = 3 cm
h = 8 cm
Capacity of the bucket
= 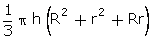
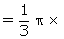 8 (92 + 32 + 9
8 (92 + 32 + 9  3 )
= 312
3 )
= 312  cm3
Area of the metallic sheet used in making the bucket
= Curved surface area of frustum +
cm3
Area of the metallic sheet used in making the bucket
= Curved surface area of frustum + 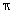 r2
=
r2
= 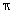 [ℓ (R + r)] +
[ℓ (R + r)] + 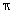 r2
=
r2
= 
 = 120
= 120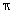 + 9
+ 9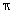 = 129
= 129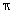 cm2
cm2

Q82. The
radius of the base and the height of a right circular cylinder are in the
ratio of 2: 3 and its volume is 1617 cu. cm. Find the curved surface area of
the cylinder. 
Solution
Let
the radius of the base of the cylinder be 2x and its height be 3x.
Volume of a cylinder = 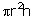
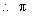 (2x)2 (3x) = 1617
(2x)2 (3x) = 1617
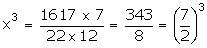
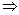 x =
x = 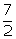 = 3.5 cm
= 3.5 cm
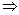 r = 7 cm, h = 10.5 cm
r = 7 cm, h = 10.5 cm
 Curved surface area of the cylinder = 2
Curved surface area of the cylinder = 2 rh
rh


Q83. Water
in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How
much area will it irrigate in 30 minutes, if 8 cm of standing water is
needed?
Solution
Consider
an area of cross section of canal be ABCD.
Area
of cross section = 6 × 1.5 = 9 m2
Speed
of water = 10 km/h = 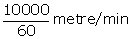 Volume
of water that flows in 1 minute from canal =
Volume
of water that flows in 1 minute from canal = 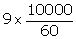 =1500m3
Volume
of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let
irrigated area be A. Volume of water irrigated in the required area will be
equal to the volume of water flowed in 30 minutes from canal.
Volume
of water that flows in 30 minutes from canal = Volume of water irrigated in
the required area
=1500m3
Volume
of water that flows in 30 minutes from canal = 30 × 1500 = 45000 m3
Let
irrigated area be A. Volume of water irrigated in the required area will be
equal to the volume of water flowed in 30 minutes from canal.
Volume
of water that flows in 30 minutes from canal = Volume of water irrigated in
the required area
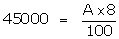 A
= 562500 m2
So,
area irrigated in 30 minutes is 562500 m2.
A
= 562500 m2
So,
area irrigated in 30 minutes is 562500 m2.
Q84. A shuttle cock used for playing badminton has the shape of a frustum of a cone mounted on a hemisphere. The external diameters of the frustum are 5 cm and 2 cm and the height of the entire shuttle cock is 7 cm. Find its external surface area.
Solution

Q85. The
internal and external radii of a hollow spherical shell are 3 cm and 5 cm
respectively. If it is melted to form a solid cylinder of height 10 cm, find the diameter of the cylinder.
cm, find the diameter of the cylinder.
Solution
Volume
of metal in spherical shell = 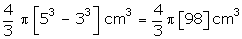 Let
r be the radius of solid cylinder.
The
spherical shell is melted to form a solid cylinder. So, their volume remains
the same.
Let
r be the radius of solid cylinder.
The
spherical shell is melted to form a solid cylinder. So, their volume remains
the same.

 Diameter of the solid cylinder = 7 cm
Diameter of the solid cylinder = 7 cm

Q86. Find the number of coins 1.5 cm in diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution
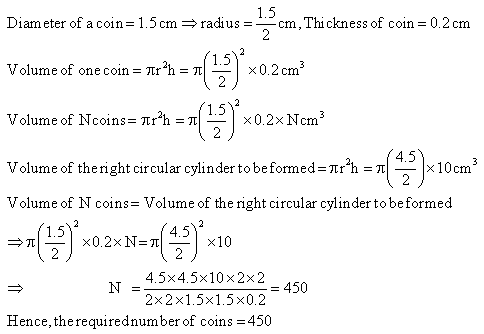
Q87. A copper rod of diameter 1 cm and length 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire.
Solution
Volume of the rod = 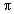 r2h
=
r2h
= 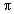
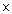

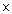 8 cm3
= 2
8 cm3
= 2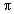 cm3
The length of the new wire of the same volume is = 18 m = 1800 cm
Volume of the wire = volume of the rod
cm3
The length of the new wire of the same volume is = 18 m = 1800 cm
Volume of the wire = volume of the rod
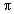 r2
r2 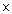 1800 = 2
1800 = 2 r2 =
r2 =  r =
r =  cm
So, the diameter of cross-section i.e. thickness of the wire is
cm
So, the diameter of cross-section i.e. thickness of the wire is  cm.
cm.

 r =
r =  cm
So, the diameter of cross-section i.e. thickness of the wire is
cm
So, the diameter of cross-section i.e. thickness of the wire is  cm.
cm.
Q88. The internal radii of the ends of a bucket, full of milk and of internal height 16 cm are 14 cm and 7 cm. If this milk is poured into a hemispherical vessel, find the internal diameter of the vessel.
Solution
 For bucket, h = 16 cm
r1 = 14 cm
r2 = 7 cm
V1 = Volume of bucket =
For bucket, h = 16 cm
r1 = 14 cm
r2 = 7 cm
V1 = Volume of bucket = 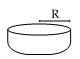 Let R cm be the radius of the hemispherical vessel
V2 = volume of vessel =
Let R cm be the radius of the hemispherical vessel
V2 = volume of vessel = 
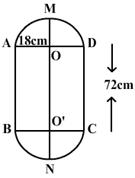
Q89. A cylindrical pipe has inner diameter of 4 cm and water flows through it at the rate of 20 m per minute. How long would it take to fill a conical tank, with diameter of base as 80 cm and depth 72 cm?
Solution
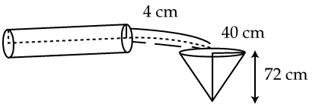 Let the time to fill the conical flask be x minutes.
In 1 minute, 20 m water flows.
So in x minutes, 20x m water will flow.
Let the time to fill the conical flask be x minutes.
In 1 minute, 20 m water flows.
So in x minutes, 20x m water will flow.
Comments
Post a Comment