Q1. Using section formula, show that the points
A(-3,-1), B(1,3) and C(-1,1) are collinear.
Solution
 Let
C(-1,1) divides AB in the ratio of k : 1
Using
section formula, we have:
(k
- 3)/(k + 1) = -1 … (1)
(3k
- 1)/(k + 1) = 1 … (2)
From
(1),
k
- 3 = -k - 1
2k
= 2
k
= 1
Thus,
C divides AB in the ratio 1: 1, that is, C is the mid-point of AB.
Let
C(-1,1) divides AB in the ratio of k : 1
Using
section formula, we have:
(k
- 3)/(k + 1) = -1 … (1)
(3k
- 1)/(k + 1) = 1 … (2)
From
(1),
k
- 3 = -k - 1
2k
= 2
k
= 1
Thus,
C divides AB in the ratio 1: 1, that is, C is the mid-point of AB.
Q2. Find the ratio in which the line joining points (1, 1) and (2, 4) is divided by the line 4x + y = 6.
Solution
Let the ratio be k:1.
The coordinates of the point dividing the line joining points (1, 1) and (2, 4) are
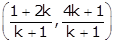 4x + y = 6 ... (i)
Put x =
4x + y = 6 ... (i)
Put x = 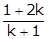 and y =
and y = 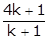 in (i)
in (i)
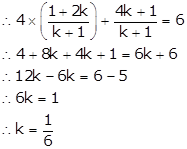 The ratio is 1:6.
The ratio is 1:6.
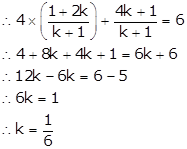 The ratio is 1:6.
The ratio is 1:6.
Q3. Find
the value of 's' if the point P(0,2) is equidistant from Q(3,s) and R(s,5).
Solution
PQ
= PR
PQ2
= PR2
(0
- 3)2 + (2 - s)2 =(0 - s)2 + (2 - 5)2
9
+ 4 - 4s + s2 = s2 + 9
4 = 4s
s = 1
Q4. Find the value of k if the area of a triangle is 16 sq. units and its vertices are (1, −2), (5, −6) and (k, 4).
Solution
Consider
x1 = 1, y1 = −2, x2 = 5, y2 = −6, x3 = k, y3 = 4
Area of the triangle = 16
x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2) = 0
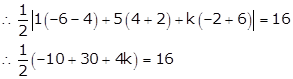 ∴ 4k + 20 = 32
∴ 4k=12
∴ k = 3
∴ 4k + 20 = 32
∴ 4k=12
∴ k = 3
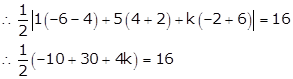 ∴ 4k + 20 = 32
∴ 4k=12
∴ k = 3
∴ 4k + 20 = 32
∴ 4k=12
∴ k = 3
Q5. If A (−2, 4), B (0, 0) and C (4, 2) are the vertices of ∆ABC, then find the length of the median through the vertex A.
Solution
Let AD be the median of ∆ABC.
D is the mid-point of BC.
The coordinates of D are 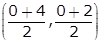 = (2, 1)
= (2, 1)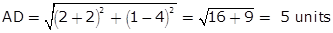
Q6. The three vertices of a parallelogram ABCD are A (−2, 3), B (6, 7), C (8, 3) and the fourth vertex D is
Solution
Let the fourth vertex be d(x, y). Then
Mid-point of AC = Mid-point of BD
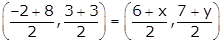
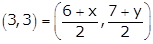
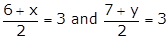 6 + x = 6 and 7 + y = 6
x = 0 and y = −1
6 + x = 6 and 7 + y = 6
x = 0 and y = −1
Q7. Two vertices of ∆ABC are given by A (6, 4) and B (−2, 2), and its centroid is G (3, 4). Find the coordinates of the third vertex C of ∆ABC.
Solution
Let the coordinates of C be (x, y).
According to the question,
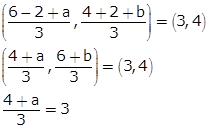 4 + a = 9
a = 5
Also,
4 + a = 9
a = 5
Also,
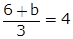 6 + b = 12
b = 6
The coordinates of C (5, 6).
6 + b = 12
b = 6
The coordinates of C (5, 6).
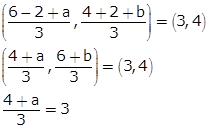 4 + a = 9
a = 5
Also,
4 + a = 9
a = 5
Also,
Q8. The line segment joining points (−3, −4) and (1, −2) is divided by the y-axis in the ratio
Solution
Let the y-axis divide the points in the ratio k: 1.Hence,
The coordinates of the point are
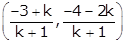 The y-axis divides the line. So, the x coordinate of a point is zero.
The y-axis divides the line. So, the x coordinate of a point is zero.
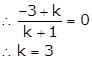 Hence, the ratio is 3:1.
Hence, the ratio is 3:1.
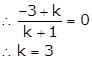 Hence, the ratio is 3:1.
Hence, the ratio is 3:1.
Q9. Find
the value of p so that the points with coordinates (3,5), (p,6) and  are collinear.
are collinear.
Solution
Let
the given points be A (3,5), B (p,6), C The
points will be collinear if ar (
The
points will be collinear if ar ( ABC) = 0
ar
(
ABC) = 0
ar
( ABC) =
ABC) = 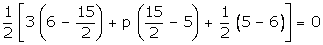
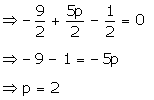
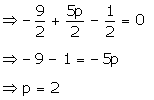
Q10. Find the coordinates of points which trisect the line segment joining (1, −2) and (−3, 4).
Solution
Let A (1, −2) and B (−3, 4) be the given points.Let the points of trisection be P and Q.
Then
AP = PQ = QB
AP:QB = 1:2 and AQ:QB = 2:1
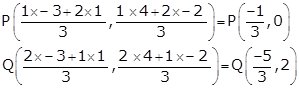
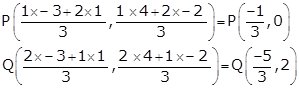
Q11. Show
that the point P(-4,2) lies on the line segment joining the points A(-4,6) and
B (-4,-6).
Solution
We
know, if points are collinear the area of the triangle formed by three points
as vertices is zero.
Area
= [-4 (6 + 6) - 4 (-6 - 2) - 4(2 - 6)] = 0
So,
the points are collinear.
Q12. 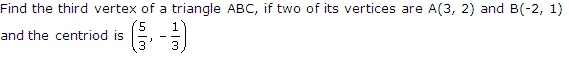
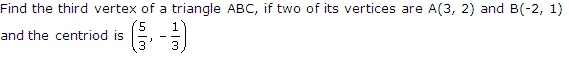
Solution

Q13. Find the ratio in which the line segment joining (8, 9) and (2, 6) is divided by the line 2x + y = 4.
Solution
Let the ratio be k:1.
The coordinates of the point dividing the line segment joining (8, 9) and (2, 6) are
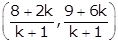 2x + y = 4 … (i)
Put x =
2x + y = 4 … (i)
Put x = 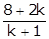 and y =
and y = 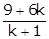 in (i)
in (i)
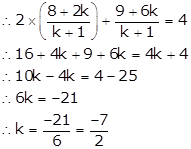 The ratio is 7:2
The ratio is 7:2
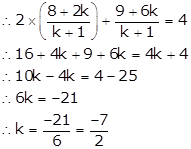 The ratio is 7:2
The ratio is 7:2
Q14. The
area of a triangle whose vertices are (-2, -2), (-1,-3) and (x, 0) is 3
square units. Find the value of x.
Solution
Area of triangle:
 (x1 (y2 - y3)
+ x2(y3 - y1) + x3 (y1
- y2)] = 3
(x1 (y2 - y3)
+ x2(y3 - y1) + x3 (y1
- y2)] = 3
 -2 (-3-0) -1 (0 + 2) + x(-2 + 3) = 6
-2 (-3-0) -1 (0 + 2) + x(-2 + 3) = 6
 6 - 2 + x = 6
6 - 2 + x = 6
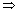 x = 2
x = 2
Q15. Points A (a, a), B (−a, −a) and C (0, 0) form the vertices of
Solution
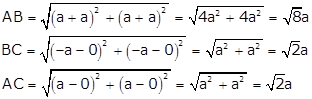 As BC = AC, ∆ABC is an isosceles triangle.
As BC = AC, ∆ABC is an isosceles triangle.
Q16. Find the perimeter of the triangle formed by the points (0,0), (1,0), (0,1).
Solution
By distance formula,
Distance Formula =  Let the points be A, B, C
AB =
Let the points be A, B, C
AB =  = 1 units
CA =
= 1 units
CA = 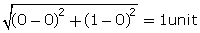 Similarly, BC =
Similarly, BC = 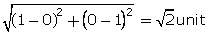
 Perimeter = (2 +
Perimeter = (2 + 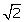 ) units
) units
 Let the points be A, B, C
AB =
Let the points be A, B, C
AB =
Q17. Find the ratio in which the line segment joining the points (3, 5) and (1, 4) is divided by the line 5x - y = 4.
Solution
Let the ratio be k:1.
The coordinates of the point dividing the line segment joining the points (3, 5) and (1, 4) are
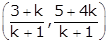 5x - y = 4 … (i)
Put x =
5x - y = 4 … (i)
Put x = 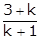 and y =
and y = 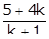 in (i)
in (i)
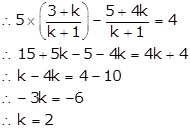 The ratio is 2:1.
The ratio is 2:1.
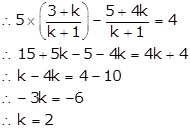 The ratio is 2:1.
The ratio is 2:1.
Q18. 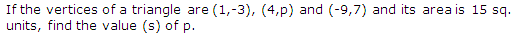
Solution
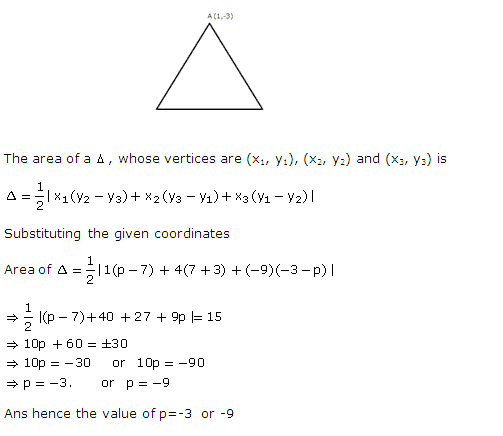
Q19. Determine
the ratio in which the line 3x + y - 9 = 0 divides the line segment joining
the points (1,3) and (2,7)
Solution
Let
the given line divides the line segment in ratio k:1 and point on line 3x + y
- 9 = 0 dividing line segment A(1,3) and B(2,7) be (a,b)
a
= 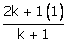 and b =
and b = 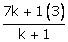
 And as point P (a,b) lies on straight line: 3x + y - 9 = 0
And as point P (a,b) lies on straight line: 3x + y - 9 = 0
 3a + b - 9 = 0
3a + b - 9 = 0
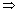
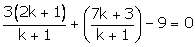
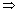 k =
k =  Required
ratio is 3:4.
Required
ratio is 3:4.
 And as point P (a,b) lies on straight line: 3x + y - 9 = 0
And as point P (a,b) lies on straight line: 3x + y - 9 = 0
Q20. Prove that the points (a,0), (0,b) and (1,1) are collinear if, 
Solution
Points A(a,0), B(0,b) and C(1,1) are collinear,  Area of
Area of  ABC = 0
ABC = 0
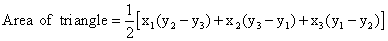 Here, x1 = a, y1 = 0; x2 = 0, y2 = b; x3 = 1, y3 = 1
Here, x1 = a, y1 = 0; x2 = 0, y2 = b; x3 = 1, y3 = 1
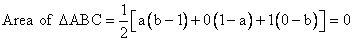
 ab - a - b = 0
ab - a - b = 0
 ab = a + b
ab = a + b
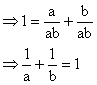
Q21. Find the area of the triangle whose vertices are (a, b), (a + b, a + b) and (a - b, a - b).
Solution
Consider x1 = a, y1 = b, x2 = a + b, y2 = a + b, x3 = a - b, y3 = a - b
According to the question,
Area of the triangle = x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)
= a [a + b - (a - b)] + (a + b)(a - b - b) + (a - b) (b - a - b)
= a [a + b - a + b] + (a + b)(a - 2b) + (a - b) (-a)
= 0
Q22. Find the coordinates of the point of intersection of the medians of triangle ABC; given A(-2, 3), B(6, 7) and C(4, 1).
Solution
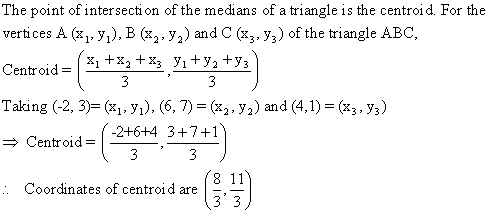
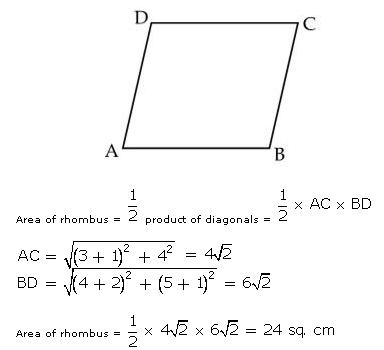
Q23. Find the area of the rhombus ABCD whose vertices are A(3,0), B(4,5), C(-1,4) and D(-2,-1).
Solution
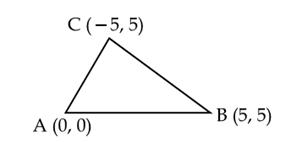
Q24. Prove
that the points (0, 0), (5, 5) and (-5, 5) are the vertices of a right angled
isosceles triangle.
Solution
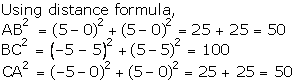
Q25. Find the area of a triangle whose vertices are (4, 12), (3, 9) and (0, 0).
Solution
Consider x1 = 1, y1 = 2, x2 = −5, y2 = 6, x3 = a, y3 = −2
According to the question,
Area of the triangle =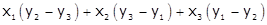 =
= 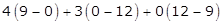 = 36 - 36
= 0
= 36 - 36
= 0
Q26. 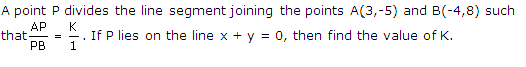
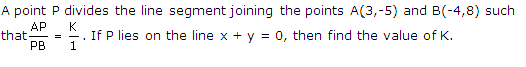
Solution
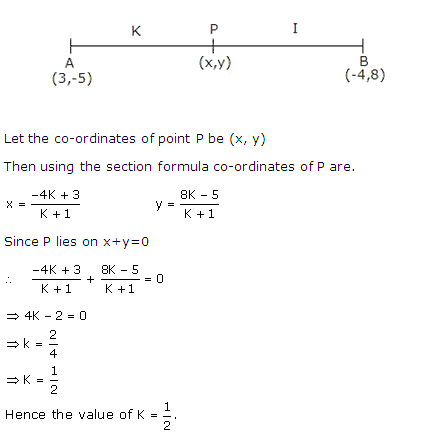
Q27. Find the area of the triangle whose sides are 17 cm, 25 cm and 26 cm.
Solution
Consider a = 17 cm, b = 25 cm, c = 26 cm
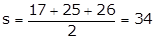 Area of the triangle =
Area of the triangle =  =
= 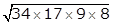 = 204 cm2
= 204 cm2
Q28. Three consecutive vertices of a
parallelogram ABCD are A(1,2), B(1,0) and C(4,0). Find the fourth vertex D.
Solution
Let
the co-ordinates of the fourth vertex D be (x, y).
We
know that diagonals of a parallelogram bisect each other.
 Mid-point
of BD = Mid-point of AC
Coordinates
of the mid-point of BD are
Mid-point
of BD = Mid-point of AC
Coordinates
of the mid-point of BD are  Coordinates
of the mid-point of AC are
Coordinates
of the mid-point of AC are 
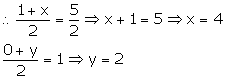 Thus,
the co-ordinates of the vertex D are (4, 2).
Thus,
the co-ordinates of the vertex D are (4, 2).
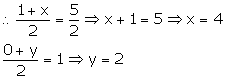 Thus,
the co-ordinates of the vertex D are (4, 2).
Thus,
the co-ordinates of the vertex D are (4, 2).
Q29. If the
points A(4,3) and B(x, 5) are on the circle with centre O(2,3); find the
value of x.
Solution
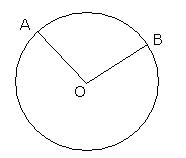 OA
= OB (Radii of same circle)
OA2
= OB2
OA
= OB (Radii of same circle)
OA2
= OB2
Q30. The mid points D, E, F of the sides AB, BC, CA of a triangle ABC are (1, 2), (3, -1) and (5, 0). Find the coordinates of the vertices A, B, C of the triangle.
Solution

Q31. If the point (k, 4) lies on a circle whose centre is at the origin and radius is 5, then k =
Solution
Let O (0, 0) be the origin and A (k, 4) be the point on the circle.OQ = 5OQ2 = 25(0 - k)2 + (0 - 4)2 = 25k2 + 16 = 25k2 = 9k = ±3
Q32. 

Solution

Q33. If the point P(x, y) is equidistant from the points A(5, 1) and B(-1, 5), then prove that 3x = 2y.
Solution

Q34. Find
the value of x such that PQ = QR, where P, Q and R are the points (2, 5) (x,
-3) and (7, 9) respectively.
Solution
PQ
= QR
 PQ2 = QR2
By
distance formula,
(x
- 2)2 + (-3 - 5)2 = (7 - x)2 + (9 + 3)2
x2
- 4x + 4 + 64 = 49 + x2 - 14x + 144
10x
= 193 - 68 = 125
x
= 12.5
PQ2 = QR2
By
distance formula,
(x
- 2)2 + (-3 - 5)2 = (7 - x)2 + (9 + 3)2
x2
- 4x + 4 + 64 = 49 + x2 - 14x + 144
10x
= 193 - 68 = 125
x
= 12.5
Q35. Show
that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.
Solution
Let
the given points be A (a, b + c), B (b, c + a), C (c, a + b).
These
points will be collinear if the area of triangle ABC is 0.
Now,
area ( ABC) =
ABC) = 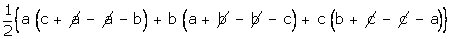
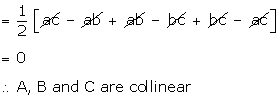
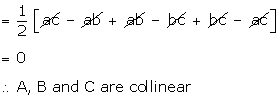
Q36. Find the area of the triangle whose sides are 13 cm, 15 cm and 10 cm.
Solution
Consider a = 13 cm, b = 15 cm, c = 10 cm
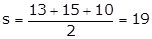 Area of the triangle =
Area of the triangle =
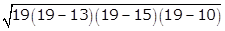 =
=  = 64.06 cm2
= 64.06 cm2
Q37. Find the ratio in which the line segment joining the points (1, -3) and (- 4, 5) is divided by the x-axis.
Solution

Q38. Show that the quadrilateral ABCD with A(3, 1), B(0, -2), C(1, 1) and D(4, 4) is a parallelogram.
Solution
Using the distance formula, we have
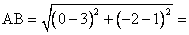

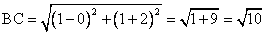
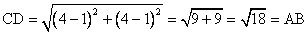
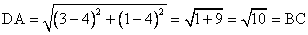
 AB = CD and BC = DA
Since, the opposite sides of a quadrilateral are equal, it is a parallelogram.
Hence, ABCD is a parallelogram.
AB = CD and BC = DA
Since, the opposite sides of a quadrilateral are equal, it is a parallelogram.
Hence, ABCD is a parallelogram.
Q39. If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p.
Solution

Q40. The ratio in which the line joining (1, 4) and (6, −4) is divided by the y-axis is
Solution
Let point C divide the y-axis in the ratio k:1.
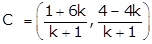 According to the question, x coordinate of C is zero.
According to the question, x coordinate of C is zero.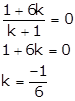 So, the ratio is 1:6.
So, the ratio is 1:6.
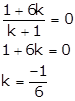 So, the ratio is 1:6.
So, the ratio is 1:6.
Q41. Find
the coordinates of the point B, if the point P(-4,1) divides the line segment joining the points A(2,-2) and
B in the ratio 3 : 5.
Solution
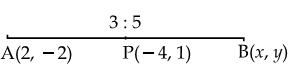 Let
coordinates of point B be (x,y)
By
section formula,
-4
=
Let
coordinates of point B be (x,y)
By
section formula,
-4
=
Q42. The
base BC of an equilateral ABC lies on y-axis. The co-ordinates of the point C
are (0,-3). If origin is the mid-point of BC, find the coordinates of point A
and B.
Solution
Let
(x, y) be the coordinates of point B.
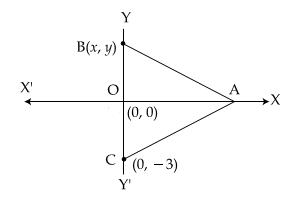 Using mid-point formula, we have:
Using mid-point formula, we have:
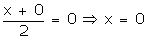
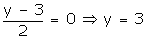
 Coordinates of B are (0, 3)
Coordinates of B are (0, 3)
 BC = 6 units
Now,
ABC is an equilateral triangle and OB = 3 units, AB = 6 units
BC = 6 units
Now,
ABC is an equilateral triangle and OB = 3 units, AB = 6 units
 AO2 = 62 - 32
= 27
AO2 = 62 - 32
= 27  AO = 3
AO = 3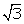 units
units
 Coordinates of A are
Coordinates of A are 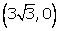
 Using mid-point formula, we have:
Using mid-point formula, we have:
Q43. Find the point which divides the line segment joining the two points (6, 3) and (−4, 5) internally in the ratio 3:2.
Solution
Section Formula:
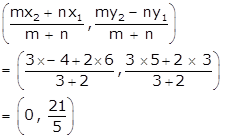
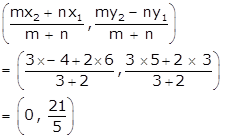
Q44. In the seating arrangement of desks in a class room three students Rohini, Sandhya and Bina are seated at A(3, 1), B(6, 4) and C(8, 6). Do you think they are seated in a line?
Solution
If three students are seated in a line, then AB + BC = AC or AB + AC = BC or AC + BC = AB
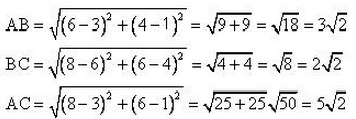
 AB + BC = CA
Hence, the three places are in line.
Yes, the three students are sitting in a line.
AB + BC = CA
Hence, the three places are in line.
Yes, the three students are sitting in a line.
 AB + BC = CA
Hence, the three places are in line.
Yes, the three students are sitting in a line.
AB + BC = CA
Hence, the three places are in line.
Yes, the three students are sitting in a line.
Q45. The points A(2,9), B(a,5) and C(5,5) are
the vertices of a triangle ABC, right angled at B. Find the value of a and
hence the area of triangle ABC.
Solution
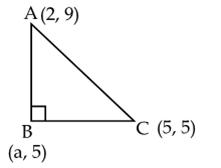 Since,
ABC is a right triangle, right angled at B, we have:
AB2
+ BC2 = CA2
[(2
- a)2 + (9 - 5)2] + [(a - 5)2 + (5 - 5)2]
= (2 - 5)2 + (9 - 5)2
4
+ a2 - 4a + 16 + a2 + 25 - 10a = 9 + 16
2a2
- 14a + 20 = 0
a2
- 7a + 10 = 0
(a
- 5)(a - 2) = 0
a
= 5 or 2
But
a cannot be 5 as then the points B and C will coincide.
Since,
ABC is a right triangle, right angled at B, we have:
AB2
+ BC2 = CA2
[(2
- a)2 + (9 - 5)2] + [(a - 5)2 + (5 - 5)2]
= (2 - 5)2 + (9 - 5)2
4
+ a2 - 4a + 16 + a2 + 25 - 10a = 9 + 16
2a2
- 14a + 20 = 0
a2
- 7a + 10 = 0
(a
- 5)(a - 2) = 0
a
= 5 or 2
But
a cannot be 5 as then the points B and C will coincide.
Q46. Show
that the points (-4,0), (4,0) and (0,3) are vertices of an isosceles
triangle.
Solution
Let
A (-4,0), B (4,0), C(0,3) be the given points.
AB2
= 82 = 64  AB = 8 units
BC
=
AB = 8 units
BC
= 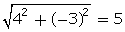 units
CA
=
units
CA
=  units
units
 BC = AC
BC = AC 
 ABC is isosceles
ABC is isosceles
Q47. Find points on the x-axis, which are at a distance of 5 units from the point A(5,-3).
Solution
Let the required point on x-axis be (x, 0).
Using distance formula, we have:
(x - 5)2 + (0 + 3)2 = (5)2
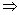 (x - 5)2 = 25 - 9 =
(x - 5)2 = 25 - 9 = 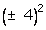
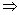 x - 5 =
x - 5 = 
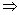 x = 9, 1
x = 9, 1
 Required points on x-axis are (9, 0) and (1, 0).
Required points on x-axis are (9, 0) and (1, 0).
Q48. Find the ratio in which the line 3x + y – 9 = 0 divides the line segment joining the points (1,3) and (2,7).
Solution
Let the line 3x + y – 9 = 0 divide the line segment joining the points A(1,3) and B(2,7) at the point C in the ratio k:1
Then point C by section formula is
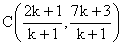 As C lies on the line3x + y – 9 = 0, we have
As C lies on the line3x + y – 9 = 0, we have

 6k + 3 + 7k + 3 - 9k - 9 = 0
6k + 3 + 7k + 3 - 9k - 9 = 0
 4k - 3 = 0
4k - 3 = 0
 The required ratio is 3:4 internally
The required ratio is 3:4 internally
Q49. Find the values of y, if the distance between the points (2, -3) and (10, y) is 10 units.
Solution

Q50. 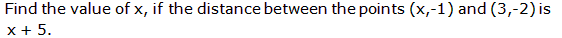
Solution

Q51. Find the point on the X-axis which is equidistant from (2, -5) and (-2, 9).
Solution
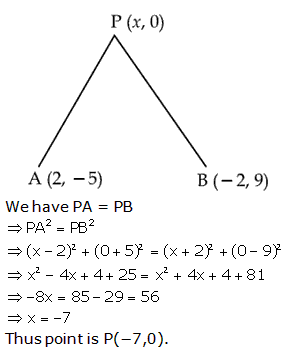
Q52. If A(3,0), B(4,5), C(-1,4) and D(-2,-1) be four points in a plane, show that ABCD is a rhombus but not a square.
Solution
The given points are A(3,0), B(4,5), C(-1,4) and D(-2,-1).
Using distance formula,
AB = 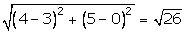 BC =
BC =  CD =
CD = 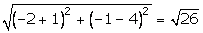 DA =
DA = 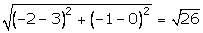 AC =
AC = 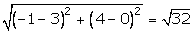 BD =
BD = 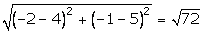 Since, AB = BC = CD = DA and AC
Since, AB = BC = CD = DA and AC 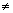 BD,
Hence, ABCD is a rhombus but not a square.
BD,
Hence, ABCD is a rhombus but not a square.
Q53. 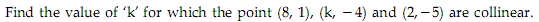
Solution
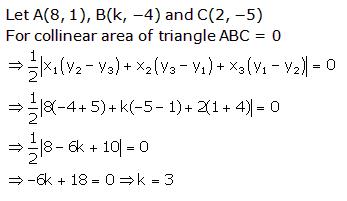
Q54. If three points A (0, 0), B (3,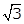 ) and C (3, k) form an equilateral triangle, then k =
) and C (3, k) form an equilateral triangle, then k =
Solution
According to the question,AB = BC = ACAB = AC∴ AB2 = AC2∴ (0 - 3)2 + (0 ⎼ 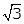 )2 = (0 ⎼ 3)2 + (0 ⎼ k)2 ∴ 9 + 3 = 9 + k2∴ k2 = 3∴ k =
)2 = (0 ⎼ 3)2 + (0 ⎼ k)2 ∴ 9 + 3 = 9 + k2∴ k2 = 3∴ k =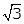
Q55. Find a relation between x and y if the points (x,y), (1,2) and (7,0) are collinear.
Solution
Points A (x,y), B (1,2) and C(7,0) will be collinear if the area of the triangle formed by these points is zero.
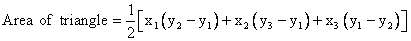 Here x1 = x, y1 = y, x2 = 1, y2 = 2, x3 = 7, y3 = 0
Substituting the values, Area of
Here x1 = x, y1 = y, x2 = 1, y2 = 2, x3 = 7, y3 = 0
Substituting the values, Area of  ABC = 2x + 6y -14
Now area of
ABC = 2x + 6y -14
Now area of  ABC = 0
ABC = 0
 2x + 6y -14 = 0
2x + 6y -14 = 0
 x + 3y = 7
x + 3y = 7
 ABC = 2x + 6y -14
Now area of
ABC = 2x + 6y -14
Now area of  ABC = 0
ABC = 0
Q56. Show that the point P(0,-2), Q(3,1), R(0,4)
and S(-3,1) are the vertices of a square PQRS.
Solution
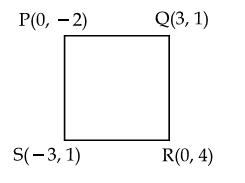 Using
distance formula,
PQ
=
Using
distance formula,
PQ
=
Q57. The points A(3, 2) and B(2, -3) are equidistant from a point P(x, y). Find the relation between x and y.
Solution
Given: A(3, 2) and B(2, -3) are equidistant from the point P(x, y)
Then, PA = PB
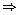 PA2 = PB2
(x - 3)2 + (y - 2)2 = (x - 2)2 + (y + 3)2
PA2 = PB2
(x - 3)2 + (y - 2)2 = (x - 2)2 + (y + 3)2
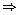 x2 + 9 - 6x + y2 + 4 - 4y = x2 + 4 - 4x + y2 + 9 + 6y
x2 + 9 - 6x + y2 + 4 - 4y = x2 + 4 - 4x + y2 + 9 + 6y
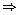 -6x - 4y = -4x + 6y
-6x - 4y = -4x + 6y
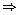 -2x - 10y = 0
-2x - 10y = 0
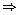 x + 5y = 0
x + 5y = 0
Q58. The
midpoint of the line segment joining points A(x,y + 1) and B(x + 1, y + 2) is
C. Find the value of x and y if the coordinates of C are (3/2, 5/2).
Solution
The
midpoint of two points (x1,y1) and (x2,t2)
is ( 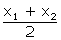 ,
,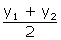 )
Hence
midpoint of A and B is C[(x1 + x2)/2, (y1 +
y2)/2]
(x1 + x2)/2 = 3/2
)
Hence
midpoint of A and B is C[(x1 + x2)/2, (y1 +
y2)/2]
(x1 + x2)/2 = 3/2
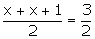 2x
= 3 - 1
x
= 1
Similarly,
2x
= 3 - 1
x
= 1
Similarly,
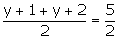 2y + 3 = 5
2y = 2
2y + 3 = 5
2y = 2
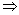 y = 1
Coordinates
of midpoint (1,1)
y = 1
Coordinates
of midpoint (1,1)
Q59. Find
the points on the x-axis which are at a distance of 2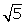 units from the point (7, -4). How many such points
are there?
units from the point (7, -4). How many such points
are there?
Solution
Let
the point on x-axis be P(x, 0). Let the given point be Q = (7, -4).
PQ
= 2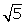 Using
distance formula,
PQ2
= (x - 7)2 + (0 + 4)2 = (2
Using
distance formula,
PQ2
= (x - 7)2 + (0 + 4)2 = (2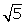 )2
x2
- 14x + 49 + 16 = 20
x2
- 14x + 45 = 0
(x
- 9) (x - 5) = 0
x
= 9, 5
Hence,
there are two such points, (9, 0) and (5, 0).
)2
x2
- 14x + 49 + 16 = 20
x2
- 14x + 45 = 0
(x
- 9) (x - 5) = 0
x
= 9, 5
Hence,
there are two such points, (9, 0) and (5, 0).
Q60. Find the co-ordinates of a point A, where AB is the diameter of a circle whose centre is (2,-3) and B is (1, 4).
Solution
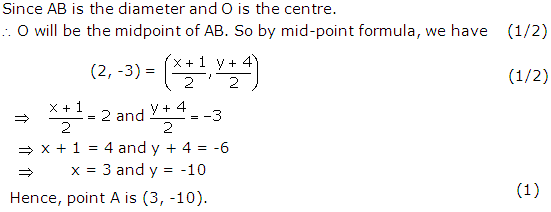
Q61. In the
figure, in  ABC, D and E are the mid-points of the sides BC and
AC respectively. Find the length of
DE. Prove that DE =
ABC, D and E are the mid-points of the sides BC and
AC respectively. Find the length of
DE. Prove that DE =  AB.
AB.
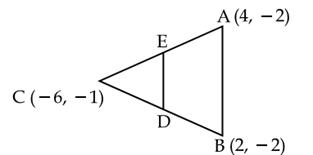

Solution
Coordinates
of E = 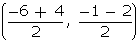 =
= 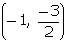 Coordinates
of D =
Coordinates
of D = 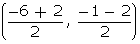 =
= 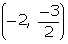 DE
=
DE
= 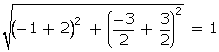 AB
=
AB
= 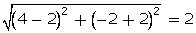 Hence,
DE =
Hence,
DE =  AB
AB
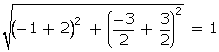 AB
=
AB
=
Q62. Find
the point on x-axis which is equidistant from the points (-2,5) and (2,-3).
Solution
 Let
the point on x-axis be (a,0)
Since
PA = PB
Let
the point on x-axis be (a,0)
Since
PA = PB
Q63. If A(1, 2), B(4, y), C(x, 6) and D(3, 5) are the vertices of a parallelogram ABCD taken in order, find the values of x and y.
Solution

Q64. Show that the points A (a, b+c), B (b, c + a) and C (c, a + b) are collinear.
Solution
If the given points are collinear then the area of the triangle formed by joining these points is zero.
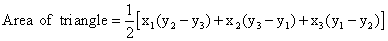 Here, x1 = a, y1 = b + c; x2 = b, y2 = c + a; x3 = c, y3 = a + b.
Substituting the values in the formula for area of a triangle, you get
Here, x1 = a, y1 = b + c; x2 = b, y2 = c + a; x3 = c, y3 = a + b.
Substituting the values in the formula for area of a triangle, you get

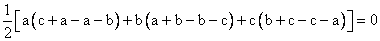
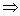

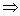 ac - ab + ab - bc + bc - ac = 0
Hence the given points are collinear.
ac - ab + ab - bc + bc - ac = 0
Hence the given points are collinear.
Q65. Find a point on y-axis which is equidistant
from (2,2) and (9,9).
Solution
Let
the required point on y-axis be (0, y).
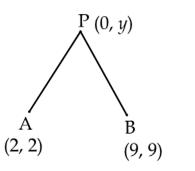 According
to question,
PA
= PB
PA2
= PB2
According
to question,
PA
= PB
PA2
= PB2

 - 4y + 8 =
- 4y + 8 =  - 18y + 162
14y
= 154
- 18y + 162
14y
= 154
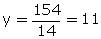 Thus,
the required point is (0, 11).
Thus,
the required point is (0, 11).
 According
to question,
PA
= PB
PA2
= PB2
According
to question,
PA
= PB
PA2
= PB2
Q66. Find the co-ordinates of a point A, where
AB is the diameter of circle whose centre is O (2, -3) and B is (1, 4).
Solution
Let
the co-ordinates of A be (x, y).
The
mid-point of AB is O.
Using
mid-point formula, we have:
(x
+ 1)/ 2 = 2 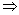 x = 3
(y
+ 4)/2 = -3
x = 3
(y
+ 4)/2 = -3 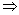 y = -10
y = -10
 Thus, the coordinates of point A are (3,
-10).
Thus, the coordinates of point A are (3,
-10).
Q67. Find the area of a quadrilateral whose vertices, taken in order, are (-4,-2), (-3,-5), (3,-2) and (2,3).
Solution
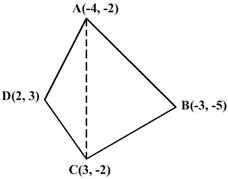 The vertices of the quadrilateral ABCD are A (-4, -2), B (-3, -5), C (3, -2) and D (2, 3).
Area of quad. ABCD = ar
The vertices of the quadrilateral ABCD are A (-4, -2), B (-3, -5), C (3, -2) and D (2, 3).
Area of quad. ABCD = ar
Q68. In
what ratio is the line segment joining the points P(-2,-3) and Q(3,7) divided
by y-axis?
Solution
The
coordinates of point on y-axis are (0, y).
Let
it divide the line segment joining (-2,-3) and (3,7) in ratio k : 1.
Using
section formula, we have:

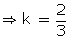 Thus,
the required ratio is 2: 3.
Thus,
the required ratio is 2: 3.
Q69. Find the co-ordinates of the circum-centre of the triangle ABC, whose vertices A, B and C are (4, 6), (0, 4) and (6, 2) respectively.
Solution

Q70. 

Solution

Q71. If A
and B are the points (-2,-2) and (2,-4) respectively, find the coordinates of
P on the line segment AB such that AP = 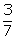 AB.
AB.
Solution
 Using section formula, we have:
Using section formula, we have:
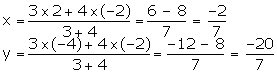


Comments
Post a Comment