Q1. Solve
the below equation by the perfect square method:
5x2 - 6x - 2 = 0
Solution
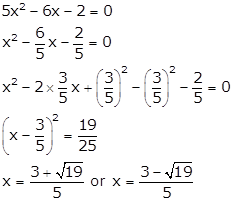
Q2. 

Solution

Q3. To
make 6x2 + 5x = 0 a perfect square, we need to add and subtract
Solution
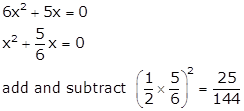
Q4. Solve
the below equation by the factorisation method:
x2 - 9x + 20 = 0
Solution
x2
- 9x + 20 = 0
x2 - 5x - 4x + 20 = 0
x(x - 5) - 4(x - 5) = 0
(x - 4)(x - 5) = 0
x = 4 or x = 5
Q5. Solve the following equation

Solution


Q6. Solve
the below equation by the perfect square method:
2x2
- 5x + 3 = 0
Solution
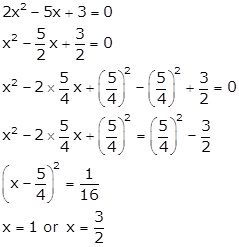
Q7. Find
the solution of the quadratic equation by the formula method.
x2 + 4x - 2 = 0
Solution
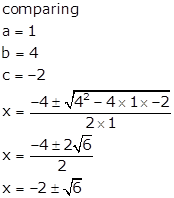
Q8. Form a quadratic equation whose roots are  and
and .
.
Solution
Sum of roots(S) =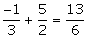 Product of roots (P) =
Product of roots (P) =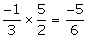 Required equation is x2-Sx+P=0
Required equation is x2-Sx+P=0
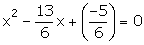 6x2 - 13x - 5=0
6x2 - 13x - 5=0
Q9. Solve
the quadratic equation by the completing the square method.
x2
+ 4x + 1 = 0
Solution
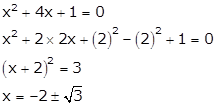
Q10. The sum of the reciprocals Rehman"s ages 3 years ago and five years from now is 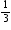 . Find his present age.
. Find his present age.
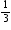 . Find his present age.
. Find his present age.Solution
Let Rehman"s present age = 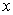 years
Rehman's age 3 years ago =
years
Rehman's age 3 years ago =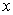 - 3 years
Five years from now =
- 3 years
Five years from now = 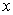 + 5 years
According to question
+ 5 years
According to question
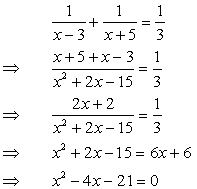
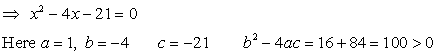
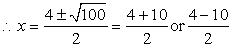
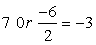 Rejecting negative value
Rejecting negative value 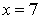 Hence Rehmans age =7 Yrs
Hence Rehmans age =7 Yrs
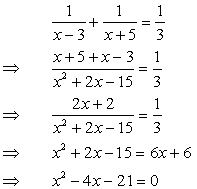
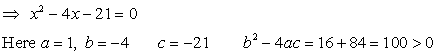
Q11. Solve
the quadratic equation by the formula method.
x2
+ 2x - 3 = 0
Solution
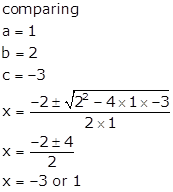
Q12. Find
the solution of the quadratic equation by the formula method.
x2
+ 7x + 12 = 0
Solution
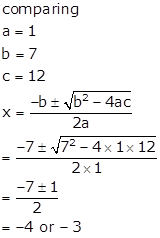
Q13. If 8 is a root of the equation x2 - 10x + k = 0, then the value of k is:
Solution
Given, 8 is a root of the equation x2 - 10x + k = 0.
(8)2 - 10(8) + k = 0
64 - 80 + k = 0
k = 16
Q14. One of the roots of the quadratic equation 6x2 - x - 2 = 0 is:
Solution
6x2 - x - 2 = 0
6x2 - 4x + 3x - 2 = 0
2x(3x - 2) + 1(3x - 2) = 0
(3x - 2) (2x + 1) = 0
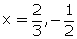 Thus, the required one root of the given quadratic equation is
Thus, the required one root of the given quadratic equation is 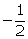 .
.
Q15. Solve the following quadratic equations by factorization :


Solution

Q16. Solve
the quadratic equation by the completing the square method.
x2 + 8x + 1 = 0
Solution

Q17. Solve for x:
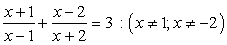
Solution
Consider equation
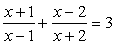
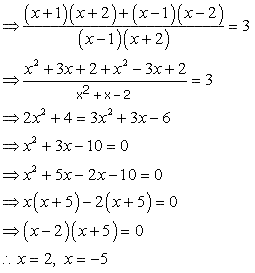
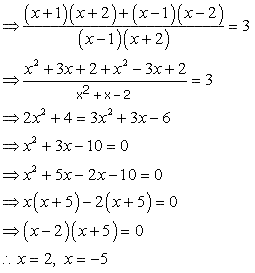
Q18. Solve
the quadratic equation by the formula method.
3x2
+ 9x - 2 = 0
Solution
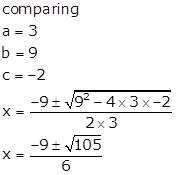
Q19. 

Solution

Q20. Find
the solution of the quadratic equation by the formula method.
x2 + 2x - 5 = 0
Solution
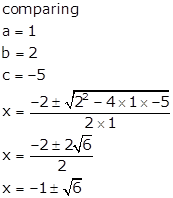
Q21. Solve the following quadratic equations by factorization :


Solution
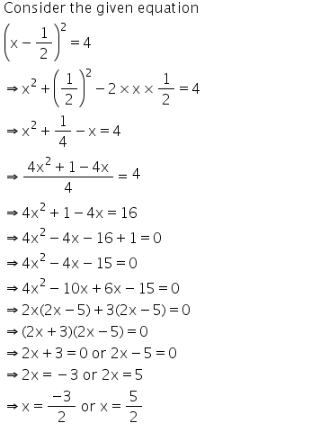
Q22. 

Solution

Q23. Solve the following quadratic equation by the factorisation method:
x2 + 2√2x - 6 = 0
Solution
x2 + 2√2x - 6 = 0
x2 + 3√2x - √2x - 6 = 0
x(x + 3√2) - √2(x + 3√2) = 0
(x + 3√2)(x - √2) = 0
Q24. A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more it would have taken 30 minutes less for the journey. Find the original speed of the train.
Solution
Let the original speed of train be 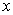 km/h.
then increased speed
km/h.
then increased speed 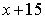 km/hr
usual time
km/hr
usual time  hours
New time
hours
New time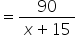 hours
According to the question
hours
According to the question
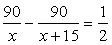

 Rejecting the negative value, we have x = 45
Hence usual speed of train = 45 km/hr.
Rejecting the negative value, we have x = 45
Hence usual speed of train = 45 km/hr.
 hours
New time
hours
New time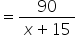 hours
According to the question
hours
According to the question

 Rejecting the negative value, we have x = 45
Hence usual speed of train = 45 km/hr.
Rejecting the negative value, we have x = 45
Hence usual speed of train = 45 km/hr.
Q25. Find the value of m so that the quadratic equation mx(x - 7) + 49 = 0 has two equal roots.
Solution
The given quadratic equation is mx(x-7)+49=0
mx2-7mx+49=0
a = m, b = -7m and c = 49
It is given that the roots of this equation are equal.
 D = b2 - 4ac=0
(-7m)2 - 4(m)(49)=0
49m2 - 4(m)(49)=0
49m(m-4)=0
49m=0 or m - 4 = 0
m = 0 or m=4
For m = 0 equation will not be quadratic.
Hence the value of m = 4.
D = b2 - 4ac=0
(-7m)2 - 4(m)(49)=0
49m2 - 4(m)(49)=0
49m(m-4)=0
49m=0 or m - 4 = 0
m = 0 or m=4
For m = 0 equation will not be quadratic.
Hence the value of m = 4.
Q26. The
speed of a boat in still water is 11 km/hr. It can go 12 km upstream and
return downstream to the original point in 2hrs 45 min. Find the speed of the
stream.
Solution
Let
the speed of the stream = x km/hr
Speed
of the boat in still water = 11 km/hr
Speed
of the boat downstream = (11 + x) km/hr
Speed
of the boat upstream = (11 - x) km/hr
According
to the given information,
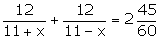
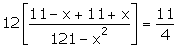
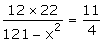 121
- x2 = 96
x2
= 25
x
=
121
- x2 = 96
x2
= 25
x
= 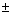 5
Rejecting
negative value, as speed cannot be negative. So, x = 5.
Hence,
the speed of the stream is 5 km/hr.
5
Rejecting
negative value, as speed cannot be negative. So, x = 5.
Hence,
the speed of the stream is 5 km/hr.
Q27. A person on tour has Rs. 306 for his daily expenses. If he extends his tour for four days, he has to cut down his daily expenses by Rs. 3. Find the original duration of the tour.
Solution
Let original duration of tour be x days
Daily expenses initially= 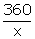 Daily expenses later =
Daily expenses later = 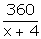 Accordingly,
Accordingly,
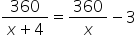
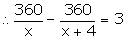 360
360  4 = 3(x(x + 4))
4 = 3(x(x + 4))
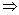 x2 + 4x - 480 = 0
x2 + 4x - 480 = 0
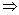 (x + 24) (x - 20) = 0
(x + 24) (x - 20) = 0
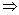 x = -24 or x = 20
X = -24 not possible
x = -24 or x = 20
X = -24 not possible
 x = 20
x = 20
 Original duration of tour = 20 days
Original duration of tour = 20 days
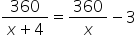
Q28. Solve by method of completing square.
by method of completing square.
Solution
The coefficient of 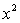 is not perfect square. So we divide the equation through out by 3
is not perfect square. So we divide the equation through out by 3
 divide and multiply coefficient of
divide and multiply coefficient of 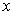 by 2
by 2
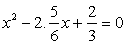 Add and subtract
Add and subtract  to the above equation, we have,
to the above equation, we have,
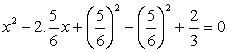
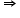
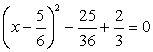
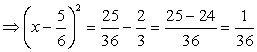

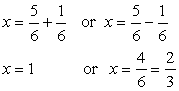 Required solution =1,
Required solution =1,
 to the above equation, we have,
to the above equation, we have,
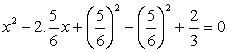
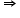
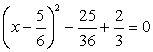
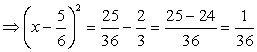

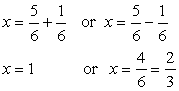 Required solution =1,
Required solution =1,
Q29. (2x - y)2 =
Solution
(2x - y)2 = 4x2
- 4xy + y2
Q30. Using quadratic formula solve for 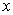
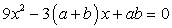
Solution
 Here A = 9 B = -3(a + b) C = a b
Using quadratic formula, we have
Here A = 9 B = -3(a + b) C = a b
Using quadratic formula, we have
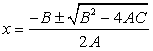

Q31. The positive root of 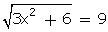 is:
is:
Solution
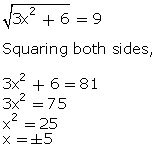 Thus, the positive root of the given equation is 5.
Thus, the positive root of the given equation is 5.
Q32. A plane left 30 minutes late then its scheduled time and in order to reach the destination 1500 km away in time it had to increase the speed by 250 km/h from the usual speed. Find its usual speed.
Solution
Let usual speed of plane=x km/hr
Usual time taken=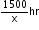 Increased speed
Increased speed 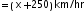 New time=
New time=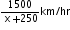 According to question,
According to question,


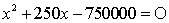 By factorisation method,
By factorisation method,

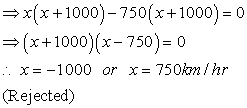 x = -1000 , because speed can't be negative.
Hence, usual speed of plane is 750 km/hr.
x = -1000 , because speed can't be negative.
Hence, usual speed of plane is 750 km/hr.
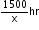 Increased speed
Increased speed 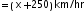 New time=
New time=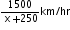 According to question,
According to question,

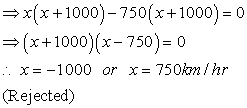 x = -1000 , because speed can't be negative.
Hence, usual speed of plane is 750 km/hr.
x = -1000 , because speed can't be negative.
Hence, usual speed of plane is 750 km/hr.
Q33. Solve
the quadratic equation by the completing the square method.
x2
+ x - 6 = 0
Solution
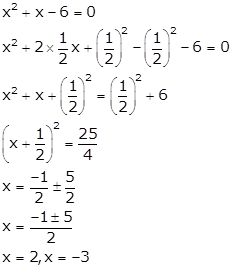
Q34. Using Quadratic formula ,solve the following quadratic equation

Solution
Comparing this equation with 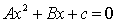 we have
we have
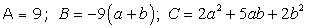
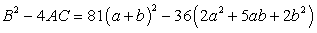 =
=  =
=  =
=  =
=  So the given roots of the given equation are real and given by
So the given roots of the given equation are real and given by

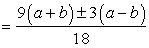


 =
=  =
=  =
=  So the given roots of the given equation are real and given by
So the given roots of the given equation are real and given by


Q35. Find the roots of the equation
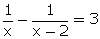 , x
, x 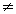 0,
0,
Solution

Q36. Find
two positive numbers whose squares have the difference 48 and the sum of the
numbers is 12.
Solution
Since
sum of the numbers is 12, the two numbers are x and 12 - x.
By
question,
x2
- (12 - x)2=48
x2
- 144 - x2 + 24x = 48
24x
= 144 + 48
x
= 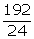 = 8
The
two numbers are 8 and 4.
= 8
The
two numbers are 8 and 4.
Q37. Solve  by factorization method.
by factorization method.
 by factorization method.
by factorization method.
Solution

Q38. 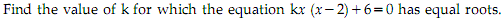
Solution
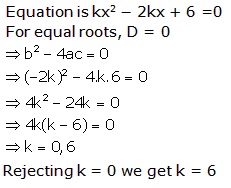
Q39. Solve for x:
6x2 + 7x - 10 = 0
Solution
6x2 + 7x - 10 = 0
6x2 + 12x - 5x - 10 = 0
6x(x + 2) - 5(x + 2) = 0
(6x - 5)(x + 2) = 0
x = -2, 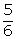
Q40. Find two consecutive positive integers, sum of whose squares is 365.
Solution
Let two consecutive positive integers be 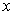 and
and 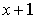 .
According to the question,
.
According to the question,
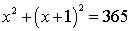
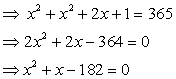 By factorisation method, we get
By factorisation method, we get

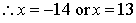 Since the integers are positive.
x = -14 is not acceptable.
Hence, the required positive integers 3 and 14.
Since the integers are positive.
x = -14 is not acceptable.
Hence, the required positive integers 3 and 14.
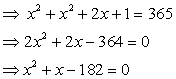 By factorisation method, we get
By factorisation method, we get

Q41. 

Solution

Q42. Find the roots of the quadratic equation: a2b2x2 + b2x - a2x - 1 = 0.
Solution
a2b2x2 + b2x - a2x - 1 = 0
b2x(a2x + 1) - 1(a2x + 1) = 0
(b2x - 1) (a2x + 1) = 0
x = 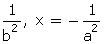
Q43. The sum of the reciprocals of Rehman's ages
(in years) 3 years ago and 5 years from now is 1/3. Find his present age.
Solution
Let
the present age of Rehman be x years.
So,
3 years ago Rehman's age = (x - 3) years
And
5 years hence, Rehman's age = (x + 5)
years
According
to question, we have:
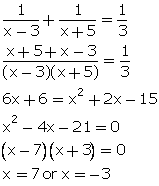 But
x, being the age cannot be negative. So, x = 7.
Thus,
the present age of Rehman is 7 years.
But
x, being the age cannot be negative. So, x = 7.
Thus,
the present age of Rehman is 7 years.
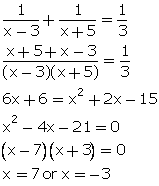 But
x, being the age cannot be negative. So, x = 7.
Thus,
the present age of Rehman is 7 years.
But
x, being the age cannot be negative. So, x = 7.
Thus,
the present age of Rehman is 7 years.
Q44. Which of the following equations has two distinct real roots?
Solution
A quadratic equation has two distinct roots if D = b2 - 4ac > 0.
Consider the quadratic equation x2 + x - 5 = 0.
Here, D = (1)2 - 4(1)(-5) = 1 + 20 = 21 > 0
Thus, this equation has two distinct real roots.
Q45. Find two numbers whose sum is 27 and product is 182.
Solution
Let first number be x then second number be 27 - x.
According to question,
x(27 - x) = 182
27x - x2 = 182
x2 + 27x +182 = 0
 x2 -14x - 13x + 182 = 0
x2 -14x - 13x + 182 = 0
 x(x - 14) - 13(x - 14) = 0
x(x - 14) - 13(x - 14) = 0
 (x - 14)(x - 13) = 0
(x - 14)(x - 13) = 0
 x = 14 or x = 13
Hence the required numbers are 13 and 14.
x = 14 or x = 13
Hence the required numbers are 13 and 14.
 x2 -14x - 13x + 182 = 0
x2 -14x - 13x + 182 = 0
 x(x - 14) - 13(x - 14) = 0
x(x - 14) - 13(x - 14) = 0
 (x - 14)(x - 13) = 0
(x - 14)(x - 13) = 0
 x = 14 or x = 13
Hence the required numbers are 13 and 14.
x = 14 or x = 13
Hence the required numbers are 13 and 14.
Q46. Find
the solution of the quadratic equation by the formula method.
x2 + 5x - 10 = 0
Solution
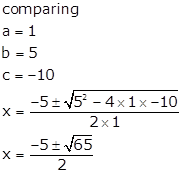
Q47. 

Solution

Q48. The product of Tanay's age (in years) five years ago and his age ten years later is 16. Determine Tanay's present age.
Solution
Let the present age of Tanay be x years.
Then, from the given information, we have:
(x - 5) (x + 10) = 16
x2 + 5x - 50 = 16
x2 + 5x - 66 = 0
x2 - 6x +11x - 66 = 0
x(x - 6) +11(x - 6) =0
(x - 6)(x +11) = 0
x = -11 or 6
Rejecting x = -11, as age cannot be negative.
 Present age of Tanay is 6 years
Present age of Tanay is 6 years
Q49. Two
water taps together can fill a tank in 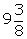 hours. The tap
of larger diameter takes 10 hours less than the smaller one to fill the tank
separately. Find the time in which each tap can separately fill the tank.
hours. The tap
of larger diameter takes 10 hours less than the smaller one to fill the tank
separately. Find the time in which each tap can separately fill the tank.
Solution
Let
the larger tap can fill the tank in x hours.
Then,
the smaller tap will fill the tank in (x + 10) hours.

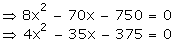
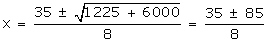 = 15 (rejecting negative value)
= 15 (rejecting negative value)
 Larger tap can fill the tank in 15 hours
Smaller tap can fill the tank in 25 hours
Larger tap can fill the tank in 15 hours
Smaller tap can fill the tank in 25 hours

Q50. A motor boat whose speed is 36 km/h in still water takes 1 hour more to go 48 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution
Let the speed of the stream be 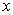 km/h
Therefore speed of boat upstream =
km/h
Therefore speed of boat upstream = And speed of boat in downstream
And speed of boat in downstream 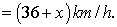 Time taken to go upstream
Time taken to go upstream 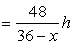 “ “ “ downstream
“ “ “ downstream 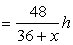 According to question
According to question
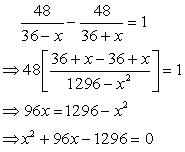 Using the quadratic formula.
Using the quadratic formula.
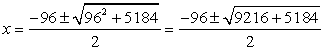
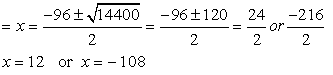 Since
Since 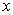 is the speed of stream, it cannot be negative so we ignore the root
is the speed of stream, it cannot be negative so we ignore the root 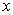 = - 108. Therefore
= - 108. Therefore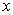 = 12 gives the speed of stream as 12 Km/Hr
= 12 gives the speed of stream as 12 Km/Hr
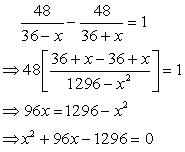 Using the quadratic formula.
Using the quadratic formula.
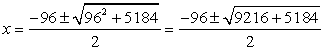
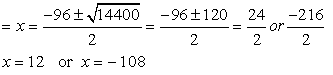 Since
Since
Q51. The
product of the digits of a two digit positive number is 24. If 18 is added to
the number then the digits of the number are interchanged. Find the number.
Solution
Let
the digit at ten's place = x
Then,
digit at one's place = 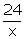
 Original number = 10x +
Original number = 10x + 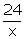 On
interchanging the digits, new number =
On
interchanging the digits, new number = 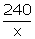 + x
According
to the question,
10x
+
+ x
According
to the question,
10x
+ 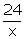 + 18 =
+ 18 = 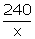 + x
10x2
+ 24 + 18x = 240 + x2
9x2
+ 18x - 216 = 0
x2
+ 2x - 24 = 0
(x
+ 6) (x - 4) = 0
x
= -6 or 4
But
x can't be negative, so, x = 4
+ x
10x2
+ 24 + 18x = 240 + x2
9x2
+ 18x - 216 = 0
x2
+ 2x - 24 = 0
(x
+ 6) (x - 4) = 0
x
= -6 or 4
But
x can't be negative, so, x = 4
 Digit at ten's place = x = 4 and digit at
one's place =
Digit at ten's place = x = 4 and digit at
one's place =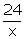 = 6
Thus,
the original number is 46.
= 6
Thus,
the original number is 46.
Q52. Which of the following in not a quadratic equation?
Solution
Simplify each option.
Consider,
x(x + 1) + 8 = (x + 2) (x - 2)
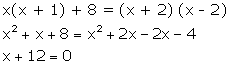 Clearly, this is a linear equation and not a quadratic equation.
Clearly, this is a linear equation and not a quadratic equation.
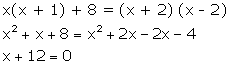 Clearly, this is a linear equation and not a quadratic equation.
Clearly, this is a linear equation and not a quadratic equation.
Q53. By
increasing the speed of a bus by 10 km/hr, it takes one and half hours less
to cover a journey of 450 km. Find the original speed of the bus.
Solution
Let
speed of the bus be x km/hr
Time
t = 450/x
If
speed is x + 10, then time T = 450/(x + 10)
By
question,
450/x
- 450/(x + 10) =3/2
450
(x + 10) -450 x = (3/2) (x2 + 10x)
4500
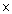 2 = 3 x2
+ 30x
x2
+ 10x - 3000 = 0
x
(x + 60) - 50x - 3000 = 0
x
(x + 60) - 50 (x + 60) = 0
x
= 50 (asx = -60 not possible )
2 = 3 x2
+ 30x
x2
+ 10x - 3000 = 0
x
(x + 60) - 50x - 3000 = 0
x
(x + 60) - 50 (x + 60) = 0
x
= 50 (asx = -60 not possible )
Q54. Solve
the quadratic equation by the completing the square method.
x2
+ 16x + 9 = 0
Solution
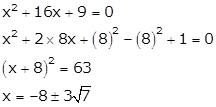
Q55. Solve
the below equation by the perfect square method:
x2 - 4x + 2 = 0
Solution
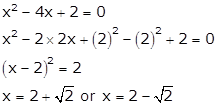
Q56. Solve
the quadratic equation by the formula method.
x2
+ x - 2 = 0
Solution
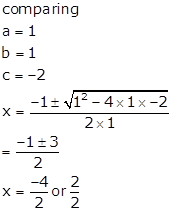 x
= −2 or x = 1
x
= −2 or x = 1
Q57. A person can buy 15 books less for Rs. 900 when the price of book goes up by Rs. 3. Find the original price and the no. of copies he would buy at initial price.
Solution
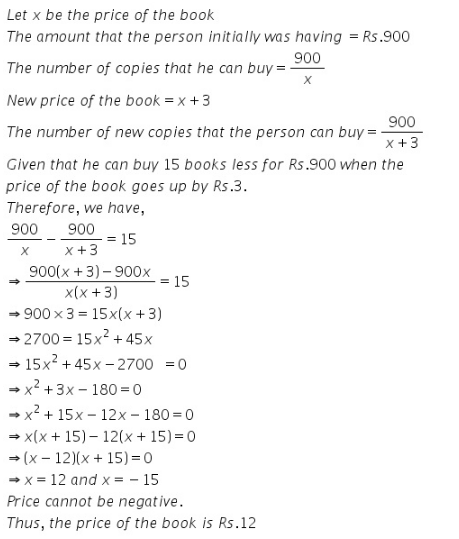 Therefore the number of copies that he can buy with the initial price
Therefore the number of copies that he can buy with the initial price 
Q58. Solve the following quadratic equations by factorization :


Solution

Q59. Two positive numbers differ by 3 and their product is 504. Find the numbers.
OR
Solve for x: 10ax2 - 6x + 15ax - 9 = 0 ; a 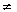 0
0
Solution
Let the numbers be x, x + 3.
x (x + 3) = 504
x2 + 3x - 504 = 0
(x + 24)(x - 21) = 0
x = 21, - 24
The numbers are positive so we reject x = -24.
Hence, the numbers are 21, 24.
OR
10ax2 - 6x + 15ax - 9 = 0
2x(5ax - 3) + 3(5ax - 3) = 0
(5ax-3) (2x + 3) = 0
5ax - 3 = 0 or 2x + 3 = 0
5ax = 3 or 2x = -3
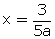 or
or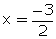
Q60. 

Solution

Q61. Solve
the below equation by the factorisation method:
x2
- 7x + 12 = 0
Solution
x2
- 7x + 12 = 0
x2 - 4x - 3x + 12 = 0
x(x - 4) - 3(x - 4) = 0
(x - 4)(x - 3) = 0
x = 4 or x = 3
Q62. If x2 + 2 kx + 4 = 0 has a root x = 2, then the value of k is?
Solution
It is given that x2 + 2 kx + 4 = 0 has a root x = 2.
 (2)2 + 2k(2) + 4 = 0
4 + 4k + 4 = 0
4k + 8 = 0
4k = -8
k = -2
(2)2 + 2k(2) + 4 = 0
4 + 4k + 4 = 0
4k + 8 = 0
4k = -8
k = -2
Q63. Solve
the quadratic equation by the formula method.
x2
+ 3x - 7 = 0
Solution
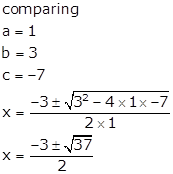
Q64. Solve the following quadratic equations by factorization :
4x2 + 5x = 0
Solution
Consider the given quadratic equation,
4x2 + 5x = 0
x (4x + 5) = 0
⇒x = 0 or 4x + 5 = 0
⇒x = 0 or 4x = -5


Q65. 

Solution
Let the first number be x then the second number be 15 - x.
According to the given condition,




Q66. A train travels at a uniform speed for a
distance of 63 km and then travels a distance of 72 km at an average speed of
6 km/h more than its original speed. If it takes 3 hours to complete the
total journey, what is the original speed of the train?
Solution
Let
original speed of the train be x km/h.
Then,
time taken to travel 63 km = 63/x hours
New
speed = (x + 6) km/hr
Time
taken to travel 72 km = 72/(x + 6) hours
According
to the question,
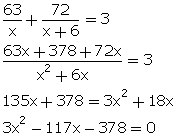 x2
- 39x - 126 = 0
(x
- 42)(x + 3) = 0
x
= -3 or x = 42
As
the speed cannot be negative, x = 42
Thus,
the average speed of the train is 42 km/hr.
x2
- 39x - 126 = 0
(x
- 42)(x + 3) = 0
x
= -3 or x = 42
As
the speed cannot be negative, x = 42
Thus,
the average speed of the train is 42 km/hr.
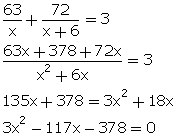 x2
- 39x - 126 = 0
(x
- 42)(x + 3) = 0
x
= -3 or x = 42
As
the speed cannot be negative, x = 42
Thus,
the average speed of the train is 42 km/hr.
x2
- 39x - 126 = 0
(x
- 42)(x + 3) = 0
x
= -3 or x = 42
As
the speed cannot be negative, x = 42
Thus,
the average speed of the train is 42 km/hr.
Q67. Sum of the area of two squares is 468 m2. If the difference of their perimeters is 24 m, find the sides of the two squares.
Solution
Let the side of the squares be x and y meters.
Areas of first square and second square are x2 and y2 respectively.
Perimeters of first and second squares are 4x and 4y respectively.
From the given information, we have:
x2 + y2 = 468… (1)
4x - 4y = 24
x - y = 6
y = x - 6
Substituting the value of y in (1), we get
x2 + (x - 6)2 = 468
x2 + x2 +36 - 12x = 468
2x2 - 12x - 432 = 0
x2 - 6x - 216 = 0
(x - 18)(x + 12) = 0
x = 18 or x = -12
As the side cannot be negative, x = 18
Hence, side of the first square is 18 m.
Side of the second square is y = (18 - 6) m = 12 m
Q68. A two
digit number is such that the product of the digits is 18. When 63 is
subtracted from the number, the digits interchange their places. Find the
number.
Solution
Let
unit's digit is x and ten's digit = 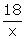
 Number =
Number = 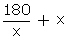 On
interchanging the digits the number becomes 10x +
On
interchanging the digits the number becomes 10x + 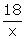
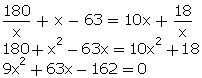 x2
+ 7x - 18 = 0
x2
- 2x + 9x - 18 = 0
x(x
- 2) + 9(x - 2) = 0
(x - 2) (x + 9) = 0
x2
+ 7x - 18 = 0
x2
- 2x + 9x - 18 = 0
x(x
- 2) + 9(x - 2) = 0
(x - 2) (x + 9) = 0
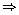 x = -9 or x = 2
Neglecting
the negative value, x = 2.
Therefore,
the number is 92.
x = -9 or x = 2
Neglecting
the negative value, x = 2.
Therefore,
the number is 92.
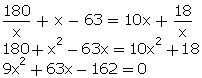 x2
+ 7x - 18 = 0
x2
- 2x + 9x - 18 = 0
x(x
- 2) + 9(x - 2) = 0
(x - 2) (x + 9) = 0
x2
+ 7x - 18 = 0
x2
- 2x + 9x - 18 = 0
x(x
- 2) + 9(x - 2) = 0
(x - 2) (x + 9) = 0
Q69. For what values of k, the roots of the quadratic equation (k + 4) x2 + (k + 1)x + 1 = 0 are equal?
Solution
(k + 4)x2 + (k + 1)x + 1 = 0
a = k + 4, b = k + 1, c = 1
For equal roots, D = 0
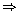 b2 - 4ac = 0
b2 - 4ac = 0
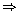 (k + 1)2 - 4(k + 4) ×1 = 0
(k + 1)2 - 4(k + 4) ×1 = 0
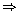 k2 + 2k + 1 - 4k - 16 = 0
k2 + 2k + 1 - 4k - 16 = 0
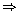 k2 - 2k - 15 = 0
k2 - 2k - 15 = 0
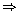 k2 - 5k + 3k - 15 = 0
k2 - 5k + 3k - 15 = 0
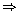 k(k - 5) + 3(k - 5) = 0
k(k - 5) + 3(k - 5) = 0
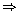 (k - 5) (k + 3) = 0
(k - 5) (k + 3) = 0
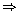 k = 5 or k = -3
Thus, for k = 5 or k = - 3, the given quadratic equation has equal roots.
k = 5 or k = -3
Thus, for k = 5 or k = - 3, the given quadratic equation has equal roots.
Q70. 

Solution
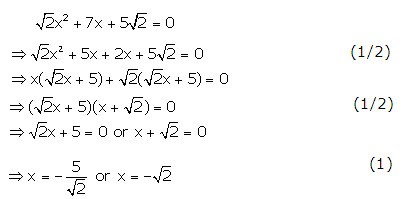
Q71. The difference of squares of two natural
numbers is 45. The square of the smaller number is four times the larger
number. Find the numbers.
Solution
Let
the two numbers be x and y such that y < x.
From
the given conditions, we have:
x2
- y2 = 45 … (1)
y2
= 4x … (2)
Using
(2) in (1), we have:
x2
- 4x - 45 = 0
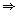 (x - 9)(x + 5) = 0
(x - 9)(x + 5) = 0
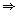 x = 9 (Rejecting the negative value of x)
From
(2), we get, y = 6 or -6
Rejecting
the negative value, we have, y = 6.
Thus,
the two numbers are 9 and 6.
x = 9 (Rejecting the negative value of x)
From
(2), we get, y = 6 or -6
Rejecting
the negative value, we have, y = 6.
Thus,
the two numbers are 9 and 6.
Q72. Find the roots of the following quadratic equation by the factorization method:
4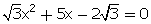
Solution
Q73. Some students arranged a picnic, the budget for food was Rs. 240. Because four students of the group failed to go, the cost of food to each student got increased by Rs. 5. How many students went for picnic?
Solution
Let number of student planned for picnic 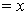 Budget for food = Rs. 240
Students left = 4
Hence, No. of students who went for picnic = x - 4
Earlier cost for each student =
Budget for food = Rs. 240
Students left = 4
Hence, No. of students who went for picnic = x - 4
Earlier cost for each student =  New cost for each student =
New cost for each student =  According to given information,
According to given information,
 Number of students went for the picnic = 16 - 4 = 12
Hence,12 students went for picnic.
Number of students went for the picnic = 16 - 4 = 12
Hence,12 students went for picnic.
 New cost for each student =
New cost for each student =  According to given information,
According to given information,
 Number of students went for the picnic = 16 - 4 = 12
Hence,12 students went for picnic.
Number of students went for the picnic = 16 - 4 = 12
Hence,12 students went for picnic.
Q74. Find
the roots of the quadratic equation 3x2 - 14x + 8 = 0.
Solution
3x2
- 14x + 8 = 0
3x2
- 12x - 2x + 8 = 0
3x(x
- 4) -2 (x - 4) = 0
(3x
- 2) (x - 4) = 0
x
= 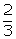 , x = 4
, x = 4
Q75. Solve for x:
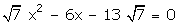
Solution
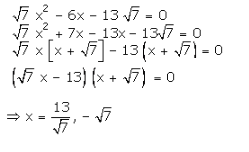
Q76. Find the values of k for which the following quadratic equation has two equal roots:
2x2 + kx + 3 = 0
Solution
Here, a = 2, b = k, c = 3
Since, the roots are equal,
D = 0
Or, k2 - 24 = 0




Q77. Find
the solution of the quadratic equation by the formula method.
x2
+ 9x - 3 = 0
Solution
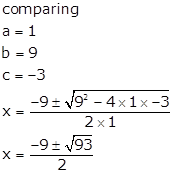
Q78. The angry Arjun carried some arrows for fighting with Bheeshm. With half the arrows, he cut down the arrows thrown by Bheeshm on him and with six other arrows he killed the charioter of Bheesham. With one arrow each he knocked down respectively the rath, flag and bow of Bheeshm. Finally with one more than four times the square root of arrows he laid Bheeshm unconscious on an arrow bed. Find total number of arrows Arjun had.
Solution

Q79. Two pipes can together fill a tank in 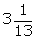 minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe can fill the tank.
minutes. If one pipe takes 3 minutes more than the other to fill it, find the time in which each pipe can fill the tank.
Solution
Let the faster pipe take x minutes to fill the tank.
Hence, the slower pipe takes x + 3 mins
In 1 min the faster pipe fill 1/x of the tank and the slower pipe fills 1/(x + 3) of the tank.
Part of the tank filled in 40/13 mins is (40/13) 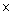 (1/(x+3))
Accoedingly,40/13x +40/13 (x + 3) = 1
40 [13(x + 3) + 13x] = 13 x
(1/(x+3))
Accoedingly,40/13x +40/13 (x + 3) = 1
40 [13(x + 3) + 13x] = 13 x 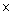 13 (x + 3)
13x2 - 41x - 120 = 0
13x2 - 65x + 24x - 120 = 0
13x (x - 5) + 24 (x - 5) = 0
(13x + 24) (x - 5) = 0
x = 5 [x = -13/24 is not possible].
Therefore, Faster pipe can fill in x = 5 minutes and Slower pipe in x + 3 = 5 + 3 = 8 mins
13 (x + 3)
13x2 - 41x - 120 = 0
13x2 - 65x + 24x - 120 = 0
13x (x - 5) + 24 (x - 5) = 0
(13x + 24) (x - 5) = 0
x = 5 [x = -13/24 is not possible].
Therefore, Faster pipe can fill in x = 5 minutes and Slower pipe in x + 3 = 5 + 3 = 8 mins
Q80. The sum of the squares of two positive integers is 208. If the square of the larger number is 18 times the smaller, find the numbers.
Solution
Let x and y be two positive integers.
Since the sum of the squares of two positive integers is 208, we have
x2 + y2 = 208…(1)
Also given that the square of the larger number is 18 times the smaller.
⇒ x2 = 18y…(2)
Substituting the value of x2 from equation (2) in equation (1), we get
18y + y2 = 208
⇒ y2 + 18y = 208
⇒ y2 + 18y - 208 = 0
⇒ y2 + 26y - 8y - 208 = 0
⇒ y(y + 26) - 8(y + 26)= 0
⇒ (y - 8) (y + 26) = 0
⇒ y - 8 = 0 or y + 26 = 0
⇒ y = 8 or y = -26
Since the numbers are positive integers, y = 8
And hence, x2 = 18y = 18 × 8 = 144
⇒ x = 12
Thus, the positive integers are 12 and 8.
Q81. Solve the following equation 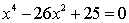
Solution
Put
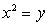 Then,
Then, 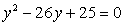
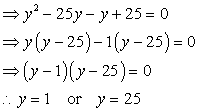
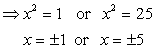
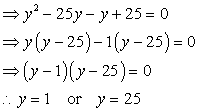
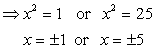
Q82. A plane left 30 min late due to bad
weather, but in order to reach its destination 1500 km away on time it has to
increase its speed by 250 km/hr. Find the original speed.
Solution
Let
the original speed of the plane be x.
Distance
= 1500 km
 Time
=
Time
= 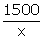 hrs
Given
that in order to reach its destination, the plane had to increase its speed
by 250 km/hr.
New
speed = (x + 250) km/hr
hrs
Given
that in order to reach its destination, the plane had to increase its speed
by 250 km/hr.
New
speed = (x + 250) km/hr
 New
Time =
New
Time = 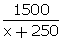 According
to question, we have:
According
to question, we have:
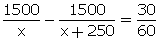
 x2
+ 250x - 750000 = 0
x2
+ 1000x - 750x - 750000 = 0
x(x
+ 1000) - 750(x + 1000) = 0
(x
+ 1000) (x - 750) = 0
x
= -1000 or 750
But
x, being the speed, cannot be negative. So, x = 750
Thus,
the original speed of the
plane was 750 km/hr.
x2
+ 250x - 750000 = 0
x2
+ 1000x - 750x - 750000 = 0
x(x
+ 1000) - 750(x + 1000) = 0
(x
+ 1000) (x - 750) = 0
x
= -1000 or 750
But
x, being the speed, cannot be negative. So, x = 750
Thus,
the original speed of the
plane was 750 km/hr.
Q83. Solve for x:
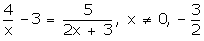
Solution
 8x + 12 - 6x2 - 9x = 5x
6x2 + 6x - 12 = 0
x2 + x - 2 = 0
(x + 2) (x - 1) = 0
x = -2, 1
8x + 12 - 6x2 - 9x = 5x
6x2 + 6x - 12 = 0
x2 + x - 2 = 0
(x + 2) (x - 1) = 0
x = -2, 1
Q84. Solve for x:
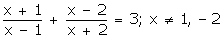
Solution

Q85. The quadratic equation whose roots are real and equal is:
Solution
Consider the equation x 2 - 4x + 4 = 0
x 2 - 4x + 4 = 0
(x-2)2=0
x=2
Thus, the roots of the equation x 2 - 4x + 4 = 0 are equal and real.
Q86. Solve for x:
9x2 - 3(a + b)x + ab = 0
Solution
9x2 - 3ax - 3bx + ab = 0
3x(3x - a) - b(3x - a) = 0
(3x-a)(3x-b)=0
3x-a=0 or 3x-b=0
x = 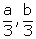
Q87. For what value(s) of p does the equation px2 + (p - 1)x + (p - 1) = 0 have a repeated root?
Solution

Q88. Solve
for x:
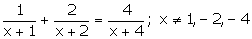
Solution
Q89. For what value of k the equation 4x2 - 2 (k + 1) x + (k + 1) = 0 has real and equal roots?
Solution
Comparing the given equation with the general form of a quadratic equation ax2 + bx + c = 0, we get
a = 4, b = -2 (k + 1), c = k + 1
D = 0, for real and equal roots
b2 - 4ac = 0
 4 (k + 1)2 - 16 (k + 1) = 0
4 (k + 1) (k + 1 - 4) = 0
(k + 1)(k - 3) = 0
k = -1, 3
Therefore, for k = -1, 3 the given quadratic equation has real and equal roots.
4 (k + 1)2 - 16 (k + 1) = 0
4 (k + 1) (k + 1 - 4) = 0
(k + 1)(k - 3) = 0
k = -1, 3
Therefore, for k = -1, 3 the given quadratic equation has real and equal roots.
Q90. Using quadratic formula solve the following quadratic equation 

Solution
Comparing the equation with
 we have
we have
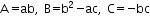 Now compute the discriminant.
Now compute the discriminant.
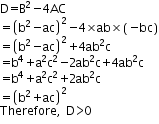 So the given equation has real roots
So the given equation has real roots
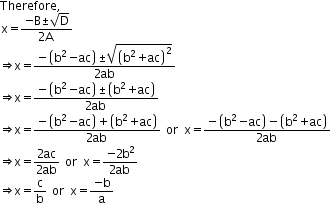
 we have
we have
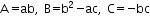 Now compute the discriminant.
Now compute the discriminant.
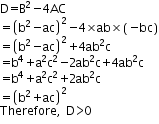 So the given equation has real roots
So the given equation has real roots
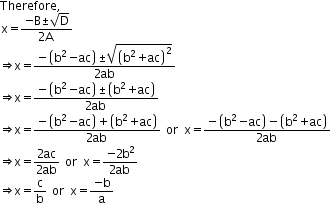
Q91. The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution
Let the base of the triangle  then altitude of the triangle
then altitude of the triangle  Hypotenuse = 13 cm
By Pythagoras theorem,
(Hypotenuse) 2 = (Base)2 + (altitude)2
Hypotenuse = 13 cm
By Pythagoras theorem,
(Hypotenuse) 2 = (Base)2 + (altitude)2
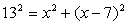
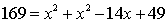

 Length can not be negative.
Hence, x = 12 cm
Altitude = x - 7 = 12 - 7 = 5 cm
Therefore the length of the other two sides are 12 cm and 5 cm.
Length can not be negative.
Hence, x = 12 cm
Altitude = x - 7 = 12 - 7 = 5 cm
Therefore the length of the other two sides are 12 cm and 5 cm.

 Length can not be negative.
Hence, x = 12 cm
Altitude = x - 7 = 12 - 7 = 5 cm
Therefore the length of the other two sides are 12 cm and 5 cm.
Length can not be negative.
Hence, x = 12 cm
Altitude = x - 7 = 12 - 7 = 5 cm
Therefore the length of the other two sides are 12 cm and 5 cm.
Q92. A takes 6 days less than the time taken by
B finish a piece of work. If both A and B together can finish it in 4 days,
find the time taken by B to finish the work.
Solution
Let the number of days taken by A to finish the work be x.
Then, number of days taken by B to finish the work = x + 6
Now, work done by A in one day = 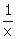 and work done
by B in one day =
and work done
by B in one day = 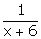 Now, we have:
Now, we have:
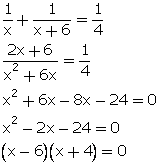 x = 6 (neglecting x = -4)
Thus, time taken by B to finish the work = x + 6 = 12 days
x = 6 (neglecting x = -4)
Thus, time taken by B to finish the work = x + 6 = 12 days
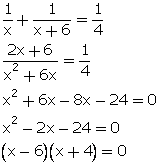 x = 6 (neglecting x = -4)
Thus, time taken by B to finish the work = x + 6 = 12 days
x = 6 (neglecting x = -4)
Thus, time taken by B to finish the work = x + 6 = 12 days
Q93. The length of a rectangular plot is greater than thrice its breadth by 2 m. The area of the plot is 120 sq. m. Find the length and breadth of the plot.
Solution
Let the breadth of the rectangular plot be x m, then length = (3x + 2) m
Area = 120
length × breadth = 120
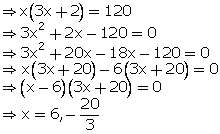 Rejecting the negative value, as breadth can't be negative.
Breadth of the rectangular plot = 6 m
Length of the rectangular plot = (3
Rejecting the negative value, as breadth can't be negative.
Breadth of the rectangular plot = 6 m
Length of the rectangular plot = (3  6 + 2) m = 20 m
6 + 2) m = 20 m
 Rejecting the negative value, as breadth can't be negative.
Breadth of the rectangular plot = 6 m
Length of the rectangular plot = (3
Rejecting the negative value, as breadth can't be negative.
Breadth of the rectangular plot = 6 m
Length of the rectangular plot = (3
Q94.
A factory produces certain pieces in a day. It was observed on a particular day that the cost of production of each piece (in rupees) was 3 more than twice the number of pieces produced in the day. If the total cost of production on that day was Rs. 90, find the number of pieces produced and cost of each piece.
Solution
Let the number of pieces per day = n
Cost of one pieces is C = 2n + 3
Total cost = Rs. 90 ... Given


Q95. Solve the given equation for x:
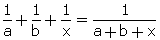
Solution

Q96. State whether the following equation is a quadratic equation or not:
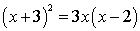
Solution
 Yes, it is a quadratic equation.
Yes, it is a quadratic equation.
Q97. Three consecutive positive integers are taken such that the sum of the square of the first and the product of the other two is 154. Find the integers.
Solution
Let the three consecutive positive integers be x, x + 1, x + 2.
x2 + (x + 1) (x + 2) = 154
x2 + (x2 + 3x + 2) = 154
2x2 + 3x - 152 = 0
2x2 - 16x + 19x - 152 = 0
2x (x - 8) + 19 (x - 8) = 0
(x - 8)(2x + 19) = 0
x = 8 or -19/2
But, x is a positive integer.
So, x = 8.
Thus, the numbers are 8, 9, 10.
Q98. The sum of the squares of two consecutive positive odd numbers is 130. Find the numbers.
Solution
Let the consecutive numbers be x, x + 2.
x2 + (x + 2)2 = 130
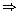 x2 + x2 + 4x + 4 = 130
x2 + x2 + 4x + 4 = 130
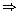 2x2 + 4x - 126 = 0
2x2 + 4x - 126 = 0
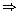 x2 + 2x - 63 = 0
x2 + 2x - 63 = 0
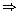 x2 + 9x - 7x - 63 = 0
x2 + 9x - 7x - 63 = 0
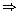 x(x + 9) - 7(x + 9) = 0
x(x + 9) - 7(x + 9) = 0
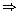 (x + 9) (x - 7) = 0
(x + 9) (x - 7) = 0
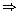 x = -9 or x = 7
Neglecting the negative value, we get, x = 7.
x = -9 or x = 7
Neglecting the negative value, we get, x = 7.
 The numbers are 7 and 9.
The numbers are 7 and 9.
Q99. Find the roots of quadratic equation  .
.
 .
.Solution
Let us split middle term 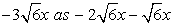
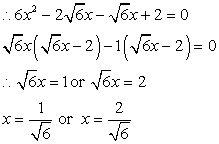 Therefore, the roots are
Therefore, the roots are  .
.
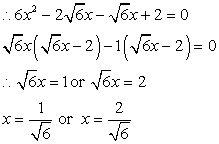 Therefore, the roots are
Therefore, the roots are  .
.
Q100. Solve for x:
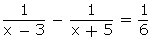
Solution

Q101. Solve the following equation for x.
9x2 - 9 (a + b) x + (2a2 + 5ab + 2b2) = 0
Solution
9x2 - 9(a + b) x + (2a2+ 5ba + 2b2) = 0
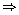 9x2 - 9(a + b)x + (2a + b) (a + 2b) = 0
9x2 - 9(a + b)x + (2a + b) (a + 2b) = 0
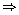 9x2 - 3(2a + b)x - 3 (a + 2b)x + (2a + b) (a + 2b) = 0
9x2 - 3(2a + b)x - 3 (a + 2b)x + (2a + b) (a + 2b) = 0
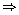 3x[3x - (2a + b)] - (a + 2b) [3x - (2a + b)] = 0
3x[3x - (2a + b)] - (a + 2b) [3x - (2a + b)] = 0
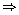 [3x - (2a + b)] [3x - (a + 2b)] = 0
[3x - (2a + b)] [3x - (a + 2b)] = 0
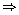 x =
x = 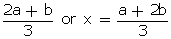
Q102. 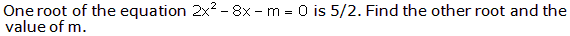
Solution
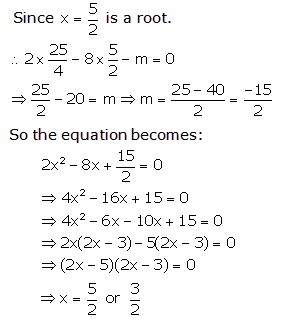
Q103. Sum of the areas of two squares is 468 m2. If the difference of their perimeters is 24m, find the sides of the two squares.
Solution
Sum of the areas of two squares = 468 m2
Let a and b be the sides of the two squares.
⇒a2 + b2 = 468…(1)
Also given that,
the difference of their perimeters = 24m
⇒4a - 4b = 24
⇒a - b = 6
⇒a = b + 6…(2)
We need to find the sides of the two squares.
Substituting the value of a from equation (2) in equation (1), we get
(b + 6)2 + b2 = 468
⇒b2 + 62 + 2 × b × 6 + b2 = 468
⇒2b2 + 36 + 12b = 468
⇒2b2 + 36 + 12b - 468 = 0
⇒2b2 + 12b - 432 = 0
⇒b2 + 6b - 216 = 0
⇒b2 + 18b - 12b - 216 = 0
⇒b(b + 18) - 12(b + 18) = 0
⇒(b + 18)(b - 12) = 0
⇒b + 18 = 0 or b - 12 = 0
⇒b = -18 = 0 or b = 12
Side cannot be negative and hence b = 12 m.
Therefore, a = b + 6 = 12 + 6 = 18 m.
Therefore the sides of the two squares are 12m and 18m.
Q104. A person has a rectangular garden whose area is 100 sq m. He fences three sides of the garden with 30 m barbed wire. On the fourth side, the wall of his house is constructed; find the dimensions of the garden.
Solution
Let the length and breadth of garden be x m and y m respectively.
Area of the garden = 100 sq m
xy = 100 sq m or y = 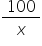 Suppose the person builds his house along the breadth of the garden.
Then, we have:
2x + y = 30
Suppose the person builds his house along the breadth of the garden.
Then, we have:
2x + y = 30
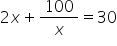 2x2 - 30x + 100 = 0
x2 - 15x + 50 = 0
x2 - 10x - 5x + 50 = 0
x(x - 10) - 5(x - 10) = 0
(x - 10) (x - 5) = 0
x = 10, x = 5
When x = 10 m, we have: y = 10 m
When x = 5 m, we have: y = 20 m
Thus, the dimensions of the garden are 10 m
2x2 - 30x + 100 = 0
x2 - 15x + 50 = 0
x2 - 10x - 5x + 50 = 0
x(x - 10) - 5(x - 10) = 0
(x - 10) (x - 5) = 0
x = 10, x = 5
When x = 10 m, we have: y = 10 m
When x = 5 m, we have: y = 20 m
Thus, the dimensions of the garden are 10 m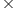 10 m or 5 m
10 m or 5 m 20 m.
20 m.
 Suppose the person builds his house along the breadth of the garden.
Then, we have:
2x + y = 30
Suppose the person builds his house along the breadth of the garden.
Then, we have:
2x + y = 30
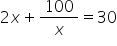 2x2 - 30x + 100 = 0
x2 - 15x + 50 = 0
x2 - 10x - 5x + 50 = 0
x(x - 10) - 5(x - 10) = 0
(x - 10) (x - 5) = 0
x = 10, x = 5
When x = 10 m, we have: y = 10 m
When x = 5 m, we have: y = 20 m
Thus, the dimensions of the garden are 10 m
2x2 - 30x + 100 = 0
x2 - 15x + 50 = 0
x2 - 10x - 5x + 50 = 0
x(x - 10) - 5(x - 10) = 0
(x - 10) (x - 5) = 0
x = 10, x = 5
When x = 10 m, we have: y = 10 m
When x = 5 m, we have: y = 20 m
Thus, the dimensions of the garden are 10 m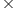 10 m or 5 m
10 m or 5 m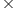 20 m.
20 m.
Q105. Find
value of p such that the quadratic equation
(p -
12)x2 - 2(p - 12)x + 2 = 0 has equal roots.
Solution
For
equal roots, D = 0, i.e., b2 - 4ac = 0
[-2(p
- 12)]2 - 4(p - 12) 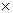 2 = 0
4(p
- 12)2 - 8(p - 12) = 0
4(p
- 12) (p - 12 - 2) = 0
(p
- 12) (p - 14) = 0
p
= 12 or p = 14
Rejecting
p = 12, as then the given equation will not be true. We have:
p
= 14
2 = 0
4(p
- 12)2 - 8(p - 12) = 0
4(p
- 12) (p - 12 - 2) = 0
(p
- 12) (p - 14) = 0
p
= 12 or p = 14
Rejecting
p = 12, as then the given equation will not be true. We have:
p
= 14
 = 0
= 0
Comments
Post a Comment