Q1. Solve the following pairs of Linear equation by substitution method
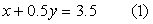
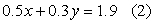
Solution
x + 0.5y = 3.5 ...(1)
0.5x + 0.3y = 1.9 ...(2)
From (1), x = 3.5 - 0.5y ....(3)
Putting this value in (2)
0.5(3.5 - 0.5y) + 0.3y = 1.9
1.75 - 0.25y + 0.3 y = 1.9
0.05y = 0.15
y = 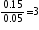 now putting y = 3 in (3)
x = 3.5 - (0.5 X 3) = 2
Hence x = 2 and y = 3 is the required solution
now putting y = 3 in (3)
x = 3.5 - (0.5 X 3) = 2
Hence x = 2 and y = 3 is the required solution
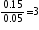 now putting y = 3 in (3)
x = 3.5 - (0.5 X 3) = 2
Hence x = 2 and y = 3 is the required solution
now putting y = 3 in (3)
x = 3.5 - (0.5 X 3) = 2
Hence x = 2 and y = 3 is the required solution
Q2. Prema invests a certain sum at the rate of 10% per annum
of interest and another sum at the rate of 8% per annum get an yield of Rs
1640 in one year's time. Next year she interchanges the rates and gets a
yield of Rs 40 less than the previous year. How much did she invest in each
type in the first year?
Solution
Let us assume that Prema
invests Rs x @10% and Rs y @8% in the first year.
We know that
Interest =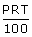 ATQ,
ATQ,
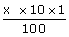 +
+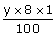 =1640
Þ 10x+8y=164000………..(i)
Next,
After interchanging,
=1640
Þ 10x+8y=164000………..(i)
Next,
After interchanging,
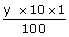 +
+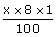 =1600
we get 10y+8x=160000..
8x+10y=160000...(ii)
Adding (i) and
(ii)
18x+18y=324000
18x+18y=324000
Þ x + y = 18000 ..(iii)
Subtracting (ii) from (i)
2x-2y=4000
Þ x - y = 2000...(4)
Adding (3) and (4)
2x=20000
Þ x = 10000
Substituting this value of x
in (3)
y=8000
So the sums invested in the
first year at the rate 10% and 8% are Rs 10000 and Rs 8000 respectively.
=1600
we get 10y+8x=160000..
8x+10y=160000...(ii)
Adding (i) and
(ii)
18x+18y=324000
18x+18y=324000
Þ x + y = 18000 ..(iii)
Subtracting (ii) from (i)
2x-2y=4000
Þ x - y = 2000...(4)
Adding (3) and (4)
2x=20000
Þ x = 10000
Substituting this value of x
in (3)
y=8000
So the sums invested in the
first year at the rate 10% and 8% are Rs 10000 and Rs 8000 respectively.
Q3. For which values of p does the pair of equations given below have unique solution.
4x + py + 8 = 0; 2x + 2y + 2 = 0
Solution
The given pair of linear equations are:
4x + py + 8 = 0 ........ (i) and
2x + 2y + 2 = 0 ........ (ii)
We know that the pair of linear equations a1 x + b1 y +c1 = 0 and a2 x + b2 y + c2 = 0 has unique solution if
 Substituting values of a1, b1, a2, b2, we get,
Substituting values of a1, b1, a2, b2, we get,
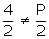
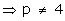 Thus, for all values of p except 4, the given pair of equations will have a unique solution.
Thus, for all values of p except 4, the given pair of equations will have a unique solution.
 Substituting values of a1, b1, a2, b2, we get,
Substituting values of a1, b1, a2, b2, we get,
Q4. Seema has decided a fixed distance to walk on a
tread mill. First day she walks at a certain speed. Next day, she increases the
speed of the tread mill by 1 kmph, she takes 6 minutes less and if she
reduces the speed by 1 kmph, then she takes 9 minutes more. What is the
distance that she has decided to walk every day?
Solution
Let Seema walk at x kmph first day.
Let the time taken on first day be y hrs.
When she increases her speed by 1 kmph,
(x+1)(y-0.1)=xy …….(i)
When she decreases her speed by 1 kmph,
(x-1)(y+0.15)=xy ……….(ii)
Solving
(i), we get
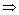 -0.1x + y=0.1 ---(iii)
Solving
(ii), we get
0.15x - y = 0.15 ---(iv)
Adding the equations (iii) and (iv) we get,
0.05 x=0.25
-0.1x + y=0.1 ---(iii)
Solving
(ii), we get
0.15x - y = 0.15 ---(iv)
Adding the equations (iii) and (iv) we get,
0.05 x=0.25
 x=5
Substituting this value of x in (iii) we get,
y = 0.1 + 0.5 = 0.6
The distance that Seema decided to walk
everyday =xy=5
x=5
Substituting this value of x in (iii) we get,
y = 0.1 + 0.5 = 0.6
The distance that Seema decided to walk
everyday =xy=5  0.6= 3 km
0.6= 3 km
Q5. Q.1.two places a & b are 120 km apart from each other on a highway. One car starts from a and other from b,at the same time. If they move in a same direction they meet in 6 hrs and if they move in opposite direction they meet in 1 hr and 12 mins.Find their speeds.
Q.2.A taxi charges in a city comprise of a fixed charge together with the charge for the distance covered. For a journey of 10 km the charge paid is Rs 75 and for the journey of 15 km.The charge paid is Rs.110. What will a person have to pay for travelling a distance of 25 km?
Solution

Q6. Using method of substitution solve the following system of linear equations.
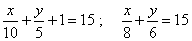
Solution
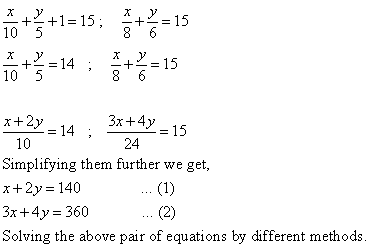
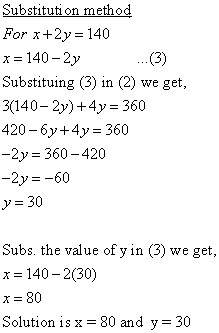
Q7. Solve the following:


Solution

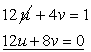
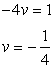 Putting this value of v in (3) we get
Putting this value of v in (3) we get


 or x=6
or x=6
 or
or
Q8. The pair of equations y = 0 and y = -7 has :
Solution
Since the x-axis (line y=0) does not intersect the line y=-7 at any point.
So, the pair of equations has no solution.
Q9. Solve
: 99x + 101y = 499
101x + 99y = 501
Solution
99x
+ 101y = 499 … (1)
101x
+ 99y = 501 … (2)
Adding
equations (1) and (2), we get.
200x + 200y = 1000
Or, x + y = 5 …
(3)
Subtracting (1) from (2), we get,
2x - 2y = 2
Or, x - y = 1 …
(4)
Adding (3) and (4), we get,
2x = 6  x = 3
Putting
the value of x in (3), we get,
y
= 2
x = 3
Putting
the value of x in (3), we get,
y
= 2
Q10. For what value of p, will the following system of linear equations have no solution?
(2p - 1)x + (p - 1) y = 2p + 1; y + 3x - 1 = 0
Solution
The given pair of linear equations are:
(2p - 1)x + (p - 1) y - (2p + 1) = 0 ........ (i) and
y + 3x - 1 = 0 ......... (ii)
We know that the pair of linear equations a1 x + b1 y +c1 = 0 and a2 x + b2 y + c2 = 0 has no solution if




Q11. Draw the graphs of the following equations: x + y = 5, x - y = 5.
(i) Find the solution of the equations from the graph.
(ii) Shade the triangular region formed by the lines and the y - axis.
Solution
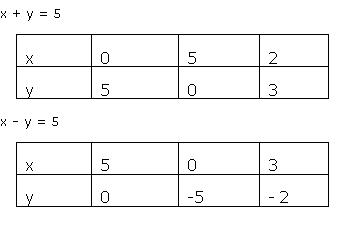 Plotting the points obtained by first equation and joining them.
Similarly, plotting the points obtained by second equation and plotting them on the same graph paper, we have:
Plotting the points obtained by first equation and joining them.
Similarly, plotting the points obtained by second equation and plotting them on the same graph paper, we have:
 The solution of the pair of equations will be the point where the two lines meet each other.
Hence, x = 5, y = 0 is the required solution.
The co-ordinates of the vertices of the triangle formed by these two lines and the y-axis are (0, 5), (0, -5) and (5, 0).
The solution of the pair of equations will be the point where the two lines meet each other.
Hence, x = 5, y = 0 is the required solution.
The co-ordinates of the vertices of the triangle formed by these two lines and the y-axis are (0, 5), (0, -5) and (5, 0).
Q12. 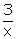 - 5y + 1 = 0,
- 5y + 1 = 0, 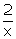 - y + 3 = 0
- y + 3 = 0
Solution
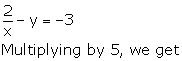

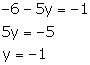
Q13. Solve for x and y:
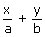 = 2; ax - by = a2 - b2
= 2; ax - by = a2 - b2
Solution

Q14. Which of the following is not a solution of the pair of equations 3x - 2y = 4 and 6x - 4y = 8?
Solution
The system of equations are 3x - 2y = 4 and 6x - 4y = 8.
Since,  , the system of equations has infinitely many solutions.
Putting x = 2 in one of the equations, we get y = 1.
Putting x = 4 in one of the equations, we get y = 4.
Putting x = 6 in one of the equations, we get y = 7.
Putting x = 5 in one of the equations, we get y = 5.5.
Thus, x = 5 and y = 3 is not a solution of the given pair of equations.
, the system of equations has infinitely many solutions.
Putting x = 2 in one of the equations, we get y = 1.
Putting x = 4 in one of the equations, we get y = 4.
Putting x = 6 in one of the equations, we get y = 7.
Putting x = 5 in one of the equations, we get y = 5.5.
Thus, x = 5 and y = 3 is not a solution of the given pair of equations.
Q15. Solve for x and y
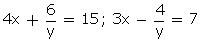
Solution
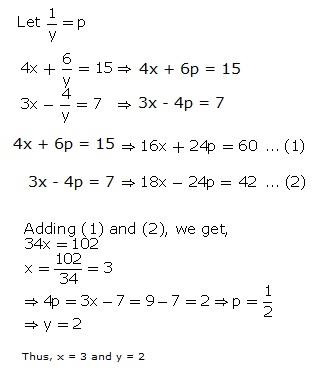
Q16. Solve :
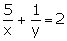
 ;
x
;
x 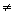 0,y
0,y  0
0
Solution
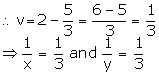 Hence, x = 3 and y = 3.
Hence, x = 3 and y = 3.
Q17. Solve the following system of linear equations graphically:x - y = 1, 2x + y = 8
Solution

Q18. A man travels 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and car.
Solution


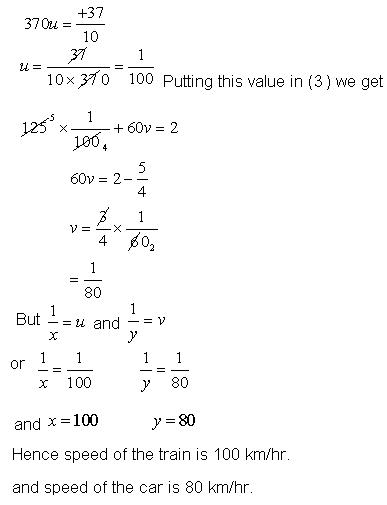
Q19. Place
A and B are 100 km apart on a highway. One car starts from A and another from
B at the same time. If the cars travel in the same direction at different
speeds, they meet in 5 hours. If they travel towards each other they meet in
1 hour. What are the speeds of the two cars?
Solution
Let
the speed of car at A be x kmph
and
the speed of car at B be y kmph
As
per the question,
5x - 5y = 100
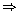 x - y =
20 ... (1)
and x + y = 100 ... (2)
Solving
(1) and (2), we get,
x
= 60 and y = 40
x - y =
20 ... (1)
and x + y = 100 ... (2)
Solving
(1) and (2), we get,
x
= 60 and y = 40
 Speed of the car at A = 60 kmph
Speed
of the car at B = 40 kmph
Speed of the car at A = 60 kmph
Speed
of the car at B = 40 kmph
Q20. A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can go 40 km upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Solution
Let speed of boat in still water be x km/h and speed of stream be y km/h.
Speed upstream= (x - y) km/h
Speed downstream= (x + y) km/h
 On subtracting, we get,
On subtracting, we get,
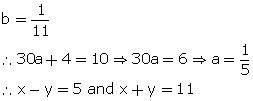 On solving, we get,
On solving, we get,
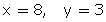
 Speed of boat in still water = 8 km/h
And, Speed of stream = 3 km/h
Speed of boat in still water = 8 km/h
And, Speed of stream = 3 km/h
 On subtracting, we get,
On subtracting, we get,
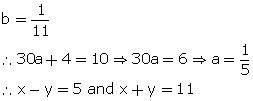 On solving, we get,
On solving, we get,
Q21. In the figure below, ABCDE is a pentagon with BE||CD and BC||DE.
BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm, find the value
of x and y.
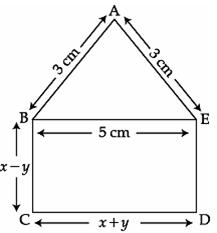

Solution
Since
BC || DE and BE || CD with BC 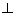 CD, BCDE is a
rectangle.
CD, BCDE is a
rectangle.
 Its opposite sides are equal.
i.e.,
BE = CD
Its opposite sides are equal.
i.e.,
BE = CD
 x + y = 5 ... (1)
and
DE = BC = x - y
Given,
perimeter of ABCDE is 21 cm.
AB
+ BC + CD + DE + EA = 21
3
+ x -
x + y = 5 ... (1)
and
DE = BC = x - y
Given,
perimeter of ABCDE is 21 cm.
AB
+ BC + CD + DE + EA = 21
3
+ x - 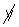 + x +
+ x + 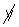 + x - y + 3 =
21
6
+ 3x - y = 21
3x
- y = 15 ... (2)
Adding
(1) and (2) : 4x = 20
+ x - y + 3 =
21
6
+ 3x - y = 21
3x
- y = 15 ... (2)
Adding
(1) and (2) : 4x = 20 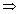 x = 5
x = 5
 y
= 5 - 5 = 0 [Using (1)]
y
= 5 - 5 = 0 [Using (1)]
Q22. Which of the following pairs of equations represent inconsistent system?
Solution
For the system of equations:
3x - y = -8
3x - y = 24
We have:
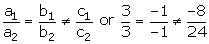 Therefore, the equations are inconsistent.
Therefore, the equations are inconsistent.
Q23. 

Solution

Q24. The pair of linear equations 8x - 5y = 7 and 5x - 8y = -7 have :
Solution
Q25. Solve
for x and y:-
37x +
41y = 70
41x +
37y = 86
Solution
37x
+ 41y = 70 ...(1)
41x
+ 37y = 86 ...(2)
Adding
(1) and (2), we get,
78x
+ 78y = 156
x
+ y = 2 ...(3)
Subtracting
(2) from (1), we get,
-4x
+ 4y = -16
y
- x = -4 ...(4)
(3)
+ (4) gives 2y = -2 or y = -1
 x = 3
Hence,
x = 3 and y = -1
x = 3
Hence,
x = 3 and y = -1
Q26. For what values of a and b, does the following pair of linear equations have an infinite number of solutions ?
2x +3y = 7; a(x + y) - b(x - y) = 3a + b - 2.
Solution
The given equations are:
2x + 3y = 7
or, 2x + 3y - 7 = 0
a(x + y) - b(x - y) = 3a + b - 2
or, x(a - b) + y (a + b) - (3a + b - 2) = 0
For infinite solutions, we have:
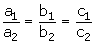
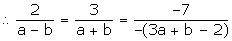
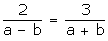 a = 5b ... (1)
a = 5b ... (1)
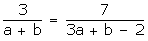 -a + 2b = -3 ... (2)
Solving (1) and (2), we get,
a = 5;b = 1
-a + 2b = -3 ... (2)
Solving (1) and (2), we get,
a = 5;b = 1
Q27. Solving
the following system of linear equation by substitution method:
2x
- y = 2
x
+ 3y = 15
Solution
2x
- y = 2
y
= 2x - 2 ...(1)
x
+ 3y = 15 ...(2)
Substituting
the value of y from (1) in (2), we get,
x
+ 6x - 6 = 15
7x
= 21
x
= 3
From
(1),
y
= 2 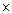 3 - 2 = 4
3 - 2 = 4
Q28. Solve the system of equations17x+53y= 10653x+17y= 34
Solution
The given system is17x+53y= 106...(1)53x+17y=34..(2)Adding the two equationsWe get,70x+70y=140 x+y=2...(3)Subtracting (2) from (1) we get,-36x+36y=72 x -y=-2..(4)Now,Adding (3) and (4)2x=0 x=0Substitutting this value of x in (3)We get,y=2So the solution to the system isx=0, y=2
Q29. Solve graphically: 2x - y = 2 and 4x - y = 4, shade the region between these lines and the y-axis.
Solution
2x - y = 2… (1)
4x - y = 4… (2)
For line (1),
x
0
1
2
y
-2
0
2
For line (2),
x
1
0
2
y
0
-4
4
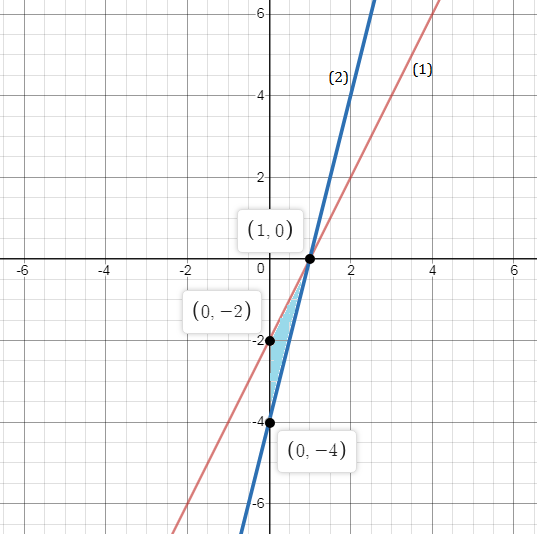 The two lines intersect at a point (1, 0).
Hence, the solution of these two lines is x=1, y=0.
The shaded region between the given lines and the y-axis is shown in the graph.
The two lines intersect at a point (1, 0).
Hence, the solution of these two lines is x=1, y=0.
The shaded region between the given lines and the y-axis is shown in the graph.
 The two lines intersect at a point (1, 0).
Hence, the solution of these two lines is x=1, y=0.
The shaded region between the given lines and the y-axis is shown in the graph.
The two lines intersect at a point (1, 0).
Hence, the solution of these two lines is x=1, y=0.
The shaded region between the given lines and the y-axis is shown in the graph.
Q30. Solve for x and y :  + 5y = 7;
+ 5y = 7;
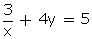
 + 5y = 7;
+ 5y = 7;
Solution
Let  = a
So, the given equations become:
= a
So, the given equations become:

 y = -1
Putting y = -1 in (1),
4a+ 5 (-1) = 7
4a = 12
a = 3
y = -1
Putting y = -1 in (1),
4a+ 5 (-1) = 7
4a = 12
a = 3

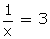
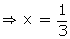
 = a
So, the given equations become:
= a
So, the given equations become:

Q31. A taken 3 hours more than B to walk 30 km. But if A doubles his pace, he is ahead of B by 
 hours. Find their speed of walking.
hours. Find their speed of walking.

 hours. Find their speed of walking.
hours. Find their speed of walking.Solution
Let speed of 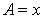 km/hr.
and
km/hr.
and 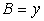 km/hr.
Therefore according to the question we get two equation.
km/hr.
Therefore according to the question we get two equation.
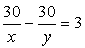 ……..(1)
……..(1)
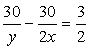 ……..(2)
Now Let
……..(2)
Now Let  Then equation (1) and (2) becomes
Then equation (1) and (2) becomes
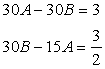 or
or 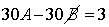 …….. (3)
…….. (3)
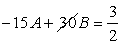 …….. (4)
Adding (3) and (4) we get
…….. (4)
Adding (3) and (4) we get
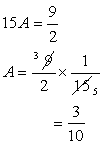 Putting this value of A in (3) we get
Putting this value of A in (3) we get
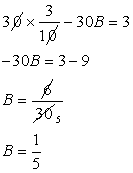 But
But  and
and  Hence speed of A is
Hence speed of A is  km/hr and B is 5 km/hr.
km/hr and B is 5 km/hr.
 Then equation (1) and (2) becomes
Then equation (1) and (2) becomes
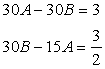 or
or 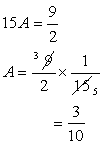 Putting this value of A in (3) we get
Putting this value of A in (3) we get
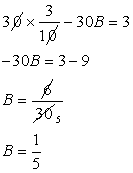 But
But  and
and  Hence speed of A is
Hence speed of A is  km/hr and B is 5 km/hr.
km/hr and B is 5 km/hr.
Q32. The
students of a class are made to stand in rows. If three students are extra in
each row, there would be 1 row less. If 3 students are less in a row, there
would be 2 rows more. Find the number of students in the class.
Solution
Let
the number of rows be x
Number
of students in 1 row = y
According
to the question,
(y + 3) (x - 1) = xy  xy + 3x - y -
3 = xy
Or 3x - y = 3 ...(1)
(y - 3) (x + 2) = xy
xy + 3x - y -
3 = xy
Or 3x - y = 3 ...(1)
(y - 3) (x + 2) = xy  xy - 3x + 2y -
6 = xy
Or
-3x + 2y = 6 ...(2)
Adding
(1) and (2), we get,
y = 9
xy - 3x + 2y -
6 = xy
Or
-3x + 2y = 6 ...(2)
Adding
(1) and (2), we get,
y = 9
 3x - 9 = 3
3x - 9 = 3 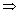 x = 4
x = 4
 Number of students = xy = 4
Number of students = xy = 4  9 = 36
9 = 36
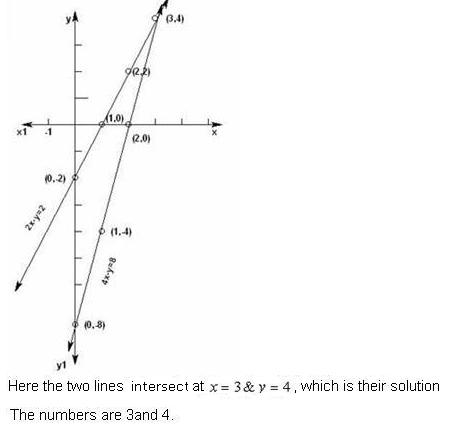
Q33. If we subtract a number from twice of other number we get 2, but if we subtract the same number from 4 time the other we get 8. Make the linear equation for the situation and solve it graphically.
Solution

Q34. The sum of 2 numbers is 51. If larger is doubled and smaller is tripled, the difference is 12. Find the numbers.
Solution
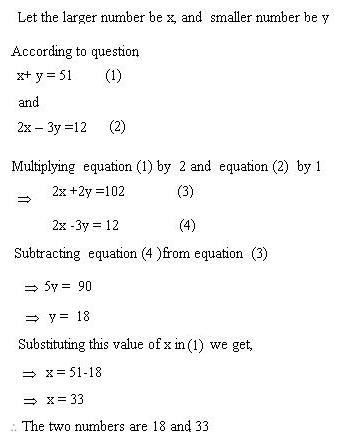
Q35. Form a pair of linear equations for the following problem, and find the solution graphically.
"10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz."
Solution
Let the number of girls and boys in the class be x and y respectively.
According to the given conditions, we have:
x + y = 10 ..... (i)
x - y = 4 ..... (ii)
x + y = 10  x = 10 - y
Three solutions of this equation can be written in a table as follows:
x
5
4
6
7
y
5
6
4
3
x - y = 4
x = 10 - y
Three solutions of this equation can be written in a table as follows:
x
5
4
6
7
y
5
6
4
3
x - y = 4 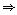 x = 4 + y
Three solutions of this equation can be written in a table as follows:
x
7
6
5
4
3
y
3
2
1
0
-1
The graphs of the two equations can be drawn as follows:
x = 4 + y
Three solutions of this equation can be written in a table as follows:
x
7
6
5
4
3
y
3
2
1
0
-1
The graphs of the two equations can be drawn as follows:
 From the graph, it can be observed that the two lines intersect each other at the point (7, 3).
So, x = 7 and y = 3 is the required solution of the given pair of equations.
Hence, the number of boys is 3 and number of girls is 7.
From the graph, it can be observed that the two lines intersect each other at the point (7, 3).
So, x = 7 and y = 3 is the required solution of the given pair of equations.
Hence, the number of boys is 3 and number of girls is 7.
 From the graph, it can be observed that the two lines intersect each other at the point (7, 3).
So, x = 7 and y = 3 is the required solution of the given pair of equations.
Hence, the number of boys is 3 and number of girls is 7.
From the graph, it can be observed that the two lines intersect each other at the point (7, 3).
So, x = 7 and y = 3 is the required solution of the given pair of equations.
Hence, the number of boys is 3 and number of girls is 7.
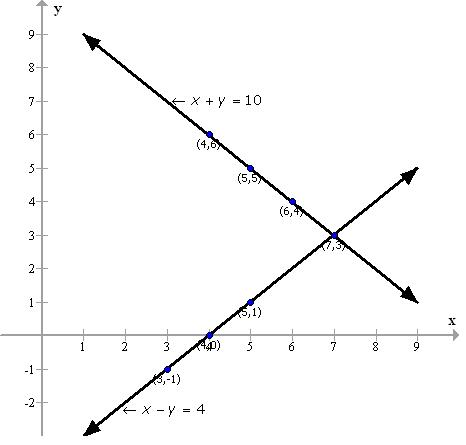
Q36. Solve x - y = 1 and 2x + y = 8 graphically and find the area of the region bounded by these lines and the x-axis.
Solution
(i) x - y = 1
y = x - 1
x
0
1
2
3
y
-1
0
1
2
(ii) 2x + y = 8
y = 8 - 2x
x
0
1
2
3
4
y
8
6
4
2
0
 The two lines intersect at point (3, 2). So, the solution of the given pair of linear equations is x = 3, y = 2.
Area of the required region (triangle)=
The two lines intersect at point (3, 2). So, the solution of the given pair of linear equations is x = 3, y = 2.
Area of the required region (triangle)=
 The two lines intersect at point (3, 2). So, the solution of the given pair of linear equations is x = 3, y = 2.
Area of the required region (triangle)=
The two lines intersect at point (3, 2). So, the solution of the given pair of linear equations is x = 3, y = 2.
Area of the required region (triangle)=
Q37. If x = a, y = b is the solution of the equations x - y = 2 and x + y = 4, then the values of a and b are, respectively.
Solution

Q38. One equation of a pair of dependent linear equations is -5x + 7y = 2, the second equation can be :
Solution
We know:
Dependent linear equations are the equations which represents the same line.
The given line is
-5x + 7y = 2
If we multiply by -2 throughout, we get
10x - 14y = -4
Thus, the required second equation is 10x - 14y = -4.
Q39. The sum of digits of a two digit number is 11. The number obtained by interchanging the digits of the given number exceeds the number by 63. Find the number.
Solution

Q40. The number of solutions of the pair of linear equations x + 2y - 8 = 0 and 2x + 4y = 16 are:
Solution
Comparing the given pair of linear equations with the general equations, we have,
a1 = 1, b1 = 2, c1 = -8
a2 = 2, b2 = 4, c2 = -16
It can be observed that:
 Thus, the given pair of linear equations has infinitely many solutions.
Thus, the given pair of linear equations has infinitely many solutions.
 Thus, the given pair of linear equations has infinitely many solutions.
Thus, the given pair of linear equations has infinitely many solutions.
Q41. 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Form the linear equation in two variables and then solve them graphically.
Solution
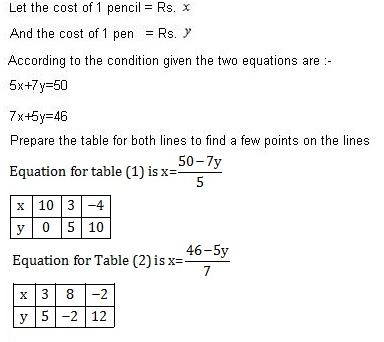

Q42. For what value of k will the following pair of linear equations have infinitely many solutions?kx + 3y - (k-3) = 012x + ky - k = 0
Solution

Q43. Draw the graph for the following equations:
y - x = 1
x + y = 3
Find the value of x and y using this graph. Also, shade the region bounded by these two lines and the line y = 0.
Solution
The given linear equations can be represented on a graph as below:
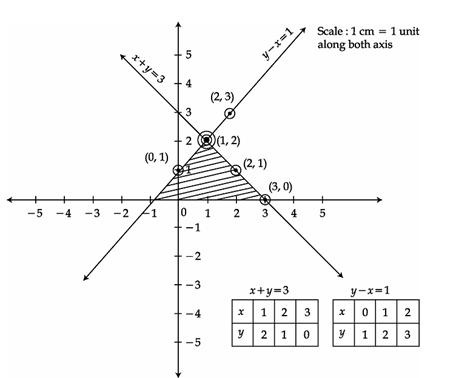 The point of intersection of these two lines will be the solution of the pair of equations.
The point of intersection of these two lines will be the solution of the pair of equations.
 Solution is given by:
x = 1, y = 2
Solution is given by:
x = 1, y = 2
 The point of intersection of these two lines will be the solution of the pair of equations.
The point of intersection of these two lines will be the solution of the pair of equations.
Q44. Solve for x and y:
7x+ 5y=74
7x+1-5y+1=218
Solution
7x+
5y=74
7x+1-5y+1=218
Let
7x =A, 5y =B
So the equations become
A + B=74 ...(i)
7A - 5B=218 ...(ii)
A=74-B, from (i)
Substituting it in (ii), we get:
7(74-B) - 5B=218
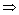 -12B=-300
-12B=-300
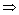 B=25
Substituting this value of B in equation (i) we
get,
A=49
B=25
Substituting this value of B in equation (i) we
get,
A=49
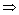 7x=49
and 5y=25
7x=49
and 5y=25
 x=2 and
y=2
So the solution to the given system of
equations is x=2, y=2.
x=2 and
y=2
So the solution to the given system of
equations is x=2, y=2.
Q45. If 2 pieces of spring rolls and 3 pieces of momos cost 35 rupees and 4 pieces of spring rolls and 6 pieces of momos cost 70 rupees. What may be the price of the two items?
Solution

Q46. Solve the following pairs of Linear equation by substitution method.
Solution
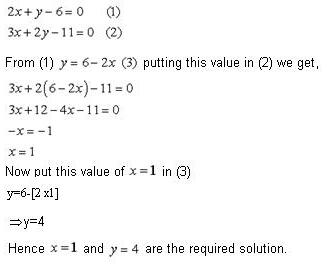
Q47. Seven times a two
digit number is equal to four times the number obtained by reversing the
order of its digits. If the difference between the digit is 3, find the
number.
Solution
Let the tens and units digit of the number be x
and y respectively.
7(10x + y) = 4(10y + x)  66x
66x  33y
33y  y = 2x
y - x = 3
On solving the two equations, we get,
x = 3, y = 6
Therefore, the number is 36.
y = 2x
y - x = 3
On solving the two equations, we get,
x = 3, y = 6
Therefore, the number is 36.
Q48. Solve graphically the pair of equations 2x + 3y = 11 and 2x - 4y = -24. Hence, find the coordinate of the vertices of the triangle so formed.
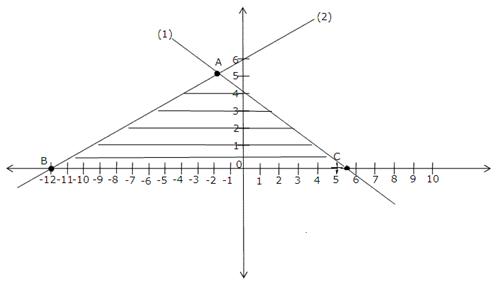
Solution
2x + 3y = 11 … (1)
2x - 4y = -24 … (2)
For line (1):
x
1
4
-2
y
3
1
5
For line (2):
x
-12
0
-10
y
0
6
1
From the graph, the point of intersection of the given lines is x = -2, y = 5.
The triangle formed is shaded as  ABC. The coordinates of the vertices of the triangle are A (-2, 5), B (-12, 0) and C (5.5, 0).
ABC. The coordinates of the vertices of the triangle are A (-2, 5), B (-12, 0) and C (5.5, 0).

Q49. Two numbers are in the ratio 5:6. If 8 is subtracted from each of the numbers, the ratio becomes 4:5. Find the numbers
Solution
Let the two numbers be 5x and 6x.
From the given information, we have:
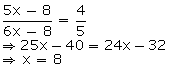 Thus, the two numbers are 40 and 48.
Thus, the two numbers are 40 and 48.
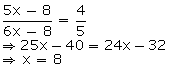 Thus, the two numbers are 40 and 48.
Thus, the two numbers are 40 and 48.
Q50. Solve the following pairs of Linear equation by substitution method
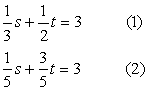
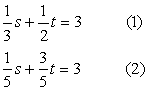
Solution

Q51. Solve for x and y:
148x + 231y = 527
231x + 148y = 610
Solution
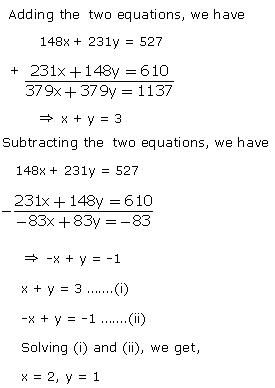
Q52. Solve:
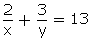
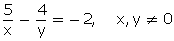
Solution
Q53. The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs 105 and for a journey of 15 km, the charge paid Rs. 155. What are the fixed charges and the charge per km?
Solution
Let the fixed charge of taxi be Rs x/km and the running charges be Rs y/km.
Then, according to given condition,
x + 10y = 105 ....(1)
x + 15y = 155 ....(2)
Subtracting, we get -5y = -50
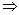 y = 10
Putting value of y in (1), we get
x = 105 - 10y
y = 10
Putting value of y in (1), we get
x = 105 - 10y 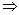 105 - 10(10) = 5
Therefore, fixed change of taxi is Rs 5/km and running charges is Rs 10/km.
105 - 10(10) = 5
Therefore, fixed change of taxi is Rs 5/km and running charges is Rs 10/km.
Q54. X takes 3 hours more than Y to walk 30 km. But if X doubles his pace, he is ahead of Y by 1 hours. Find their speeds of walking.
hours. Find their speeds of walking.
 hours. Find their speeds of walking.
hours. Find their speeds of walking.Solution
Let speed of X be p km/h
and speed of Y be q km/h
Time taken by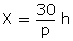 Time taken by
Time taken by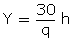
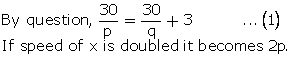 Then
Then 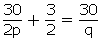 … (2)
Let
… (2)
Let 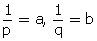 The two equations become:
30a = 30b + 3
The two equations become:
30a = 30b + 3
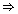 10a - 10b = 1
10a - 10b = 1
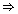 a - b =
a - b = 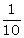 … (3)
And, 15a +
… (3)
And, 15a +  = 30b
15a - 30b =
= 30b
15a - 30b = 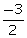 5a - 10b =
5a - 10b = 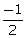 a - 2b =
a - 2b =  … (4)
(3) - (4) gives
b =
… (4)
(3) - (4) gives
b = 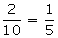
 From (3), we get,
a =
From (3), we get,
a = 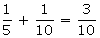
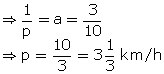
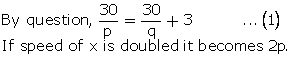 Then
Then 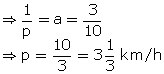
Q55. Using method of Elimination solve the following system of linear equations.
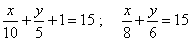
Solution
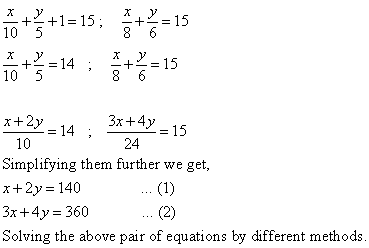
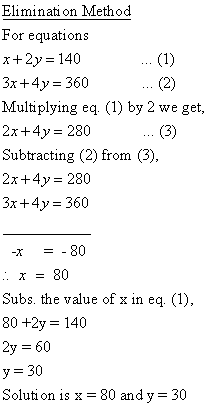
Q56. 10 years ago, father‘s age was 12 times that of his son and 10 years hence, his age would be twice that of his son. Find their present ages.
Solution

Q57. Two kids are discussing their ages. One says to other that 2 times my age added to your age gives 18 years. Also 3 times my age added to 2 times yours gives 29 years. what's their age
Solution
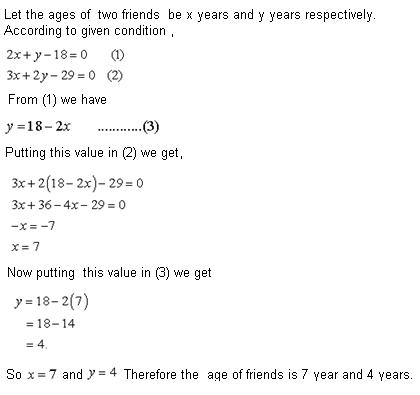
Q58. Yash
scored 40 marks in a test, getting 3 marks for each right answer and losing 1
mark for each wrong answer. Had 4 marks been awarded 4 marks for each correct
answer and 2 marks been deducted for each incorrect answer, then Yash would
have scored 50 marks. How many questions were there in the test?
Solution
Let number of correct answers be x and number
of incorrect answers be y.
As per given conditions,
3x - y = 40 …
(1)
4x - 2y = 50 …
(2)
(1) 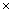 2
2 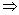 6x - 2y = 80 … (3)
Subtracting (2) from (3), we get,
2x = 30
6x - 2y = 80 … (3)
Subtracting (2) from (3), we get,
2x = 30  x = 15
y = 3x - 40 = 45 - 40 = 5
Total number of questions in the test = 15 + 5
= 20
x = 15
y = 3x - 40 = 45 - 40 = 5
Total number of questions in the test = 15 + 5
= 20
Q59. A train covered a certain distance at a
uniform speed. If the train would have been 10km/h faster, it would have
taken 2 hours less than the schedule time. And, if the trains were slower by
10km/hr, it would have taken 3 hours more than the scheduled time. Find the
distance covered by the train.
Solution
Let the original speed of train be x km/hr and
the schedule time of journey be y hours.
Therefore, s = d/t
i.e. d = xykm.
If speed of the train increases by 10km/hr, then
increased speed = (x + 10)km/hr
Time reduces by 2hrs, so reduced time = (y - 2)h
Therefore,
Distance = (x + 10)(y-2) = xy
-2x + 10y - 20
In both the cases distances are equal
xy = xy - 2x + 10y - 20
 x - 5y = -10
x - 5y = -10
 x = 5y -10
----- (1)
If
speed is reduced by 10km/hr, then the reduced speed = (x - 10)km/h
If
time is increased by 3hr, then the increased time = (y + 3)hr
Then,
distance = (x - 10)(y + 3) = xy + 3x - 10y - 30
x = 5y -10
----- (1)
If
speed is reduced by 10km/hr, then the reduced speed = (x - 10)km/h
If
time is increased by 3hr, then the increased time = (y + 3)hr
Then,
distance = (x - 10)(y + 3) = xy + 3x - 10y - 30
 xy = xy + 3x - 10y - 30
xy = xy + 3x - 10y - 30
 3x - 10y = 30 ----- (2)
Using
substitution method, subs. (1) in (2), we have
3x - 10y = 30 ----- (2)
Using
substitution method, subs. (1) in (2), we have
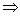 3(5y - 10) - 10y = 30
3(5y - 10) - 10y = 30
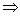 15y - 30 - 10y = 30
15y - 30 - 10y = 30
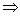 5y = 60
5y = 60
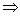 y = 12
Subs.
value of y in (1)
x
= 5(12) - 10 = 50
x
= 50
Therefore,
distance = xy = 50 x 12 = 600km
Hence,
distance covered by the train is 600km.
y = 12
Subs.
value of y in (1)
x
= 5(12) - 10 = 50
x
= 50
Therefore,
distance = xy = 50 x 12 = 600km
Hence,
distance covered by the train is 600km.
Q60. The distance of John's home from Lajpat Nagar is added to ½ the distance of his home from Sarojini Nagar,then the total distance covered is 3.5 km. And when ½ the distance of his home from Lajpat Nagar is added to 0.3 times the distance of his home from Sarojini Nagar ,the total distance covered is 1.9km. Find the distance of his home from both the places.
Solution

Q61. Solve for x and y:
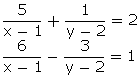
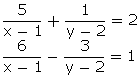
Solution
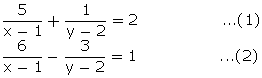 Multiply equation (1) by 3 and add in equation (2), we get,
Multiply equation (1) by 3 and add in equation (2), we get,
Q62. Draw the graph of 2x + y = 6 and 2x - y + 2 = 0. Shade the region bounded by these lines with x axis. Find the area of the shaded region.
Solution
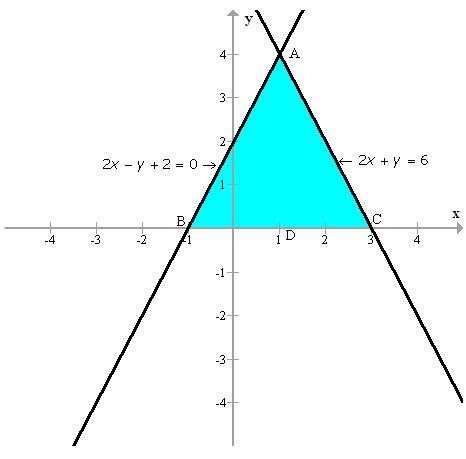 ABC is the region bounded by the given lines and the x-axis.
The solution of the given pair of equations is the point where the two lines meet which is (1, 4). Thus, x = 1 and y = 4.
Area of shaded part = Area of
ABC is the region bounded by the given lines and the x-axis.
The solution of the given pair of equations is the point where the two lines meet which is (1, 4). Thus, x = 1 and y = 4.
Area of shaded part = Area of 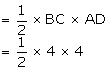 = 8 sq. units
= 8 sq. units
Q63. The
area of rectangle gets reduced by 9 m2, if length is reduced by 5
m and breadth is increased by 3 m. If we increase the length by 3 m and
breadth by 2 m, the area is increased by 67 m2. Find the length
and breadth of the rectangle.
Solution
Let
the original length be x m and breadth by y m.
Area
= xy m2
(x
- 5) (y + 3) = xy - 9
3x
- 5y = 6 ...(1)
(x
+ 3) (y + 2) = xy + 67
2x
+ 3y = 61 ...(2)
Multiplying
equation (1) with 2 and equation (2) with 3, we get
6x
- 10y = 12 ...(3)
6x
+ 9y = 183 ...(4)
On
subtracting (3) from (4), we get, y = 9
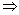 x
= 17
Hence,
Length
= 17 m
Breadth
= 9 m
x
= 17
Hence,
Length
= 17 m
Breadth
= 9 m
Q64. Solve:
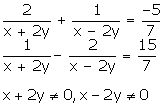
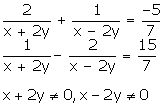
Solution
Q65. Solve
for x and y:
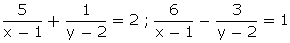
Solution
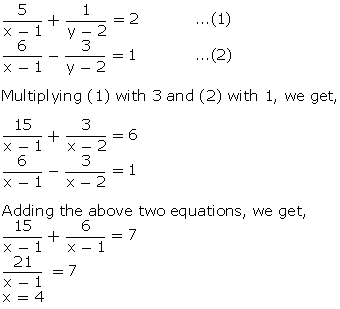 Substituting
value of x in (1), we get,
Substituting
value of x in (1), we get,
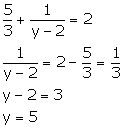
Q66. Solve : 47x + 31y = 63, 31x + 47y = 15.
Solution
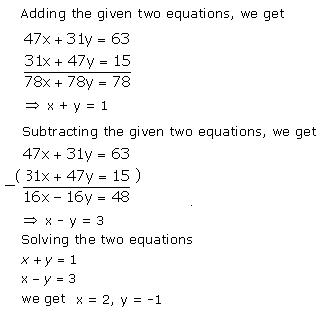
Q67. Find graphically the solution of the equations:
x + 2y = 8
y - x = 1
Also, find the co-ordinates of the points where the two lines meet y-axis.
Solution
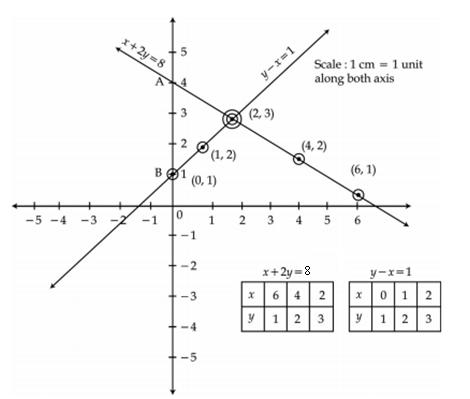 The solution of the given pair of equations is the point where the lines intersect each other.
Thus, x = 2, y = 3 is the solution of the given pair of equations.
The required co-ordinates where the lines meet the y-axis are A(0,4) and B(0,1).
The solution of the given pair of equations is the point where the lines intersect each other.
Thus, x = 2, y = 3 is the solution of the given pair of equations.
The required co-ordinates where the lines meet the y-axis are A(0,4) and B(0,1).
Q68. Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution
Let the speed of train and bus be u km/h and v km/h respectively.
According to the question,
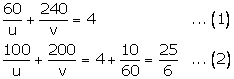 Let
Let 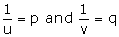 The given equations reduce to:
The given equations reduce to:
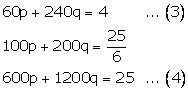 Multiplying equation (3) by 10, we obtain:
Multiplying equation (3) by 10, we obtain:
 Subtracting equation (4) from equation (5), we obtain:
Subtracting equation (4) from equation (5), we obtain:
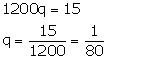 Substituting the value of q in equation (3), we obtain:
Substituting the value of q in equation (3), we obtain:
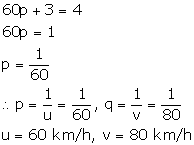 Thus, the speed of train and the speed of bus are 60 km/h and 80 km/h respectively.
Thus, the speed of train and the speed of bus are 60 km/h and 80 km/h respectively.
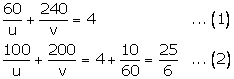 Let
Let 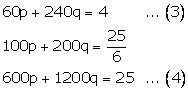 Multiplying equation (3) by 10, we obtain:
Multiplying equation (3) by 10, we obtain:
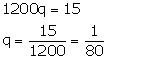 Substituting the value of q in equation (3), we obtain:
Substituting the value of q in equation (3), we obtain:
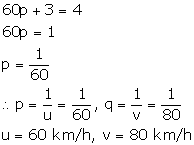 Thus, the speed of train and the speed of bus are 60 km/h and 80 km/h respectively.
Thus, the speed of train and the speed of bus are 60 km/h and 80 km/h respectively.
Q69. Solve the following system of linear equations by cross multiplication method :
2(ax - by) + (a + 4b) = 0
2(bx + ay) + (b - 4a) =0
Solution
2(ax - by) + (a + 4b) = 0
2(bx + ay) + (b - 4a) =0
The equations become:
2ax - 2by + (a + 4b) = 0
2bx + 2ay + (b - 4a) =0
By cross-multiplication method,




Q70. Is the system of linear equations 2x + 3y - 9 = 0 and 4x + 6y - 18 = 0 consistent? Justify your answer.
Solution
Comparing the given pair of linear equations with the general equations, we have,
a1 = 2, b1 = 3, c1 = -9
a2 = 4, b2 = 6, c2 = -18
It can be observed that:
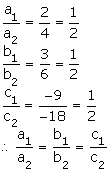 Thus, the given system of equations has infinitely many solutions and thus is consistent.
Thus, the given system of equations has infinitely many solutions and thus is consistent.
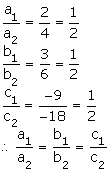 Thus, the given system of equations has infinitely many solutions and thus is consistent.
Thus, the given system of equations has infinitely many solutions and thus is consistent.
Q71. Father's
age is 3 times the sum of ages of his two children. After 5 years his age
will be twice the sum of ages of two children. Find the age of father.
Solution
Let
the age of father be x years and sum of the ages of his children by y years.
After
5 years,
Father's
age = (x + 5) years
Sum
of ages of his children = (y + 10) years
From
the given information, we have:
x
= 3y ...(1)
and
x + 5 = 2(y + 10)
 x - 2y = 15 ...(2)
From
(1) and (2), we have,
3y
- 2y = 15
x - 2y = 15 ...(2)
From
(1) and (2), we have,
3y
- 2y = 15  y = 15
y = 15
 x = 3y = 45
Father's
age = 45 years
x = 3y = 45
Father's
age = 45 years
Q72. In
the figure given below, ABCD is a rectangle. Find the values of x and y.


Solution
Since
ABCD is a rectangle, we have:
x
+ y = 22 … (1)
x
- y = 16 … (2)
Adding
(1) and (2), we get,
2x
= 38
x
= 19
So,
y = 22 - 19 = 3
Q73. Solve for u & v
2u +15v =17uv; 5u +5v= 36uv
Solution
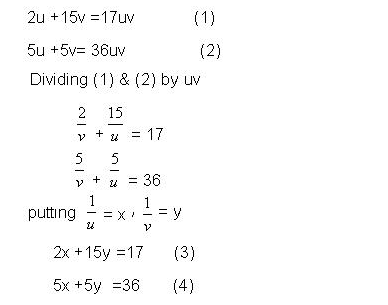 Multiply (3) by 1 2x+15y=17
Multiply (4) by 3 15x+15y=108
Multiply (3) by 1 2x+15y=17
Multiply (4) by 3 15x+15y=108
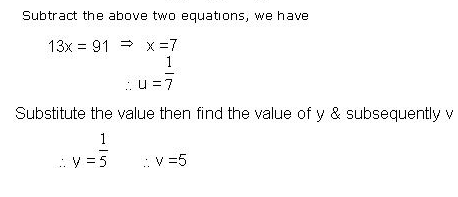
Q74. 10 years ago, mother`s age was 12 times that of her daughter and 10
years hence, her age would be twice that of her daughter. Find their present
ages.
Let the present age mother be x years and daughter's present age be y
years.
Solution
Q75. Solve the following:
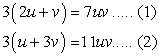
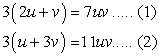
Solution
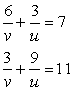 Let
Let  we get
we get
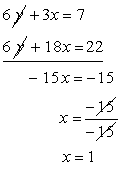 Putting this value from in (1) we get
Putting this value from in (1) we get
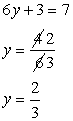 But we around that
But we around that 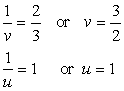
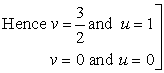 are the solution of the given equation.
are the solution of the given equation.
Q76. Two years ago a father was 5 times as old as his son, 2 years later, his age will be 8 years more than three times the age of son. Find their present ages.
Solution

Q77. Solve :
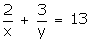
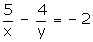 ,
,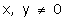
Solution
The given equations are:
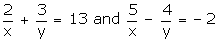 Putting
Putting  we get,
2u + 3v = 13... (1)
5u - 4v = -2... (2)
Solving (1) and (2), we get,
u = 2v= 3
Therefore,
we get,
2u + 3v = 13... (1)
5u - 4v = -2... (2)
Solving (1) and (2), we get,
u = 2v= 3
Therefore,

 we get,
2u + 3v = 13... (1)
5u - 4v = -2... (2)
Solving (1) and (2), we get,
u = 2v= 3
Therefore,
we get,
2u + 3v = 13... (1)
5u - 4v = -2... (2)
Solving (1) and (2), we get,
u = 2v= 3
Therefore,

Q78. Two women and 5 men together finish a piece of work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work and also time taken by 1 man alone to finish it.
Solution
Let one woman takes x days to finish the work.
And one man takes y days to finish the work.
According to the question,
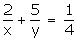 4(2y + 5x) = 1
4(2y + 5x) = 1 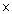 xy
8y + 20x = xy...(1)
xy
8y + 20x = xy...(1)
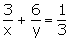 3(3y + 6x) = xy
9y + 18x = xy...(2)
3(3y + 6x) = xy
9y + 18x = xy...(2)
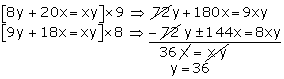
 8
8 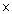 36 + 20x = 36x
36 + 20x = 36x
 = x
x = 18
= x
x = 18
 One woman takes 18 days and one man takes 36 days to finish the work.
One woman takes 18 days and one man takes 36 days to finish the work.
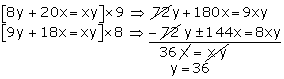
 = x
x = 18
= x
x = 18
Q79. The sum of a two digit number and the number obtained by reversing the order of its digits is 121, and the two digits differ by 3. Find the number.
Solution


Q80. For what value of p will the following system of equations have no solution
(2p - 1) x + (p - 1) y = 2p + 1; y + 3x - 1 = 0.
Solution
For no solution, we have:
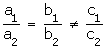 Here,
Here,
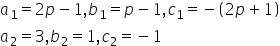
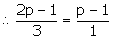 3p - 3 = 2p - 1
P = 2
3p - 3 = 2p - 1
P = 2
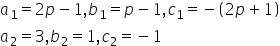
Q81. Solve:
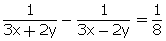
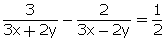 3x + 2y
3x + 2y 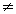 0 ; 3x - 2y
0 ; 3x - 2y 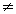 0
0
Solution
Given equations are:
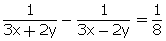 ,
, 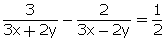 Putting
Putting  we get,
u - v =
we get,
u - v =  ...(1)
3u - 2v =
...(1)
3u - 2v =  ...(2)
Solving (1) and (2), we get,
u =
...(2)
Solving (1) and (2), we get,
u =  and v =
and v = 
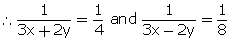 Or 3x + 2y = 4...(3)
3x - 2y = 8...(4)
Solving (3) and (4), we get,
x = 2 and y = -1
Or 3x + 2y = 4...(3)
3x - 2y = 8...(4)
Solving (3) and (4), we get,
x = 2 and y = -1
 we get,
u - v =
we get,
u - v =  ...(1)
3u - 2v =
...(1)
3u - 2v =  ...(2)
Solving (1) and (2), we get,
u =
...(2)
Solving (1) and (2), we get,
u =  and v =
and v = 
Q82. Solve the following pairs of Linear equation by substitution method 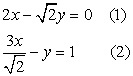
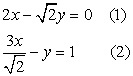
Solution

Q83. Without drawing graph, check whether the lines 3x + y = 10 and 6x - 2y = 20 are parallel or not.
Solution

Q84. Solve graphically : 4x - y = 4; 4x + y = 12
(a) Find the solution from the graph.
(b) Shade the triangular region formed by the lines and the x-axis.
Solution
4x - y = 4 ..... (i)
x
0
1
2
y
-4
0
4
4x + y = 12 ...... (ii)
x
3
2
4
y
0
4
-4
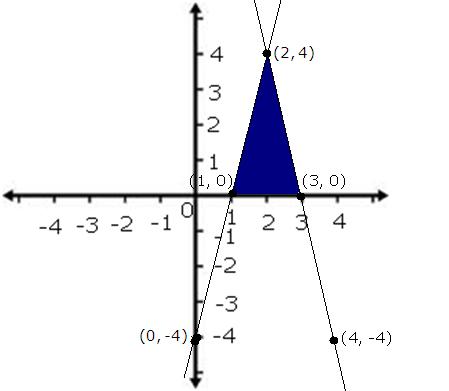 The solution of the given pair of equations will be the point where the two lines meet.
Thus, x = 2, y = 4 is the solution.
The coordinates of the vertices of the triangle formed by the lines and the x-axis are (2,4), (1,0) and (3,0).
The solution of the given pair of equations will be the point where the two lines meet.
Thus, x = 2, y = 4 is the solution.
The coordinates of the vertices of the triangle formed by the lines and the x-axis are (2,4), (1,0) and (3,0).
 The solution of the given pair of equations will be the point where the two lines meet.
Thus, x = 2, y = 4 is the solution.
The coordinates of the vertices of the triangle formed by the lines and the x-axis are (2,4), (1,0) and (3,0).
The solution of the given pair of equations will be the point where the two lines meet.
Thus, x = 2, y = 4 is the solution.
The coordinates of the vertices of the triangle formed by the lines and the x-axis are (2,4), (1,0) and (3,0).
Q85. A boat goes 16 km upstream and 24 km downstream in 6 hrs. Also it covers 12 km upstream and 36 km downstream in the same time. Find the speed of the boat upstream and downstream.
Solution
Let speed of the boat in still water = x km/hr, and
Speed of the current = y km/hr
Downstream speed = (x+y) km/hr
Upstream speed = (x - y) km/hr
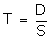
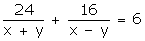 ... (1)
... (1)
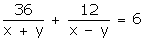 ... (2)
Putting
... (2)
Putting  the equations become:
24u + 16v = 6
Or, 12u + 8v = 3... (3)
36u + 12v = 6
Or, 6u + 2v = 1... (4)
Multiplying (4) by 4, we get,
24u + 8v = 4… (5)
Subtracting (3) by (5), we get,
12u = 1
the equations become:
24u + 16v = 6
Or, 12u + 8v = 3... (3)
36u + 12v = 6
Or, 6u + 2v = 1... (4)
Multiplying (4) by 4, we get,
24u + 8v = 4… (5)
Subtracting (3) by (5), we get,
12u = 1
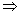 u =
u =  Putting the value of u in (4), we get, v =
Putting the value of u in (4), we get, v = 
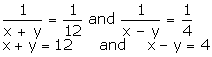 Thus, speed of the boat upstream = 4 km/hr
Speed of the boat downstream = 12 km/hr
Thus, speed of the boat upstream = 4 km/hr
Speed of the boat downstream = 12 km/hr
 the equations become:
24u + 16v = 6
Or, 12u + 8v = 3... (3)
36u + 12v = 6
Or, 6u + 2v = 1... (4)
Multiplying (4) by 4, we get,
24u + 8v = 4… (5)
Subtracting (3) by (5), we get,
12u = 1
the equations become:
24u + 16v = 6
Or, 12u + 8v = 3... (3)
36u + 12v = 6
Or, 6u + 2v = 1... (4)
Multiplying (4) by 4, we get,
24u + 8v = 4… (5)
Subtracting (3) by (5), we get,
12u = 1
 Putting the value of u in (4), we get, v =
Putting the value of u in (4), we get, v = 
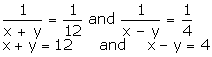 Thus, speed of the boat upstream = 4 km/hr
Speed of the boat downstream = 12 km/hr
Thus, speed of the boat upstream = 4 km/hr
Speed of the boat downstream = 12 km/hr
Q86. For what value of k, will the following pair of linear equations has no solutions ?
3x + y = 1; (2k - 1)x + (k - 1)y = 2k + 1
Solution
The given pair of linear equations are:
3x + y = 1
3x + y - 1 = 0 ...... (i)
And
(2k - 1)x + (k - 1)y = 2k + 1
(2k - 1)x + (k - 1)y - (2k + 1) = 0 ...... (ii)
We know that the pair of linear equations a1 x + b1 y +c1 = 0 and a2 x + b2 y + c2 = 0 has no solution if
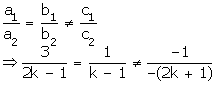
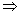 k = 2
k = 2
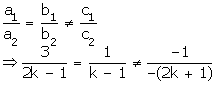
Q87. For what values of a and b, does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7; (a - b) x + (a + b) y = 3a + b - 2.
Solution
The given pair of linear equations are:
2x + 3y - 7 = 0...(1)
(a - b) x + (a + b) y - (3a + b - 2) = 0...(2)
For infinite solutions, we have
 Solving first two terms, we get,
a = 5b... (3)
Solving first and last terms, we get,
a = 9b - 4… (4)
Solving (3) and (4) we get,
a = 5, b = 1
Solving first two terms, we get,
a = 5b... (3)
Solving first and last terms, we get,
a = 9b - 4… (4)
Solving (3) and (4) we get,
a = 5, b = 1
 Solving first two terms, we get,
a = 5b... (3)
Solving first and last terms, we get,
a = 9b - 4… (4)
Solving (3) and (4) we get,
a = 5, b = 1
Solving first two terms, we get,
a = 5b... (3)
Solving first and last terms, we get,
a = 9b - 4… (4)
Solving (3) and (4) we get,
a = 5, b = 1
Q88. The sum of the
numerator and denominator of a fraction is 8. If 3 is added to both the
numerator and the denominator the fraction becomes 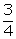 . Find the fraction.
. Find the fraction.
Solution
Let the fraction be  .
According to the question,
x + y = 8 …
(1)
.
According to the question,
x + y = 8 …
(1)
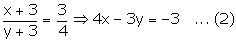 (1)
(1)  3
3 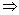 3x + 3y = 24 … (3)
Adding (2) and (3), we get 7x = 21
3x + 3y = 24 … (3)
Adding (2) and (3), we get 7x = 21 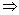 x = 3
So, y = 5
Therefore, the fraction is
x = 3
So, y = 5
Therefore, the fraction is 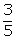 .
.
Q89. Using method of cross multiplication solve the following system of linear equations.
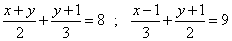
Solution

Q90. Solve graphically the pair of equations 2x + 3y = 11 and 2x - 4y = -24. Hence, find the coordinates of the vertices of the triangle formed by these lines and the x-axis.
Solution
The given pair of linear equations are:
2x + 3y = 11… (1)
2x - 4y = -24… (2)
For equation (1):
x
1
4
-2
y
3
1
5
The points (1, 3), (4, 1) and (-2, 5) can be plotted on a Cartesian plane to obtain the graph of the equation of line (1).
For equation (2):
x
-12
0
-10
y
0
6
1
The points (-12, 0), (0, 6) and (-10, 1) can be plotted on a Cartesian plane to obtain the graph of the equation of line (2).
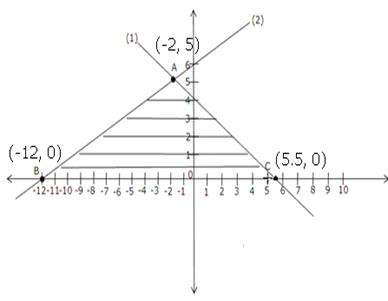 These two lines intersect each other at a point (-2, 5).
The triangle formed is shaded as
These two lines intersect each other at a point (-2, 5).
The triangle formed is shaded as  ABC. The coordinates of its vertices are A (-2,5), B (-12,0) and C(5.5,0).
ABC. The coordinates of its vertices are A (-2,5), B (-12,0) and C(5.5,0).
 These two lines intersect each other at a point (-2, 5).
The triangle formed is shaded as
These two lines intersect each other at a point (-2, 5).
The triangle formed is shaded as
Q91. Find the cost of a jacket if the cost of two
T-shirts and one jacket is Rs 625 and three T-shirts and two jackets together
costs Rs 1125.
Solution
Let the cost of one T-shirt be Rs x and that of
one jacket be Rs y.
According to given condition,
2x+y=625 …(i)
3x+2y=1125 …(ii)
Multiplying (i) by 2 we get,
4x + 2y=1250 …(iii)
Subtracting (ii) from (iii), we get,
x=125
Substituting this value of x in (i), we get,
250 + y = 625
 y=375
Therefore, cost of one T-shirt is Rs125 and the
cost of one jacket is Rs 375.
y=375
Therefore, cost of one T-shirt is Rs125 and the
cost of one jacket is Rs 375.
Q92. Rekha's mother is five times as old as her
daughter Rekha. Five years later, Rekha's mother will be three times as old
as her daughter Rekha. Find the present age of Rekha and her mother's age.
Solution
Let Rekha's age be 'x' years
And her mother's age be 'y' years
y = 5x, as per given data ---(1)
After 5 years,
y + 5 = 3(x+5)
y - 3x = 10 ----(2)
Substituting (1) in (2), we get,
2x = 10 or x = 5
So, y = 5x = 25
Hence, Rekha's age is 5 years and her mother's
age is 25 years.
Q93. From the graph given below, find whether the system of equations is consistent or not


Solution
The above pair of lines are parallel to each other and we know that the parallel lines do not intersect at any point.
So, solution of there does not exist any solution for the pair of simultaneous linear equations and hence the system of equations are inconsistent.
Q94. Represent the following system of equations graphically and hence identify the type of solution:
4x + 3y= 12; x - 3y = 9
Solution
Let's first find the respective points of both the equations which satisfies them:
4x + 3y = 12
x
0
3
y
4
0
x - 3y = 9
x
0
9
y
-3
0
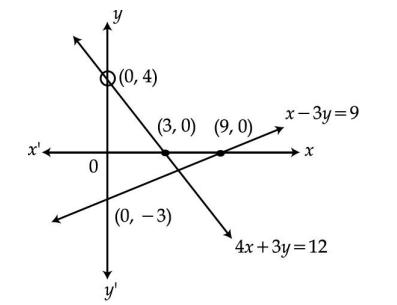 After plotting these points on the graph and joining them, we get the two lines and they interest at only one point.
Thus, the system of linear equations has unique solution and that point is
After plotting these points on the graph and joining them, we get the two lines and they interest at only one point.
Thus, the system of linear equations has unique solution and that point is  .
.
 After plotting these points on the graph and joining them, we get the two lines and they interest at only one point.
Thus, the system of linear equations has unique solution and that point is
After plotting these points on the graph and joining them, we get the two lines and they interest at only one point.
Thus, the system of linear equations has unique solution and that point is  .
.
Q95. Represent the system of equations 4x - y = 4 and 4x + y = 12 graphically. Determine the vertices of the triangle formed by these lines and the x-axis. Shade the triangular region so formed.
Solution

Q96. Using method of cross multiplication solve the following system of linear equations.
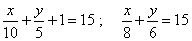
Solution
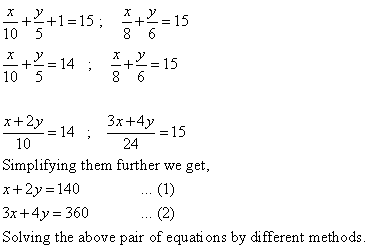

Q97. Ritu can row
downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of
rowing in still water and the speed of the current.
Solution
Let the speed of Ritu in still water and the
speed of stream be x km/h and y km/h respectively.
Speed of Ritu while rowing upstream = (x - y) km/h
Speed of Ritu while rowing downstream =(x + y)
km/h
According to the question,
 Adding equations (1) and (2), we obtain:
Adding equations (1) and (2), we obtain:
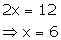 Putting the value of x in equation (1),
we obtain:
y = 4
Thus, Ritu's speed in still water is 6 km/h and
the speed of the current is 4 km/h.
Putting the value of x in equation (1),
we obtain:
y = 4
Thus, Ritu's speed in still water is 6 km/h and
the speed of the current is 4 km/h.
 Adding equations (1) and (2), we obtain:
Adding equations (1) and (2), we obtain:
Comments
Post a Comment