Q1. The probability that a leap year has 53 Sundays is
-
1)
-
2)
-
3)
-
4)
Solution
Number of days in a leap year = 366 = 52 weeks + 2 days
In 52 weeks, there are 52 Sundays.
Now, the remaining 2 days can be:
Sunday and Monday
Monday and Tuesday
Tuesday and Wednesday
Wednesday and Thursday
Thursday and Friday
Friday and Saturday
Saturday and Sunday
So, clearly there are a total of 7 possibilities.
The leap year will have 53 Sundays if the last two days of the year are either Sunday and Monday or Saturday and Sunday.
Thus, favorable outcomes = 2
Hence, Required Probability = 
Q2. A pair of dice are thrown once. Find the probability of getting the same number (doublet) on each dice.
Solution
When the dice are thrown, the number of out comes are as follows:
1, 1
1, 2
1, 3
1, 4
1, 5
1, 6
2, 1
2, 2
2, 3
2, 4
2, 5
2, 6
3, 1
3, 2
3, 3
3, 4
3, 5
3, 6
4, 1
4, 2
4, 3
4, 4
4, 5
4, 6
5, 1
5,2
5, 3
5, 4
5, 5
5, 6
6, 1
6, 2
6, 3
6, 4
6, 5,
6, 6
Hence, the total number of outcomes = 36
There are 6 ways of obtaining the same number on each dice which are
(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
Q3. Find
the probability that a non leap year chosen at random has
(i) 52
Sundays (ii) 53 Sundays
Solution
Non
leap year has 365 days
i.e.,
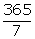= 52 weeks and
1 day.
If
this one day is not Sunday, then year will have 52 Sundays, so then the probability
of 52 Sundays = 
(as
that one day can be Mon, Tue, Wed, Thu, Fri, Sat)
Probability
of 53 Sundays = 
(as
that one day can be Sunday)
= 52 weeks and
1 day.
If
this one day is not Sunday, then year will have 52 Sundays, so then the probability
of 52 Sundays =
(as
that one day can be Mon, Tue, Wed, Thu, Fri, Sat)
Probability
of 53 Sundays =
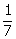(as
that one day can be Sunday)
Q4. A game consists of tossing a one rupee coin three times and noting its outcome each time. Ramesh wins if all the tosses give the same result, that is three heads or three tails and loses the game otherwise. Calculate the probability that Ramesh will lose the game.
Solution
Q5. The probability of getting a prime number in single throw of a dice is:
-
1)
- 2) Zero
-
3)
-
4)
Solution
When a dice is thrown, the possible outcomes are {1, 2, 3, 4, 5, 6}.
Prime numbers = {2, 3, 5}
Required probability = 
Required probability =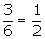
Q6. A bag
contains cards numbered from 2 to 26. One card is drawn from the bag at
random. Find the probability that it has a number divisible by both 2 and 3.
Solution
Nos.
divisible by both 2 and 3 in between 2 and 26 are 6, 12, 18, 24
Total
no. of cards = 25
P(no.
divisible by both 2 and 3) =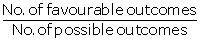 
= 
=
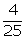
Q7. Two dice are thrown together. Find the
probability that the product of the numbers on the top of the dice is
(i) 6
(ii) 12
(iii) 7
Solution
Total
outcomes = 36
Q8. Which one of the following cannot be the probability of an event?
Solution
We know that the probability of an event always lies between 0 and 1. Thus, 1.1 cannot be the probability of any event.
Q9. A bag
contains 2 green, 3 red and 4 black balls. A ball is taken out of the bag at
random. Find the probability that the selected ball is (i) not green (ii) not
black.
Solution
Total
number of balls =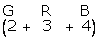 
= 9
= 9
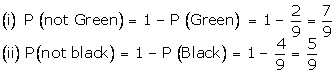
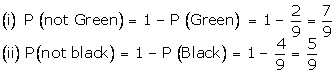
Q10. A bag
contains 5 red balls and some blue balls. If the probability of drawing a
blue ball from the bag is four times that of a red ball, find the number of
blue balls in the bag.
Solution
Let
x be the number of blue balls.
Number
of red balls = 5
Total
number of balls = 5 + x
P
(red ball) =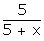 
P
(blue ball) = 
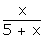
Number of blue balls = 20
P
(blue ball) =
Number of blue balls = 20
Q11. A bag
contains 14 balls of which x are white. If 6 more white balls are added to
the bag, the probability of drawing a white ball is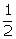
. Find the value of x.
. Find the value of x.Solution
Total
number of balls = 14
Number
of white balls = x
When
6 more white balls are added, then,
Total
number of balls = 14 + 6 = 20, Number of white balls = 6 + x
P
(drawing white ball) = 
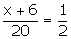(Given)
2x
+ 12 = 20
2x
= 8
x
= 4
(Given)
2x
+ 12 = 20
2x
= 8
x
= 4
Q12. Two coins are tossed simultaneously. Find the probability of getting (i) Two heads (ii) At least one head (iii) No head.
Solution
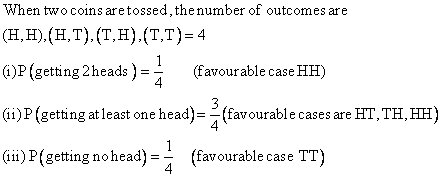
Q13. Two coins are tossed together. The probability of getting head on both the coins is
- 1) 0
-
2)
-
3)
-
4)
Solution
When two coins are tossed together, outcomes are = {HH, HT, TH, TT}
Thus, total number of possible outcomes = 4
Number of Favourable outcomes = 1 {HH}
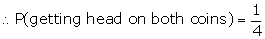
Q14. If the probability of winning a game is 0.995, then the probability of losing is
Solution
P(losing the game) = 1 - P(winning the game)
= 1 - 0.995
= 0.005
Q15. An urn
contains 8 red, 6 white, 4 black balls. A ball is drawn at random from the
urn. Find the probability that the drawn ball is
(i)
Red or white (ii) Neither black
nor white
Solution
Total
number of balls in the urn =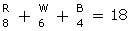 
P
(Red or white) = 
P(neither
black nor White) = 1 - 
P(neither
black nor White) = 
P
(Red or white) =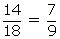
P(neither
black nor White) = 1 -
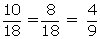P(neither
black nor White) =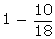
Q16. If a letter of English alphabet is chosen at random, then the probability that the letter is a consonant is:
-
1)
-
2)
-
3)
-
4)
Solution
Number of letters in English alphabet = 26
Number of consonants = 21
Required probability = 
Required probability =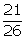
Q17. Two dice are thrown simultaneously. Probability of getting a prime number on both the dice is:
-
1)
-
2)
-
3)
-
4)
Solution
Prime numbers in one dice = 2, 3, 5
Possibilities of occurrence of prime numbers in both dices:
(2,2),(2,3),(2,5),(3,2),(3,3), (3,5),(5,2),(5,3),(5,5)
Total number of possibilities from the above = 9
Total number of outcomes = 36
The probability of getting a prime number on both dice=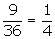
Q18. From a
well shuffled pack of 52 cards, two black kings and two black jacks are
removed. From the remaining cards, a card is drawn at random. Find the
probability that the drawn card is not a king.
Solution
Number
of cards removed = 4
Number
of cards left = 52 - 4 = 48
Number
of kings in 48 cards = 2
P
(drawing a king) = 
Required probability = 
Number
of cards left = 52 - 4 = 48
Number
of kings in 48 cards = 2
P
(drawing a king) =
Required probability =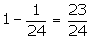
Q19. From a deck of playing cards all aces and
clubs are removed, a card is drawn at random from the remaining cards. Find
the probability that it is:
(a) A black face card.
(b) A red card
Solution
Total number of cards = 52
All aces and clubs are removed.
Remaining number of cards = 52 -
16 = 36
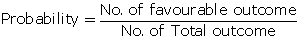(a) Number of black face cards
left = 3
(b) Number of red cards left = 24
(a) Number of black face cards
left = 3
(b) Number of red cards left = 24
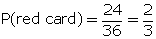
Q20. A bag contains 5 black, 7 red and 3 white
bells. A ball is drawn from the bag at random. Find the probability that the
ball drawn is
(a) Black or white
(b) Not black
Solution
Total
number of balls in the bag = 5 + 7 + 3 = 15
(i)
P(Black or White) =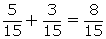 
(ii)
P(not black) = 1 - P(back ball) = 
(ii)
P(not black) = 1 - P(back ball) =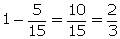
Q21. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is thrice that of a red ball, find the number of blue balls in the bag.
Solution
Q22. A card
is drawn at random from a pack of well shuffled deck of playing cards. Find
the probability that the card is
(i) a
king or a jack (ii) a card of
spade or an ace
Solution
Total
no. of outcomes = 52
(i)
Favourable outcomes = 4 + 4 = 8
P (a king or jack) = 8/52
= 2/13
(ii)
Favourable outcomes = 13 + 4 - 1
= 16
P(a spade or an ace) = 16/52
= 4/13
Q23. A box contains 90 discs which are numbered
from 1 to 90. If one disc is drawn at random from the box, find the
probability that it bears
(i) A two-digit number.
(ii) A perfect square number.
(iii) A number divisible by 5.
Solution
Total
outcomes = 90
(i)
Two digit numbers are from 10 to 90 which are 81 in number.
P(getting
a two-digit number) = 
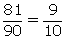(ii)
Perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 84.
P(getting a perfect square) =
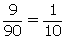(iii)
Numbers divisible by 5 are 5, 10, .... , 90, which are 18 in number.
P(getting
a number which is divisible by 5) = 
P(getting
a two-digit number) =
(ii)
Perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 84.
P(getting a perfect square) =
(iii)
Numbers divisible by 5 are 5, 10, .... , 90, which are 18 in number.
P(getting
a number which is divisible by 5) =
Q24. Three unbiased coins are simultaneously tossed. What is the probability of getting exactly two heads?
Solution
In tossing 3 coins simultaneously, the possible outcomes are
{HHH, HHT, HTH, THT, THH, TTH, THT, HTT, TTT}
Thus, number of outcomes = 8
Let A be the event of getting exactly two heads.
Thus, number of favourable outcomes = {HHT, HTH, THH} = 3
Hence, P(A) = 
Q25. King, queen and jack of hearts are removed from a pack of 52 playing cards and then the pack is well shuffled. A card is drawn from the remaining cards. Find the probability of getting a card of
(i) hearts (ii) a queen (iii) not a king
Solution
When king, queen and jack of hearts are removed, number of cards remaining = 52 - 3 = 49
Total no. of outcomes = 49
(i) Let A be the event of getting a heart card.
Thus, favourable outcomes = 10 (3 hearts are removed)
(ii) Let B be the event of getting a queen card.
Thus, favourable outcomes = 3 (1 queen is removed)
(iii) Let C be the event of not getting a king card.
Thus, out of 49 cards, there are 3 king cards.
Hence, favourable outcomes = 46
(ii) Let B be the event of getting a queen card.
Thus, favourable outcomes = 3 (1 queen is removed)
(iii) Let C be the event of not getting a king card.
Thus, out of 49 cards, there are 3 king cards.
Hence, favourable outcomes = 46
Q26. Two dice are thrown at the same time. Find
the probability of
(i) Same number one both the dice
(ii) Different number on both the dice.
Solution
When
two dice are thrown, the total number of possible outcomes is 36.
(i)
Favourable outcomes = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
Required probability = 
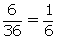(ii)
Required probability = 1 - P(getting same number on both the dice)
= 1 - 
= 
Required probability =
(ii)
Required probability = 1 - P(getting same number on both the dice)
= 1 - =
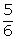
Q27. A box contains 12 balls out of which x are
black. If one ball is drawn at random from the box, what is the probability
that it will be a black ball? If 6 more black balls are put in the box, the
probability of drawing a black ball now is double of what it was before. Find
x.
Solution
Total
number of balls = 12
Let
the number of black balls be x.
P(drawing
a black ball) =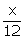 
It
is given that 6 more black balls are put in the box.
Now,
we have:
Total
number of balls = 18
Number
of black balls = x + 6
P
(drawing a black ball) = 
Therefore,
we have:
It
is given that 6 more black balls are put in the box.
Now,
we have:
Total
number of balls = 18
Number
of black balls = x + 6
P
(drawing a black ball) =
Therefore,
we have:
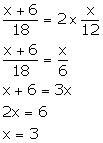
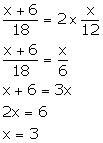
Q28. From a pack of 52 playing cards – jacks, queens, kings and aces of red colour are removed. From the remaining, a card is drawn at random. Find the probability that the card drawn is (i) a black queen (ii) a red card (iii) a face card.
Solution
Q29. A game
of chance consists of spinning an arrow which comes to rest pointing at one
of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes.
What is the probability that it will point at
(i) a
prime number (ii) a factor
of 8
Solution
Total
number of outcomes = 8
(i)
Prime numbers are = 2,3,5,7
P (prime number) = 4/8 = ½
(ii)
Factors of 8 = 1,2,4,8
P(factor of 8) = 4/8
= 1/2
Q30. Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on
(i) the same day?
(ii) Different day? (iii) On consecutive days?
Solution
Q31. There are 30 cards numbered from 1 to 30. One card is drawn at random. Find the probability that the number of the selected card is not divisible by 3.
Solution
Total number of outcomes = 30
Numbers which are not divisible by 3 are 1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26, 28, 29
Thus, number of favourable outcomes = 20
Hence, P(Number is not divisible by 3) = 
Q32. All
the face cards of spades are removed from a pack of 52 playing cards and then
the pack is shuffled well. A card is then drawn at random from the remaining
pack of cards. Find the probability of getting (i) a black face card, (ii) a
queen.
Solution
Total
cards = 52
Three
face cards of spades are removed.
Total cards left = 49
P
(Black face card) =
.
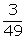P(Queen)
= .
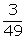(as
total black face cards are now 3, instead of 6 and total queens are 3 instead
of 4)
Total cards left = 49
P
(Black face card) =.
P(Queen)
= .
(as
total black face cards are now 3, instead of 6 and total queens are 3 instead
of 4)
Q33. Cards
numbered from 1 to 64 are placed in a box. A card is drawn at random from the
box. Find the probability that the card number on the card drawn is a perfect
cube.
Solution
Total
number of outcomes = 64
Let
E be the event of drawing a card with number as a perfect cube on it.
Number
of favourable outcomes = {1, 8, 27, 64}
n(E)
= 4
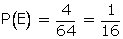
Q34. From a bag containing 5 red, 6 black and 7
yellow balls, a ball is drawn at random. Find the probability that it is:
(a) Not yellow ball
(b) Neither black nor red
(c) Either black or yellow
Solution
Total
number of balls = 5 + 6 + 7 = 18
(a)
P(not yellow ball) =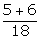 
= 
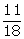(b)
P(neither black nor red ball) = P(yellow ball) = 
(c)
P(either black or yellow ball) = 
= 
=
(b)
P(neither black nor red ball) = P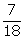(yellow ball) =
(c)
P(either black or yellow ball) = =
Q35. Two
coins are tossed together. Find the probability of getting at least one tail.
Solution
Total
possibilities = {HH, HT, TH, TT}
Number
of possible outcomes = 4
Favourable
outcomes = {HT, TH, TT}
Number
of favourable outcomes = 3
P(at least one tail) = 
P(at least one tail) =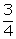
Q36.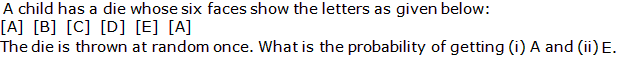 
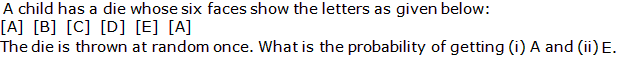
Solution
Total outcomes = 6
Number of A's = 2
Thus, P(getting A) = 
Number of E's = 1
Thus, P(getting E) = 
Number of E's = 1
Thus, P(getting E) =
Q37. Cards, marked with numbers 5 to 50, are placed in a box and mixed thoroughly. A card is drawn from the box the at random. Find the probability that the number on the card taken is (i) a prime number less than 10. (ii) a number which is perfect square.
Solution
Q38.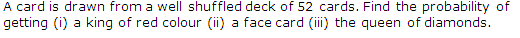 
Solution
Q39. A bag
contains 19 cards, bearing numbers 1,2,3, ......, 19. A card is drawn at
random from the bag. Find the probability that number on the drawn card is
(i)
Prime (ii) Divisible by 3.
Solution
Total
number of cards = 19
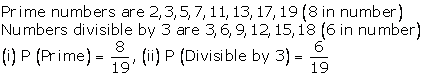
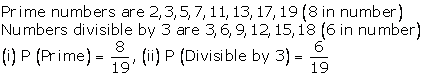
Q40. In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize?
Solution
Q41. Three coins are tossed simultaneously. Find the probability of getting
(a) three heads
(b) exactly 2 heads
(c) at least 2 heads.
Solution
Three coins are tossed simultaneously.
Possible outcomes = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
Number of total outcomes = 8
(a) Let A be the event of getting three heeds
Thus, possible outcomes = {HHH} = 1
P(three heads) = 
(b) Let B be the event of getting exactly two heeds
Thus, possible outcomes = {HHT, HTH, THH} = 3
P(exactly 2 heads) =
(c) Let A be the event of getting at least two heeds
Thus, possible outcomes = {HHH, HHT, HTH, THH} = 4
P(at least 2 heads) = 
P(three heads) =
(b) Let B be the event of getting exactly two heeds
Thus, possible outcomes = {HHT, HTH, THH} = 3
P(exactly 2 heads) =
(c) Let A be the event of getting at least two heeds
Thus, possible outcomes = {HHH, HHT, HTH, THH} = 4
P(at least 2 heads) =
Comments
Post a Comment