11

Q1. In drawing triangle ABC, it is given that AB = 3 cm, BC = 2 cm and AC = 6 cm. It is not possible to draw the triangle as:

• 1) AB > BC
• 2) AB < AC + BC
• 3) AB < AC
• 4) AC > AB + BC

Solution

We know that in a triangle, sum of two sides is greater than the third side. Here, AB + BC = 5 cm and AC = 6 cm So, we have: AC > AB + BC Thus, it is not possible to construct triangle ABC with given measurements.

Q2. Construct a triangle whose perimeter is 13.5 cm and the ratio of the three sides is 2: 3: 4.

Solution

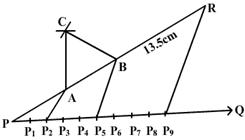Steps of construction.   1.Draw a line segment PR of length 13.5 cm. 2. At the point P draw ray PQ making any acute angle RPQ with Pr. 3. On PQ mark 9 (2+3+ 4) points P₁, P₂, P₃,  P_4, P_5, P₆,  P₇,  P₈, P₉ such that PP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅ = P₅P₆ = P₆P₇ = P₇P₈ = P₈P₉. 4. Join P₉R. 5. Through P₂ and P₅  draw ray P₂A and P₅B respectively parallel to  P₉R intersecting PR at A and B respectively. 6. With A as centre and radius AP draw an arc. 7. With B as centre draw another arc to intersect the arc of step 6 at C. 8. Join CA and CB. Then ABC is the required triangle.

Q3. Draw a pair of tangent to a circle of radius 5 cm which are inclined to each other at an angle of 60^o.

Solution

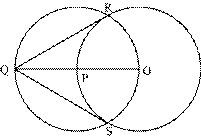
Rough figure: Consider the given figure PQ and PR are the tangents to the given circle. If they are inclined at 60^o, then 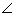QPO = 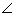OPR = 30^o Hence 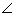POQ = 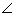POR = 60^o Consider QSO 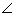QOS = 60^o OQ = OS (radius) So, 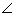OQS = 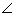OSQ = 60^o QSO is an equilateral triangle So QS = SO = QO = radius PQS = 90° - OQS = 90^o - 60^o = 30^o QPS = 30^o PS = SQ (isosceles triangle) Hence PS = SQ = OS (radius) Now we may draw tangents on the circle as following: 1. Draw a circle of 5 cm radius and with centre O. 2. Take a point P on circumference of this circle. Extend OP to Q such that OP = PQ. 3. Midpoint of OQ is P. Draw a circle with radius OP with centre as P. Let it intersect our circle at R and S. Join QR and QS. QR and QS are required tangents.

Q4. Construct an isosceles triangle whose base is 5cm and altitude 4 cm. then another triangle whose sides are one and a half times the corresponding sides of the isosceles triangle.

Solution

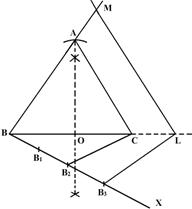Steps of construction:   i. Draw line segment BC = 5 cm. Construct the perpendicular bisector of BC, on the upper side of BC mark a point A at a distance of 4 cm. ii. Join AB and AC to get isosceles triangle ABC. iii. Draw any ray BX making an acute angle with BC on the side opposite to the vertex A. iv. Locate three points B_1, B₂ and B₃ on BX such that BB₁ = B₁B₂ = B₂B₃. v. Join B₂ (smaller of 3/2) to C. vi. Draw a line through B₃ parallel to B₂C, intersecting the extended line segment BC to L vii. Draw a line through L parallel to CA intersecting the extended line segment BA to M viii. Then MBL is the required triangle.

Q5. Draw two tangents to a circle of radius 3.5 cm from a point P at a distance of 6 cm from its centre O.

Solution

Steps of construction: 1. Take any point O of the given plane as centre draw a circle of 3.5 cm radius. Locate a point P, 6 cm away from O. Join OP. 2. Bisect OP. Let M be the midpoint of PO. 3. Taking M as centre and MO as radius draw a circle. 4. Let this circle intersect our circle at point Q and R. 5. Join PQ and PR. PQ and PR are the required tangents.

Q6. Draw a circle of diameter 5.8 cm. Draw one of its diameter. Through one of the end points of the diameter, construct tangent to the circle.

Solution

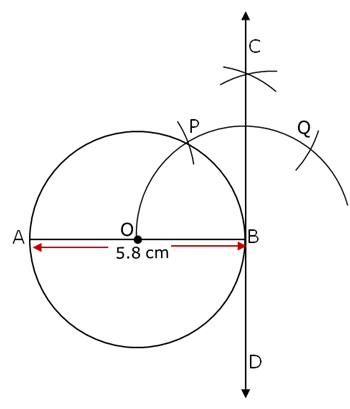
Q7. Construct a right triangle ABC in which BC = 12 cm, AB = 5 cm and A = 90°. Construct a triangle similar to it and of scale factor .

Solution

Steps of construction are as follows: 1. Draw a line segment AB = 5 cm. At point A construct a right angle SAB. 2. Draw an arc of radius 12 cm with B as its centre to intersect SA at C. Join BC to obtain ABC. 3. Draw a ray AX making an acute angle with AB, opposite to vertex C. 4. Locate 3 points A₁, A₂, A₃ on line segment AX such that AA₁ = A₁A₂ = A₂A₃. 5. Join A₃B. Draw a line through A₂ parallel to A₃B intersecting AB at B'. 6. Through B', draw a line parallel to BC intersecting AC at C'. AB'C' is the required triangle.

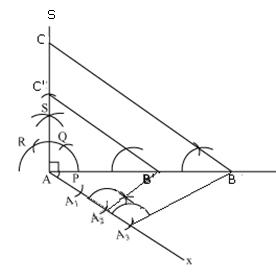
Q8. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.

Solution

Q9. Construct a triangle similar to ABC in which AB = 4.6 cm, BC = 5.1 cm, 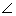A = 60^o with scale factor 4: 5.

Solution

Steps of construction :- (1) Draw a line segment AB of 4.6 cm. (2) At B draw an angle of 60^o. (3) With centre B and radius 5.1 cm draw an arc which intersect line of angle at C. (4) Join BC. (5) At A draw an angle BAX of any measure. (6)Starting from A, cut 5 equal parts on Ax. (7) Join x₅B (8) Through x₄, Draw x₄Q || x₅B (9) Through Q, Draw AP || BC

Q10. Construct a triangle ABC in which BC = 5cm, angle B = 75^o and the median bisecting BC is 3.6 cm.

Solution

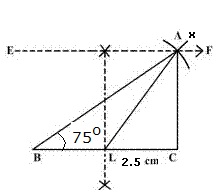Steps of construction. i. Draw a line segment BC = 5 cm. ii. Construct angle CBX = 75^o. iii. Bisect BC at L. iv. With L as centre and radius 3.6 cm draw an arc cutting BX at A v. Join AC. vi. Then triangle ABC is the required triangle.

Q11. In the figure, P divides AB internally in the ratio:

• 1) 3 : 7
• 2) 4 : 3
• 3) 3 : 4
• 4) 4 : 7

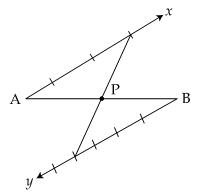
Solution

P divides AB internally in the ratio 3 : 4.

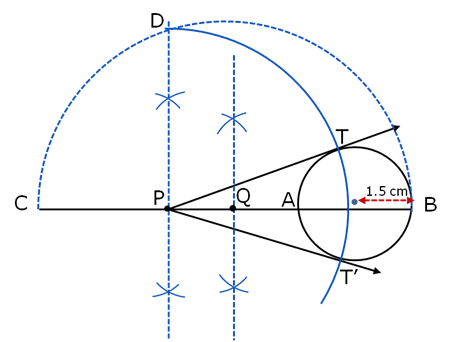
Q12. Draw a circle of radius 1.5 cm. Take a point P outside it. Without using the centre, draw two tangents to the circle from the point P.

Solution

   

Q13. Construct a triangle similar to a given isosceles triangle PQR with QR = 6 cm, PR = PQ = 5cm such that each of its sides is six- seventh of the corresponding sides of triangle PQR.

Solution

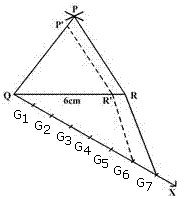Steps of construction;  

Q14.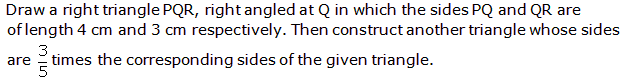

Solution

Q15. Given a triangle with side AB = 8 cm. To get a line segment AB' = 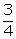of AB, it is required to divide the line segment AB in the ratio:

• 1) 1 : 3
• 2) 3 : 1
• 3) 4 : 3
• 4) 3 : 4

Solution

Q16. Construct a tangent to circle of radius 4 cm through a point P on its circumference.

Solution

      Steps of construction. i. Draw a circle with centre O and radius = 4 cm ii. Take a point P on the circumference of the circle. iii. Join OP iv. Construct angle OPA = 90^o and extend AP to B v. Then APB is the required tangent to the circle.

Q17. Construct a ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Then, construct a triangle ABC such that .

Solution

A triangle ABC is to be constructed such that . This means that the triangle ABC is similar to the triangle ABC with scale factor as The steps of construction are as follows: 1. Draw a line segment BC = 5 cm. 2. With B as centre and radius = AB = 4 cm, draw an arc. 3. With C as centre and radius = AC = 6 cm, draw another arc, meeting the arc drawn in step 2 at the point A. 4. Join AB and AC to obtain ABC. 5. Below BC, make an acute angle CBX. 6. Along BX mark off three points B₁, B₂ , B₃ such that BB₁ = B₁B₂ = B₂B₃. 7. Join B₃C. 8. From B₂, draw B₂C || B₃C. 9. From C, draw CA _|| CA, meeting BA at the point A. Then ABC is the required triangle.  

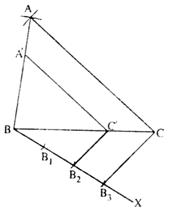
Q18.

Solution

Q19. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and 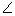ABC = 60°. Then construct a triangle whose sides are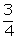of the corresponding sides of the triangle ABC.

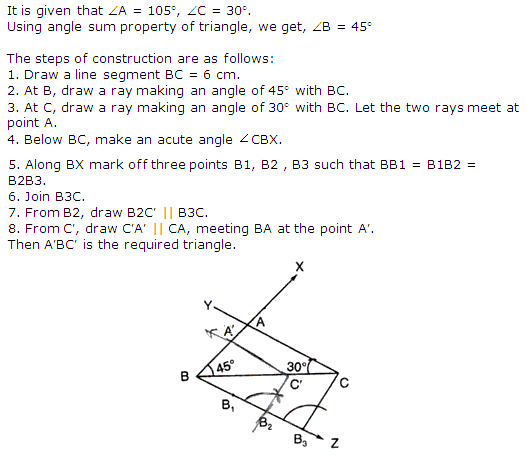
Solution

Following steps will be followed to draw a triangle A'BC' whose sides are 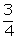of corresponding sides of ABC. 1. Draw a line segment BC of 6 cm. Draw an arc of any radius while taking B as centre. Let it intersect line BC at point O. Now taking O as centre draw another arc to cut the previous arc at point O'. Joint BO' which is the ray making 60° with line BC. 2. Now draw an arc of 5 cm. radius, while taking, B as centre, intersecting extended line segment BO' at point A. Join AC. DABC is having AB = 5 cm. BC = 6 cm and 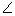ABC = 60°. 3. Draw a ray BX making an acute angle with BC on opposite side of vertex A. 4. Locate 4 points (as 4 is greater in 3 and 4). B₁, B₂, B₃, B₄ on line segment BX. 5. Join B₄C and draw a line through B₃, parallel to B₄C intersecting BC at C'. 6. Draw a line through C' parallel to AC intersecting AB at A'. DA'BC' is the required triangle.