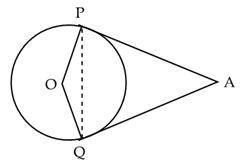
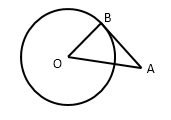
Q1. In the figure, AP and AQ are tangents to the circle with centre O, from an external point A. If  PAQ = 70o then
PAQ = 70o then  APQ is equal to:
APQ is equal to:

Solution
We know that tangents from an external point to the circle are equal.
So, AP = AQ
 AQP =
AQP = 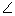 APQ
In
APQ
In 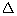 APQ,
APQ,
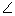 APQ +
APQ + 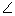 AQP +
AQP + 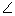 PAQ = 180o
2
PAQ = 180o
2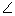 APQ = 180o - 70o(
APQ = 180o - 70o(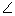 PAQ = 70o)
2
PAQ = 70o)
2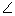 APQ = 110o
APQ = 110o
 APQ = 55o
APQ = 55o
Q2. In
fig., PT and PS are tangents to a circle from a point P such that PT = 5 cm
and  TPS = 60o. Find the length of chord TS.
TPS = 60o. Find the length of chord TS.
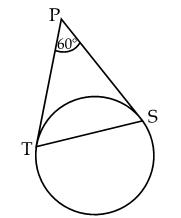

Solution
We
know that the lengths of the tangents drawn from an external point are equal.
 PT
= PS
PT
= PS 
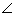 PTS =
PTS = 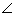 PST
Using
angle sum property,
PST
Using
angle sum property,
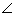 PTS +
PTS + 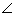 PST + 60o = 180o
PST + 60o = 180o
 2
2  PST= 120o
PST= 120o


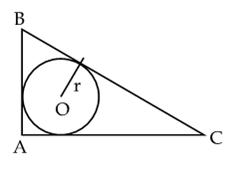
Q3. In a right triangle ABC, right angled at B, BC = 15 cm, and AB = 8 cm. A circle is inscribed in triangle ABC. The radius of circle is :
Solution
Let r be the radius of the incircle.
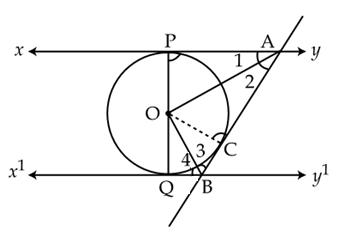
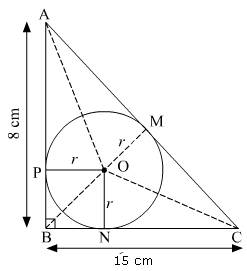 AB, BC and CA tangents to the circle at P, N and M.
AB, BC and CA tangents to the circle at P, N and M.
 OP = ON = OM = r (radius of the circle)
Area of
OP = ON = OM = r (radius of the circle)
Area of  ABC =
ABC = 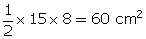 By Pythagoras theorem,
CA2 = AB2 + BC2 = 82 + 152 = 289
By Pythagoras theorem,
CA2 = AB2 + BC2 = 82 + 152 = 289
 CA = 17 cm
Area of
CA = 17 cm
Area of 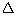 ABC = Area
ABC = Area 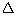 OAB + Area
OAB + Area 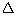 OBC + Area
OBC + Area 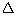 OCA
OCA
 Thus, the radius of the incircle is 3 cm.
Thus, the radius of the incircle is 3 cm.
 AB, BC and CA tangents to the circle at P, N and M.
AB, BC and CA tangents to the circle at P, N and M.
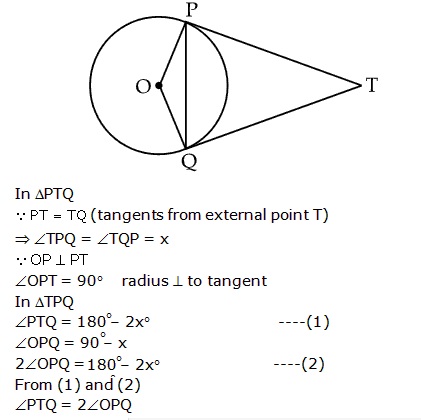
 Thus, the radius of the incircle is 3 cm.
Thus, the radius of the incircle is 3 cm.
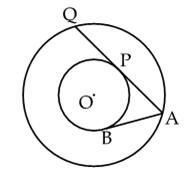
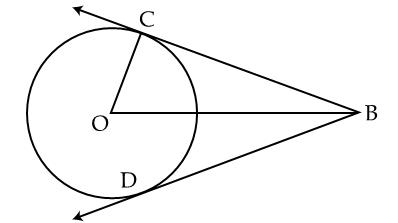
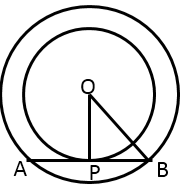
Q4. The figure shows two concentric circles with centre O. AB and APQ are tangents to the inner circle from point A lying on the outer circle. If AB = 7.5 cm then AQ is equal to:

Solution
 AB = AP……Length of tangents from an external point on a circle are equal.
AP = AB = 7.5 cm
Also, AQ is the chord to the outer circle.
Therefore, OP is the perpendicular bisector to AQ.
OP
AB = AP……Length of tangents from an external point on a circle are equal.
AP = AB = 7.5 cm
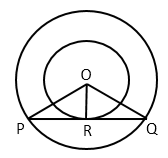
Also, AQ is the chord to the outer circle.
Therefore, OP is the perpendicular bisector to AQ.
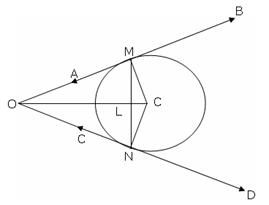
OP  AQ = 2AP = 2 X 7.5 cm = 15 cm
AQ = 2AP = 2 X 7.5 cm = 15 cm
Q5. In
fig., AB = 12 cm, BC = 8 cm and AC = 10 cm. Find AD, BE and CF.


Solution
The
lengths of the tangent drawn from an external point are equal. Therefore, we
have:
AD
= AF = x1
BD
= BE = x2
CE
= CF = x3
AB
= x1 + x2 = 12 cm
BC
= x2 + x3 = 8 cm
CA
= x1 + x3 = 10 cm
On
adding,
AB
+ BC + CA = 2(x1 + x2 + x3) = 12 + 8 + 10
 x1 + x2 + x3
= 15
Therefore, we get:
x2
= 15 - 10 = 5
x1
= 12 - 5 = 7
x3
= 10 - 7 = 3
x1 + x2 + x3
= 15
Therefore, we get:
x2
= 15 - 10 = 5
x1
= 12 - 5 = 7
x3
= 10 - 7 = 3
 AD
= x1 = 7 cm, BE = x2 = 5 cm, CF = x3 = 3 cm
AD
= x1 = 7 cm, BE = x2 = 5 cm, CF = x3 = 3 cm
Q6. In fig., two concentric circles of radii a and b (a > b) are given. The chord AB of larger circle touches the smaller circle at C. The length of AB is:
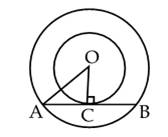

Solution
We know that radius is perpendicular to the tangent at the point of contact.
 Given, OA = a and OC = b
Now, In right triangle AOC, we have:
AC2 = OA2 - OC2 = a2 - b2
AC =
Given, OA = a and OC = b
Now, In right triangle AOC, we have:
AC2 = OA2 - OC2 = a2 - b2
AC = 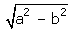 Now, we know that perpendicular drawn through the centre (O) to a chord (AB) bisects the chord.
Now, we know that perpendicular drawn through the centre (O) to a chord (AB) bisects the chord.

Q7. 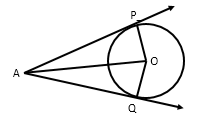 ∆OPA
and ∆OQA are congruent by the ____ test.
∆OPA
and ∆OQA are congruent by the ____ test.
 ∆OPA
and ∆OQA are congruent by the ____ test.
∆OPA
and ∆OQA are congruent by the ____ test.Solution
In ∆OPA and ∆OQA,
∠APO = ∠AQO = 90° … (tangent ⊥ radius)
AO is common and is the hypotenuse.
OP = OQ … (radius)
So, ∆OPA and ∆OQA are congruent by the RHS test.
Q8. How many tangents can be drawn from an external point
to a circle?
Solution
Two tangents can be drawn from an external point to a circle.
Q9. From the given figure, ∠TPQ and ∠TOQ are
Solution
∠TPQ and ∠TOQ are complementary angles as ∠OTP =∠OQP = 90°.
Q10. The ___ at any point on the circle is perpendicular to
the radius through the point of contact.
Solution
The tangent at any point on the circle is
perpendicular to the radius through the point of contact.
Q11. The length of the tangent drawn from a point 8 cm away from the centre of a circle, of radius 6 cm, is :
Solution
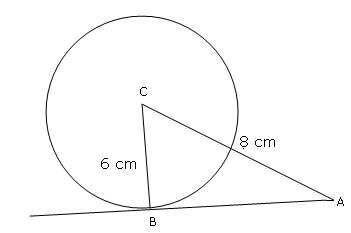 We know that the tangent to a circle is perpendicular to its radius at the point of contact.
We know that the tangent to a circle is perpendicular to its radius at the point of contact.
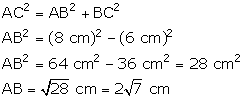 Thus, the length of the tangent is
Thus, the length of the tangent is
Q12. A circle touches all the four sides of a quadrilateral ABCD, prove that AB + CD = AD + BC 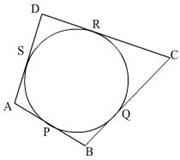

Solution
Lengths of the tangents from an external point are equal.
 AP = AS, BP = BQ, CR = CQ and DR = DS
AB + CD = (AP + BP) + (CR + DR)
= AS + BQ + CQ + DS
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence AB + CD = AD + BC.
AP = AS, BP = BQ, CR = CQ and DR = DS
AB + CD = (AP + BP) + (CR + DR)
= AS + BQ + CQ + DS
= (AS + DS) + (BQ + CQ)
= AD + BC
Hence AB + CD = AD + BC.
Q13. A tangent is a
Solution
A tangent is a line which intersects exactly at one point.
Q14. From the given figure, ∠TPQ and ∠TOQ are
Solution
∠TPQ and ∠TOQ are complementary angles as ∠OTP =∠OQP = 90°.
Q15. The number of tangents which can be drawn to a circle from a point
lying within is
Solution
The number of tangents which can be drawn to a circle from a point
lying within is zero.
Q16. ____ drawn from the external point to a circle are equal in
length.
Solution
Tangents drawn from the external point to a circle are equal in
length.
Q17. If PQ = 4 cm and OQ = 5 cm, then find the radius of the tangent.
Solution
OP2 + PQ2 = OQ2
OP2 + 42 = 52
OP2 = 9
OP = r = 3 cm
Q18. Number of tangents from a point lying inside the circle is
Solution
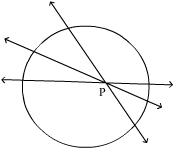 All the lines through a point inside a circle intersect the circle in two points. So, it is not possible to draw any tangent to a circle through a point inside it.
All the lines through a point inside a circle intersect the circle in two points. So, it is not possible to draw any tangent to a circle through a point inside it.
Q19. O is the centre of the circle. ST and SR are tangents segments. Show that the quadrilateral STOR is cyclic. 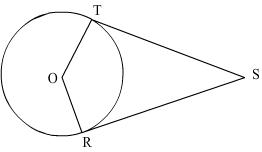

Solution
OT TS and OR
TS and OR 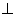 RS (Tangent at a point to a circle
RS (Tangent at a point to a circle 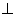 to the radius at that point)
to the radius at that point)
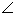 OTS = 90o and
OTS = 90o and 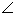 ORS = 90o
ORS = 90o
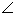 OTS +
OTS +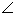 ORS= 180o
In quadrilateral STOR,
ORS= 180o
In quadrilateral STOR,
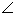 OTS +
OTS +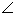 ORS +
ORS + 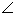 TOR +
TOR + 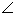 TSR = 360o
(
TSR = 360o
(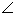 OTS +
OTS +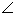 ORS)+ (
ORS)+ (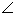 TOR +
TOR + 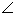 TSR) = 360o
(
TSR) = 360o
(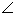 TOR +
TOR + 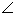 TSR) + 180o = 360o
TSR) + 180o = 360o
 TOR +
TOR + 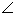 TSR = 180o
Opposite angles of the quadrilateral STOR are supplementary, hence it is cyclic.
TSR = 180o
Opposite angles of the quadrilateral STOR are supplementary, hence it is cyclic.
 TS and OR
TS and OR
Q20. In the given fig., angle OBC = 30o, then value of x is:


Solution
Q21. In fig., two circles with centres A and B touch each other externally at k. The length of PQ (in cm) is
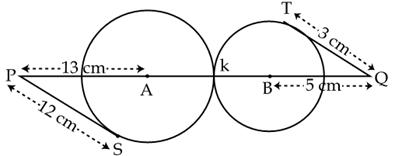

Solution
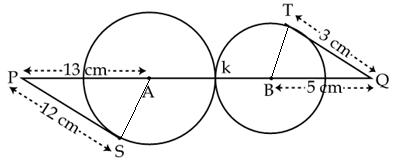 Join points B and T, A and S.
We know that radius is perpendicular to the tangent at the point of contact.
Join points B and T, A and S.
We know that radius is perpendicular to the tangent at the point of contact.
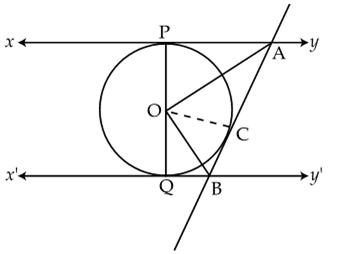
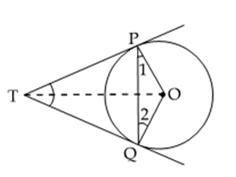
Q22. In the figure, if from an external point T, TP and TQ are two tangents to a circle with centre O so that  POQ = 110o, then,
POQ = 110o, then,  PTQ is:
PTQ is:
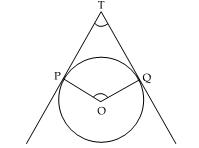

Solution
TP and TQ are tangents to the circle from a point T outside the circle.
The radius drawn to these tangents will be perpendicular to the tangents.
Thus, OP  TP and OQ
TP and OQ 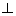 TQ
TQ
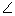 OPT = 90°and
OPT = 90°and 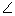 OQT = 90°
In quadrilateral POQT,
OQT = 90°
In quadrilateral POQT, 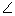 OPT +
OPT + 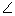 POQ +
POQ + 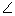 OQT +
OQT + 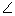 PTQ = 360°
( Sum of all interior angles of a quadrilateral = 360°)
90°+ 110° + 90° +
PTQ = 360°
( Sum of all interior angles of a quadrilateral = 360°)
90°+ 110° + 90° + 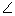 PTQ = 360
PTQ = 360
 PTQ = 70°
PTQ = 70°
Q23.  If ∠OMN = 20°, then find ∠MON.
If ∠OMN = 20°, then find ∠MON.
 If ∠OMN = 20°, then find ∠MON.
If ∠OMN = 20°, then find ∠MON. Solution
In ∆MON,
MO = ON
∠ONM = ∠NMO = 20°… (angles opposite to equal sides in a triangle)
∠MON + ∠ONM + ∠NMO = 180°… (sum of angles of a triangle)
∠MON + 40° = 180°
∠MON = 140°
Q24. The angle between two tangents drawn from an external point to a circle is 110o. The angle subtended at the centre by the segments joining the points of contact to the centre of circle is:
Solution
 TP and TQ are tangents to the circle from a point T outside the circle.
The radius drawn to these tangents will be perpendicular to the tangents.
Thus, OP
TP and TQ are tangents to the circle from a point T outside the circle.
The radius drawn to these tangents will be perpendicular to the tangents.
Thus, OP 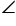 OPT = 90o and
OPT = 90o and 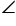 OQT = 90o
In quadrilateral POQT,
OQT = 90o
In quadrilateral POQT,
Q25. A circle is inscribed in triangle ABC. If the tangents of a triangle are 4, 5, 7, respectively, then find the perimeter of the triangle.
Solution
Consider, sides of the triangle are x, y and z.
x + y + z = 2 × 4 + 2 × 5 + 2 × 7
Tangents drawn from external points to a circle are equal.
x + y + z = 8 + 10 + 14 = 32
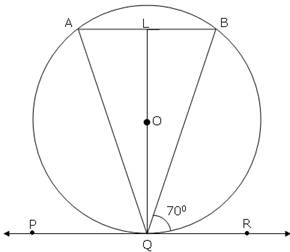
Q26. In fig., APB is a tangent to a circle with centre O, at point P. 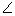 QPB = 50o, then the measure of
QPB = 50o, then the measure of 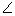 POQ is:
POQ is:
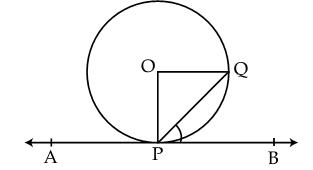

Solution
We know that the radius is perpendicular to the tangent at the point of contact.
So,  OPB = 90o
OPB = 90o

 OPQ =
OPQ =  OPB -
OPB - 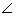 QPB = 90o - 50o = 40o
In
QPB = 90o - 50o = 40o
In  OPQ,
OPQ,
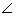 OPQ =
OPQ = 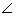 OQP (OQ = OP, radii of same circle. And, in a triangle, angles opposite to equal sides are equal)
Using angle sum property,
OQP (OQ = OP, radii of same circle. And, in a triangle, angles opposite to equal sides are equal)
Using angle sum property,
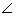 OPQ +
OPQ + 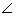 OQP +
OQP + 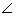 POQ = 180o
40o + 40o +
POQ = 180o
40o + 40o + 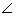 POQ = 180o
POQ = 180o
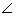 POQ = 100o
POQ = 100o
Q27. In figure,
l and m are two parallel tangents
at A and B. The tangent at C makes an intercept DE between l and m. Prove that DE subtends a
right angle at the centre O of the circle.


Solution
Join
OC.
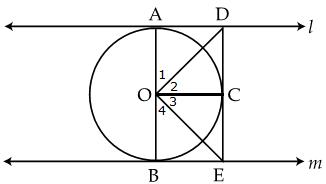 In
In
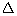 DAO and
DAO and 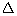 DCO,
OA
= OC = r
DCO,
OA
= OC = r
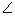 OAD
=
OAD
= 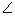 OCD = 90o
(Radius
is perpendicular to tangent at the point of contact)
OD
= OD (common)
OCD = 90o
(Radius
is perpendicular to tangent at the point of contact)
OD
= OD (common)
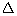 DAO
DAO
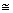
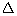 DCO (RHS
congruency criterion)
We
know corresponding parts of congruent triangles are equal.
DCO (RHS
congruency criterion)
We
know corresponding parts of congruent triangles are equal.

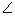 1
=
1
=  2 ...
(i)
Similarly
2 ...
(i)
Similarly  OBE
OBE 
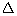 OCE
Then,
OCE
Then,
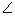 3 =
3 = 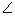 4 ... (ii)
As
AOB is a line,
4 ... (ii)
As
AOB is a line, 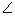 1 +
1 + 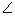 2 +
2 + 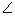 3 +
3 + 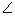 4 = 180o
2
4 = 180o
2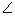 2 + 2
2 + 2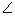 3 = 180o
3 = 180o
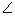 2
+
2
+ 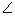 3 = 90o, i.e.,
3 = 90o, i.e., 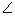 DOE = 90o
DOE = 90o
 In
In
Q28. In fig., PQR is the tangent to a circle at Q whose centre is O. AB is a chord parallel to PR and angle BQR = 70o, then angle AQB is equal to

Solution
Since AB || PR and OQ  PR (Radius is perpendicular to tangent), OL
PR (Radius is perpendicular to tangent), OL  AB.
AB.
 OL bisects chord AB.
Thus,
OL bisects chord AB.
Thus,  QAB is isosceles.
QAB is isosceles.

 LQB =
LQB = 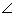 LQA
But
LQA
But 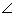 LQB = 90o - 70o = 20o
LQB = 90o - 70o = 20o

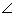 LQA = 20o
LQA = 20o
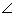 AQB = 2
AQB = 2 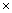 (20o) = 40o
(20o) = 40o
Q29. Find the semi-perimeter of a triangle.

Solution
PC = PA = 6 cm, QA = QB = 5 cm, RC = RB = 7 cmSemi-perimeter of a triangle =  = 18 cm
= 18 cm
 = 18 cm
= 18 cm
Q30. In fig., if PT is a tangent of the circle with centre O and 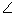 TPO = 25o, then the measure of x is :
TPO = 25o, then the measure of x is :
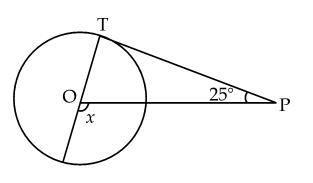

Solution
We know that the radius is perpendicular to the tangent at the point of contact.
So,  OTP = 90o
We also know that the measure of an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
x =
OTP = 90o
We also know that the measure of an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
x =  OTP +
OTP +  TPO = 90o + 25o = 115o
TPO = 90o + 25o = 115o
Q31. If two parallel lines are intersected by a transversal such
that the pair of ______ is not equal.
Solution
If two parallel lines are intersected by a
transversal such that the pair of interior angle is not equal.
Q32. In fig., PA is a tangent to a circle of radius 6 cm and PA = 8 cm, then length of PB is
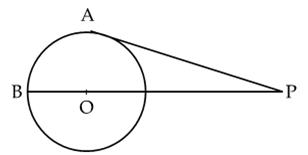

Solution
PB=PO+OB
If we join OA,
 PO2= PA2+OA2
= 64 + 36 = 100
PO = 10 cm
PB = 10+6
= 16 cm
PO2= PA2+OA2
= 64 + 36 = 100
PO = 10 cm
PB = 10+6
= 16 cm
Q33. In the
figure, O is the centre of a circle and BCD is tangent to it at C. Prove that
 BAC +
BAC +  ACD = 90o.
ACD = 90o.


Solution
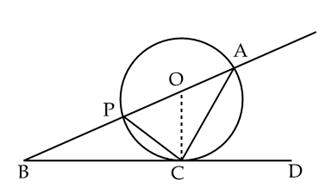 OA
= OC (radii of same circle)
OA
= OC (radii of same circle)
Q34. In
fig., triangle ABC is a right angled triangle with AB = 6 cm, AC = 8 cm and 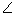 A = 90o. A circle with centre O is
inscribed inside the triangle. Find the radius 'r'.
A = 90o. A circle with centre O is
inscribed inside the triangle. Find the radius 'r'.

Solution
Q35. In fig., if OC = 9 cm and OB = 15 cm, then BC + BD is equal to:

Solution
We know that the radius is perpendicular to the tangent at the point of contact.
So,  OCB = 90o
Using Pythagoras theorem in
OCB = 90o
Using Pythagoras theorem in  OCB,
BC2 = (15)2 - (9)2 = 225 - 81 = 144
BC = 12 cm
We also know that the lengths of tangents drawn from an external point are equal. So, BC = BD
OCB,
BC2 = (15)2 - (9)2 = 225 - 81 = 144
BC = 12 cm
We also know that the lengths of tangents drawn from an external point are equal. So, BC = BD
 BC + BD = 2 BC = 2
BC + BD = 2 BC = 2  12 cm = 24 cm
12 cm = 24 cm
Q36. The number of tangents which can be drawn to a circle from a point
lying outside it is
Solution
The
number of tangents which can be drawn to a circle from a point
lying outside it is two.
Q37. A secant intersects a circle at _ points.
Solution
A secant
intersects a
circle at 2 points.
Q38. TA is a tangent to the circle, centre O, at A. OA = 20 cm, TA = 21 cm. and  OTA = 44o Find OT and
OTA = 44o Find OT and  x
x 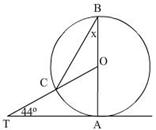

Solution
OA is the radius and TA is the tangent. 
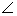 OAT = 90o
In right triangle, OAT
OT2 = OA2 + AT2
OAT = 90o
In right triangle, OAT
OT2 = OA2 + AT2  202 + 212 = 841 Hence OT = 29 cm.
In triangle OAT,
202 + 212 = 841 Hence OT = 29 cm.
In triangle OAT, 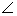 AOT = 180o – (44o + 90o) (By angle sum)
= 46o
AOT = 180o – (44o + 90o) (By angle sum)
= 46o
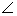 COB = 180o – 46o = 134o
In triangle COB, CO = OB
COB = 180o – 46o = 134o
In triangle COB, CO = OB
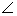 x +
x + 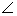 x + 134o = 180o (By angle sum)
x + 134o = 180o (By angle sum)
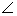 x =
x =  = 23o
OT = 29 cm and
= 23o
OT = 29 cm and 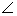 x = 23o.
x = 23o.
 = 23o
OT = 29 cm and
= 23o
OT = 29 cm and
Q39. Three circles with centres at P, Q and R touch each other externally
such that PQ = 6 cm, PR = 8 cm and QR = 12 cm. Find the greatest radius.
Solution
Let a, b and c be the radii of the circles, respectively.
a + b = 6, b + c = 8 and a + c = 12 … (i)
2(a + b + c) = 6 + 8 + 12
a + b + c = 13 … (ii)
Solving (i) and (ii),
We get a = 5, b = 1 and c = 7
The
greatest radius is (a + c) = 7 cm.
Q40. In the
figure, xy and x'y' are two parallel tangents to a circle with centre O and
another tangent AB, with point of contact C intersects xy at A and x'y' at B.
Prove that 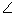 AOB = 90o.
AOB = 90o.

Solution
 OP
OP
Q41. ∠POQ = 65°, then find ∠TPO.

Solution
∠POQ = ∠POT = 65°∠TOQ = ∠POQ +∠POT
∠TOQ = 130°
∠TPQ and ∠TOQ are supplementary.
∠TPQ = 180° − 130°
∠TPQ = 50°
 ×∠TPQ = 25°
∠TPO = ∠QPO = 25°
×∠TPQ = 25°
∠TPO = ∠QPO = 25°
 ×∠TPQ = 25°
∠TPO = ∠QPO = 25°
×∠TPQ = 25°
∠TPO = ∠QPO = 25°
Q42. OA = 17 cm and AB = 8 cm. Find OB.

Solution
In ∆OBA,
OA2 = OB2 + AB2
172 = OB2 + 82
OB2 = 225
OB = 15 cm
OB2 = 225 - 64
OB2 = 225
OB = 15 cm
Q43. The length of tangent drawn from an external point P to a circle, with centre O, is 8 cm. If the radius of the circle is 6 cm, then the length of OP (in cm) is:
Solution
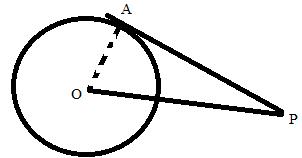 Given, AP = 8 cm and OA = 6 cm
We know that radius is perpendicular to the tangent at the point of contact.
Given, AP = 8 cm and OA = 6 cm
We know that radius is perpendicular to the tangent at the point of contact.
Q44. By which of the following properties is ∆OPR congruent to ∆OQR?

Solution
By the SSS property of congruence, ∆OQR.
Q45. A circle can have ____ number of tangent/s.
Solution
A circle can have infinite number of tangents.
Q46. The maximum number of common tangents that can be drawn to two circles intersecting at two distinct point is
Solution
There can be maximum 2 such tangents.


Q47. In the
figure, OP is equal to the diameter of the circle. Prove that ABP is an
equilateral triangle.


Solution
Say,Radius
(OA) = r
 OP = 2r………given,OP= diameter of the circle
OP = 2r………given,OP= diameter of the circle
 OAP = 90o (Tangent is
OAP = 90o (Tangent is  to the radius
through the point of contact)
In
right
to the radius
through the point of contact)
In
right  OAP
sin
(
OAP
sin
(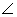 OPA) =
OPA) = 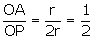
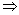
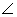 OPA = 30o
Similarly
OPA = 30o
Similarly
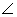 OPB = 30o
OPB = 30o

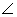 APB = 30o + 30o = 60o
Since
PA = PB (Lengths of tangents from an external point are equal)
APB = 30o + 30o = 60o
Since
PA = PB (Lengths of tangents from an external point are equal)
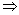
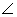 PAB =
PAB = 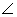 PBA
In
PBA
In
 APB,
APB,
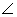 APB
+
APB
+ 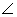 PAB +
PAB + 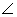 PBA = 180o (angle sum property)
PBA = 180o (angle sum property)
 60o + 2
60o + 2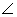 PAB = 180o
PAB = 180o
 PAB = 60o
PAB = 60o

 PBA = 60o
Since
all angles are 60o,
PBA = 60o
Since
all angles are 60o,  ABP is equilateral triangle.
ABP is equilateral triangle.
Q48. 

Solution
Q49. Prove
that the tangents drawn at the end points of a chord of a circle make equal
angles with the chord.
Solution
 Let NM be a chord of a circle with
centre C.
Let tangents at M and N meet at
the point O.
Since OM is a tangent, OM
Let NM be a chord of a circle with
centre C.
Let tangents at M and N meet at
the point O.
Since OM is a tangent, OM
Q50. A circle is inscribed in triangle ABC. If the tangents of a triangle are 4, 5, 7, respectively, then find the perimeter of the triangle.
Solution
Consider, sides of the triangle are x, y
and z.
x + y + z = 2 × 4 + 2 × 5 + 2 × 7
Tangents drawn from external points to a circle are equal.
x + y + z = 8 + 10 + 14 = 32
Q51. A tangent PA is drawn from an external point P to a circle of radius 3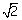 cm such that the distance of the point P from O is 6 cm as shown figure. The value of
cm such that the distance of the point P from O is 6 cm as shown figure. The value of 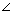 APO is
APO is
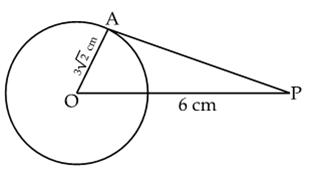

Solution
Q52. Prove
that tangent at any point of a circle is perpendicular to the radius through
the point of contact.
Solution
Given: A circle C (O, r) and a tangent AB at
a point P.
To Prove: OP is perpendicular to AB.
Construction: Take any point Q, other than P,
on the tangent AB. Join OQ.
 Since, Q is a point on the tangent AB, other
than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Then, OQ=OR+RQ
Since, Q is a point on the tangent AB, other
than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Then, OQ=OR+RQ
 OQ>OR
OQ>OR
 OQ>OP
(OR=OP=radius)
Thus, OP<OQ, i.e., OP is shorter than any
other segment joining O to any point of AB.
But, among all the line segments, joining the
point O to a point on AB, the shortest one is the perpendicular from O on AB.
Hence,
OP is perpendicular to AB.
OQ>OP
(OR=OP=radius)
Thus, OP<OQ, i.e., OP is shorter than any
other segment joining O to any point of AB.
But, among all the line segments, joining the
point O to a point on AB, the shortest one is the perpendicular from O on AB.
Hence,
OP is perpendicular to AB.
 Since, Q is a point on the tangent AB, other
than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Then, OQ=OR+RQ
Since, Q is a point on the tangent AB, other
than the point of contact P, so Q will be outside the circle.
Let OQ intersect the circle at R.
Then, OQ=OR+RQ
Q53. From the figure, ∠P + ∠O is

Solution
∠OTP = ∠OQP = 90°… (tangent ⊥ radius)
Hence, ∠P + ∠O = 180°
Q54. From a point Q, the length of the tangent to a circle is 13 cm
and the
distance of Q from the centre
is 12 cm. So,
the radius of the circle is
Solution
Using the Pythagoras theorem,
√(132
- 122) = √(169 - 144) = √25
Radius = 5 cm
Q55. By which of the following properties are triangles ∆OPB and ∆OPA congruent?

Solution
In ∆OPB and ∆OPA, OB = OA radii AP = PB OP is perpendicular bisector of AB OP = OP common∆OPB and ∆OPA are congruent by the SSS test.
? ∆OPB and ∆OPA are congruent by the SAS test.
OP = OP
∵ common side PB = PA
∵ Radius-tangent property∠OPB =∠OPA OP perpendicular to AB∆OPB ≅∆OPA
∵ SAS Also, OP = OP
∵ common side OA = OB
∵ radii of the same circle∆OPB ≅∆OPA Hypotenuse-side property
Q56. 

Solution

Q57. In fig., AP = 2 cm, BQ = 3 cm and RC = 4 cm, then the perimeter of  ABC (in cm) is
ABC (in cm) is

Solution
We know that the lengths of tangents drawn from an external point to the circle are the same.
Therefore,
AR = AP = 2 cm
BP = BQ = 3 cm
CQ = CR = 4 cm
Perimeter of  ABC = AB + BC + CA
= (AP + PB) + (BQ + CQ) + (AR + CR)
= (2 + 3 + 3 + 4 + 4 + 2) cm
= 18 cm
ABC = AB + BC + CA
= (AP + PB) + (BQ + CQ) + (AR + CR)
= (2 + 3 + 3 + 4 + 4 + 2) cm
= 18 cm
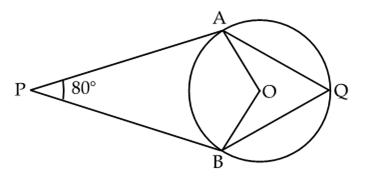
Q58. In the given figure, O is the centre of the circle. If PA and PB are tangents from an external point P to the circle, then  AQB is equal to
AQB is equal to
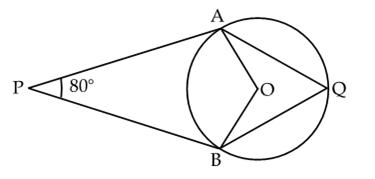

Solution
Q59. In fig., triangle ABC is circumscribing a circle. Then the length of BC is:
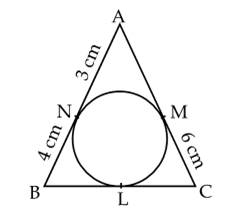

Solution
We know that the lengths of tangents drawn from an external point are equal.
 BL = BN = 4 cm and CL = CM = 6 cm
BC = BL + LC = 4 cm + 6 cm = 10 cm
BL = BN = 4 cm and CL = CM = 6 cm
BC = BL + LC = 4 cm + 6 cm = 10 cm
Q60. The radius of a circle is ____ to the tangent.
Solution
The radius of a circle is perpendicular to the tangent.
Q61. Which
of the following is correct?
Solution
A,B and C are correct.
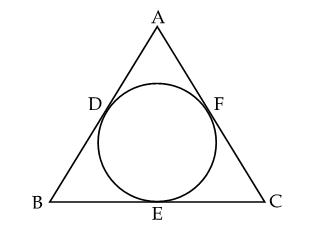
Q62. In the following fig., triangle ABC is isosceles in which AB = AC, circumscribed about a circle. Prove that base is bisected by the point of contact.

Solution
Given: AB = AC
To prove: BE = CE
Proof:
We know that the lengths of the tangents drawn from an external point to the circle are equal.
Therefore,
AD = AF,
BD = BE
CE = CF
We have: AB = AC (given)
 AB - AD = AC - AD
AB - AD = AC - AD
 AB - AD = AC - AF
AB - AD = AC - AF
 BD = CF
BD = CF
 BE = EC (Since, BD = BE and CE = CF)
BE = EC (Since, BD = BE and CE = CF)
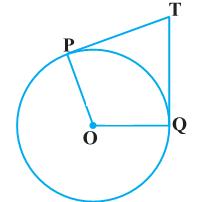
Q63. In the figure, the pair of tangents AP and AQ, drawn from an external point A to a circle with centre O, are perpendicular to each other and length of each tangent is 4 cm, then the radius of the circle is
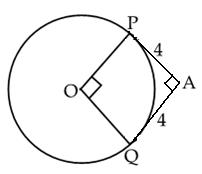

Solution
We know that radius is perpendicular to tangent at the point of contact.

 OPA=
OPA=  OQA = 90o
Clearly, it can be observed that OPAQ is a square.
All the sides of a square are equal.
OQA = 90o
Clearly, it can be observed that OPAQ is a square.
All the sides of a square are equal.
 Radius of the circle = OP = PA = 4 cm
Radius of the circle = OP = PA = 4 cm
Q64. If two parallel tangents PQ and RS touch the circle C at
A and B, respectively, then AB is the ___ of the circle.
Solution
Two parallel tangents PQ and RS touch the circle C at
A and B, respectively, then AB is the diameter of the circle.
Q65. Prove
that the lengths of tangents drawn from an external point to a circle are
equal.
Solution
Consider
a circle with centre O. Let PT and PQ be the two tangents drawn from the
point P to the circle.
We
have to prove that PT = PQ.
Join OP, OT and OQ.
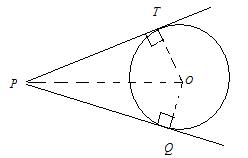 In
ΔOTP and ΔOQP,
OT = OQ (Radii
of the same circle)
In
ΔOTP and ΔOQP,
OT = OQ (Radii
of the same circle)
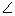 OTP =
OTP = 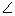 OQP = 90°
(The
tangent is perpendicular to the radius through the point of contact)
OP
= OP (Common)
OQP = 90°
(The
tangent is perpendicular to the radius through the point of contact)
OP
= OP (Common)
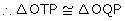 (By R.H.S.
congruence criterion)
Since,
corresponding parts of congruent triangles are equal, PT = PQ.
Hence,
proved.
(By R.H.S.
congruence criterion)
Since,
corresponding parts of congruent triangles are equal, PT = PQ.
Hence,
proved.
 In
ΔOTP and ΔOQP,
OT = OQ (Radii
of the same circle)
In
ΔOTP and ΔOQP,
OT = OQ (Radii
of the same circle)
Q66. In the figure if 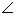 ATB = 40o, find
ATB = 40o, find  AOB.
AOB. 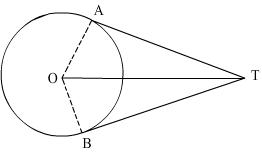

Solution
Here quadrilateral AOBT is a cyclic quadrilateral and OA AT and OB
AT and OB BT.
BT.
 OAT =
OAT =  OBT = 90o
OBT = 90o

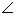 ATB +
ATB + 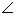 AOB = 180o
Also given is
AOB = 180o
Also given is 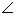 ATB = 40o
ATB = 40o

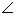 AOB.= 140o
AOB.= 140o
 AT and OB
AT and OB BT.
BT.

Q67. In two concentric circles, prove that all chords of the outer circle that touch the inner circle are of equal length
Solution
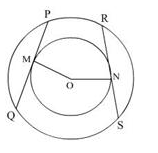 Let PQ and RS be the chords of the circle that touch the inner circle at M and N respectively.
PQ and RS are the tangents to the inner circle, and OM and ON are the radii of the smaller circle.
Let PQ and RS be the chords of the circle that touch the inner circle at M and N respectively.
PQ and RS are the tangents to the inner circle, and OM and ON are the radii of the smaller circle.
Q68. In the following fig., from an external point P, PA and PB are tangents to the circle with centre O. If CD is another tangent at point E to the circle and PA = 12 cm. Find the perimeter of  PCD.
PCD.
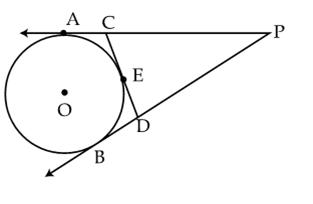

Solution
Tangents drawn from an external point to the circle are equal.
 PA = PB = 12 cm
Also,
PA = PB = 12 cm
Also, 
 Perimeter of
Perimeter of  PCD = PC + CD + PD
= PC + CE + ED + PD
= PC + AC + BD + PD
= PA + PB = 24 cm
PCD = PC + CD + PD
= PC + CE + ED + PD
= PC + AC + BD + PD
= PA + PB = 24 cm
Q69. Two concentric circles have centre at O, OP = 4 cm and OB = 5 cm. AB is a chord of the other circle and a tangent to the inner circle at P. Find the length of AB.
Solution
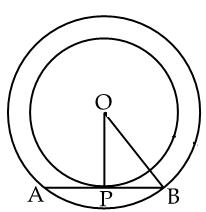 OP = 4 cm, OB = 5 cm
We know that the radius is perpendicular to the tangent at the point of contact.
OP = 4 cm, OB = 5 cm
We know that the radius is perpendicular to the tangent at the point of contact.
Q70. In two concentric circles the radius of inner is 5 cm a chord of length 24 m of outer circle becomes a tangent to the inner circle. Find the radius of the larger circle.
Solution
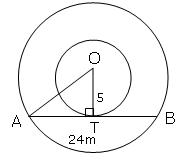 Let O be the centre of circle and AB be the chord OT is radius of smaller circle
So OT
Let O be the centre of circle and AB be the chord OT is radius of smaller circle
So OT
Q71. Prove
that tangents drawn at the end-points of a diameter of a circle are parallel.
Solution
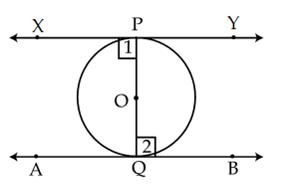 To
prove: XY || AB
We
know that radius is perpendicular to the tangent at the point of contact.
To
prove: XY || AB
We
know that radius is perpendicular to the tangent at the point of contact.
Q72. Quadrilateral ABCD circumscribes a circle as shown in figure. The side of the quadrilateral which is equal to AP + BR is:
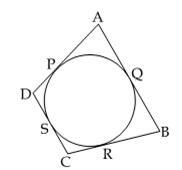

Solution
In the quadrilateral ABCD:
AP + BR
= AQ + BQ
(AQ = AP and BQ = BR…lengths of tangents drawn from an external point to a circle are equal.)
=AB
Q73. 

Solution
Q74. Two
tangents TP and TQ are drawn to a circle with centre O from an external point
T. Prove that  PTQ = 2
PTQ = 2 OPQ.
OPQ.
Solution
 We
know that tangent to a circle is perpendicular to its radius at the point of
contact.
So,
We
know that tangent to a circle is perpendicular to its radius at the point of
contact.
So,
Q75. In the diagram, the circle touches AB produced at P, AC produced at R and BC produced at Q. AB = 23 cm, BC = 17 cm. and AC = 20 cm. Find the lengths Of AP and CQ 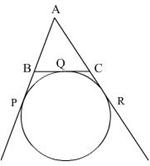

Solution
Tangents from an external point are equal.
 AP = AR, BP = BQ, CQ = CR
BP = BQ = BC – CQ or BC – CR or 17 – CR. Hence BP = 17 – CR.
Now AP = AR
Or AB + BP = AC + CR
Or 23 + 17 – CR = 20 + CR
Or 2 CR = 40 – 20
AP = AR, BP = BQ, CQ = CR
BP = BQ = BC – CQ or BC – CR or 17 – CR. Hence BP = 17 – CR.
Now AP = AR
Or AB + BP = AC + CR
Or 23 + 17 – CR = 20 + CR
Or 2 CR = 40 – 20
 CR = 10 cm.
Now BP = 17 – 10 = 7 cm, and AP = AB + BP
CR = 10 cm.
Now BP = 17 – 10 = 7 cm, and AP = AB + BP  23 + 7 = 30 cm.
Hence AP = 30 cm and CR = CQ = 10 cm.
23 + 7 = 30 cm.
Hence AP = 30 cm and CR = CQ = 10 cm.
Q76. Which of the following is incorrect?
Solution
RC and PB are not drawn from a common external
point.
Q77. ____ drawn from the external point to a circle are equal in
length.
Solution
Tangents
drawn from the
external point to a circle are equal in
length.
Q78. Prove
that the parallelogram circumscribing a circle is a rhombus.
Solution
Since
ABCD is a parallelogram,
AB
= CD (i)
BC
= AD (ii)
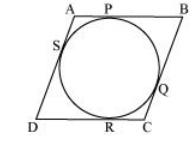 Now,
we may observe that
DR
= DS (tangents on circle
from point D)
CR
= CQ (tangents on circle
from point C)
BP
= BQ (tangents on circle
from point B)
AP
= AS (tangents on circle
from point A)
Adding
all these equations, we get,
DR
+ CR + BP + AP = DS + CQ + BQ + AS
(DR
+ CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD
+ AB = AD + BC
From
equation (i) and (ii), we get,
2AB
= 2BC
AB
= BC
Or,
AB = BC = CD = DA
Hence,
ABCD is a rhombus.
Now,
we may observe that
DR
= DS (tangents on circle
from point D)
CR
= CQ (tangents on circle
from point C)
BP
= BQ (tangents on circle
from point B)
AP
= AS (tangents on circle
from point A)
Adding
all these equations, we get,
DR
+ CR + BP + AP = DS + CQ + BQ + AS
(DR
+ CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD
+ AB = AD + BC
From
equation (i) and (ii), we get,
2AB
= 2BC
AB
= BC
Or,
AB = BC = CD = DA
Hence,
ABCD is a rhombus.
 Now,
we may observe that
DR
= DS (tangents on circle
from point D)
CR
= CQ (tangents on circle
from point C)
BP
= BQ (tangents on circle
from point B)
AP
= AS (tangents on circle
from point A)
Adding
all these equations, we get,
DR
+ CR + BP + AP = DS + CQ + BQ + AS
(DR
+ CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD
+ AB = AD + BC
From
equation (i) and (ii), we get,
2AB
= 2BC
AB
= BC
Or,
AB = BC = CD = DA
Hence,
ABCD is a rhombus.
Now,
we may observe that
DR
= DS (tangents on circle
from point D)
CR
= CQ (tangents on circle
from point C)
BP
= BQ (tangents on circle
from point B)
AP
= AS (tangents on circle
from point A)
Adding
all these equations, we get,
DR
+ CR + BP + AP = DS + CQ + BQ + AS
(DR
+ CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD
+ AB = AD + BC
From
equation (i) and (ii), we get,
2AB
= 2BC
AB
= BC
Or,
AB = BC = CD = DA
Hence,
ABCD is a rhombus.
Q79. 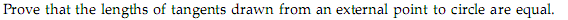
Solution
Q80. Two concentric circles have centre O. A
chord PQ of the larger circle is bisected by the smaller circle at point R, so PQ is ____ to the smaller circle.
Solution
Two concentric circles have centre O. A
chord PQ of the larger circle is bisected by the smaller circle at point R, so PQ is tangent to the smaller circle.
Q81. Which of the following is correct from the following
figure?

Solution
From the figure,
A, B and C are correct.
Q82. In the following fig., triangle ABC is a right angled triangle with AB = 6 cm, AC = 8 cm and  A = 90o. A circle with centre O is inscribed inside the triangle. Find the radius 'r'.
A = 90o. A circle with centre O is inscribed inside the triangle. Find the radius 'r'.

Solution

Q83. In fig., ABC is a triangle right angled at
A. Find the area of the shaded region if AB = 6 cm, BC = 10 cm and L is the
centre of incircle of  ABC.
ABC.
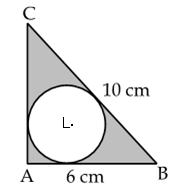

Solution
Given,
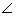 A = 90o, AB = 6 cm and BC = 10 cm
A = 90o, AB = 6 cm and BC = 10 cm
 Area
of
Area
of  ABC =
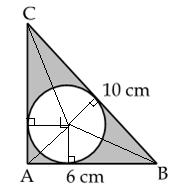
ABC = 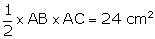 Let
r be the radius of incircle. Join LA, LB and LC.
We
know that radius is perpendicular to the tangent at the point of contact.
Let
r be the radius of incircle. Join LA, LB and LC.
We
know that radius is perpendicular to the tangent at the point of contact.
 Therefore,
Area
of
Therefore,
Area
of  ABC = Area of
ABC = Area of  ALB + Area of
ALB + Area of  BLC + Area of
BLC + Area of  ALC
ALC
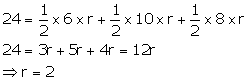 Thus,
the radius of the incircle is 2 cm.
Area
of shaded region = area of triangle ABC - area of circle
Thus,
the radius of the incircle is 2 cm.
Area
of shaded region = area of triangle ABC - area of circle
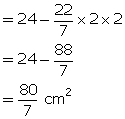
 Therefore,
Area
of
Therefore,
Area
of 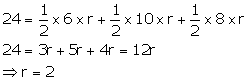 Thus,
the radius of the incircle is 2 cm.
Area
of shaded region = area of triangle ABC - area of circle
Thus,
the radius of the incircle is 2 cm.
Area
of shaded region = area of triangle ABC - area of circle
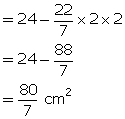
Q84. In the given figure, the diameter AB of the circle with centre O is extended to a point P and PQ is a tangent to the circle at the point T. If 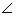 BPT = x and
BPT = x and 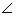 ATP = y, then prove that x + 2y = 90o.
ATP = y, then prove that x + 2y = 90o.


Solution
Join OT.
 It is known that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
It is known that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

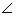 OTP = 90o
In a triangle, the measure of an exterior angle is equal to the sum of the measures of its interior opposite angles.
Therefore, in
OTP = 90o
In a triangle, the measure of an exterior angle is equal to the sum of the measures of its interior opposite angles.
Therefore, in  PAT,
PAT,
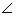 OAT =
OAT = 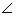 APT +
APT + 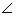 ATP
ATP

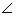 OAT = x + y
In
OAT = x + y
In  OAT, OA = OT (Radii of the same circle)
OAT, OA = OT (Radii of the same circle)

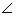 OAT =
OAT = 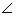 OTA
OTA
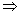 x + y =
x + y = 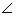 OTP -
OTP - 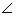 ATP
ATP
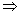 x + y = 90o - y
x + y = 90o - y
 x + 2y = 90o
x + 2y = 90o
 It is known that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
It is known that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Q85. In
fig., O is the centre of two concentric circles of radii 6 cm and 4 cm. PQ
and PR are tangents to the two circles from an external point P. If PQ = 10
cm, find the length of PR.
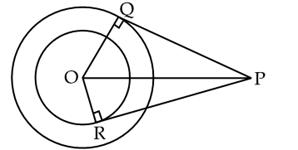

Solution
We
know that the radius is perpendicular to the tangent at the point of contact.

 PQO =
PQO =  PRO = 90o
In
PRO = 90o
In
 POQ,
Given
PQ = 10 cm, OQ = 6 cm
POQ,
Given
PQ = 10 cm, OQ = 6 cm
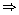 OP =
OP = 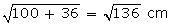 In
In
 POR,
OP2
= 42 + PR2
POR,
OP2
= 42 + PR2
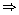 136 - 16 = PR2
136 - 16 = PR2
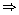 PR2 = 120
PR2 = 120
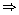 PR =
PR = 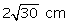
Q86. In the figure, AB and CD are two parallel tangents to a circle with centre O. ST is the tangent segment between two parallel tangents to a circle with centre O. ST is the tangent segment between two parallel tangents touching the circle at Q. Show that  SOT = 90o.
SOT = 90o.


Solution
 Join OP and OQ.
In
Join OP and OQ.
In
Q87. Prove
that the line segment joining the points of contact of two parallel tangents
to circle is a diameter of the circle.
Solution
 Construction:
Through O draw OR || BA or OR || CD as AB and CD are parallel tangents.
Proof:
Construction:
Through O draw OR || BA or OR || CD as AB and CD are parallel tangents.
Proof:
Q88. In
fig., tangent segments PS and PT are drawn to a circle with centre O such
that  SPT = 120o. Prove that OP = 2 PS.
SPT = 120o. Prove that OP = 2 PS.
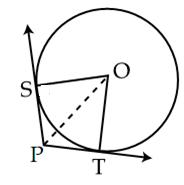

Solution
Tangents
drawn from an external point to the circle are equal.
 PS = PT
Radius is perpendicular to the tangent at the point
of contact.
PS = PT
Radius is perpendicular to the tangent at the point
of contact.
 In
In  OST and
OST and  OTP,
OTP,
 PS = PT
OS = OT (Radii
of same circle)
PS = PT
OS = OT (Radii
of same circle)
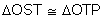

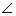 OPS
=
OPS
= 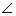 OPT
OPT
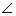 SPT
= 120o
SPT
= 120o 
 OPS = 60o
In
OPS = 60o
In
 OSP,
OSP,

 OP = 2 PS
OP = 2 PS
Q89. In
fig., a quadrilateral ABCD circumscribes a circle, Prove that AB + DC = AD +
BC.
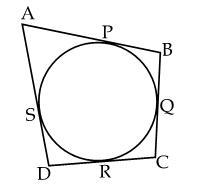

Solution
We
know that the lengths of the tangents drawn from an external point are equal.
Therefore,
we have:
AP
= AS, BP = BQ, CR = QC, DR = DS
Adding the above equations, we have:
AP
+ PB + RC + DR = AS + BQ + QC + DS
 AB + DC = AD + BC
AB + DC = AD + BC
Q90. AB and AC are tangents from A to the circle with center O. M is a point on the circle. Prove that, AP + PM = AQ + QM.
Solution
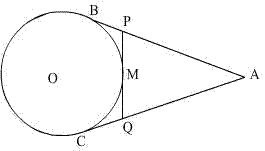 Lengths of the tangents from an external point to a circle are equal.
Lengths of the tangents from an external point to a circle are equal.
Comments
Post a Comment