Q1. State whether the following real numbers are rational or not:
(i)  (ii) 47.5369821 (iii) 3.2010010001……
(ii) 47.5369821 (iii) 3.2010010001……
Solution
(i) rational (ii) rational (iii) irrational
Q2. Find the HCF of 75 and 243 by
Euclid’s division lemma.
Solution
243
= 75 × 3 + 18
75
= 18 × 4 + 3
18
= 3 × 6 + 0
Hence,
HCF of 75 and 243 is 3.
Q3. Give an example and show that the sum of two irrational may be an irrational number but their product may not always be an irrational number.
Solution
Consider two numbers 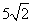 and
and 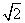 Addition=
Addition=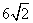 Product=10
So we see that the addition is an irrational number but the product is a rational number.
Product=10
So we see that the addition is an irrational number but the product is a rational number.
Q4. Which of the following is rational?
Solution
Since, 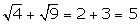 , it is rational.
, it is rational.
Q5. For any two positive integers a and b, there exist unique integers q and r such that a = bq + r, 0 ≤ r < b. If b = 4 then which is not the value of r?
Solution
Given, a = bq + r, 0 ≤ r < b and b = 4
So, r can take values 0, 1, 2, 3.
Thus, r ≠ 4.
Q6. If H.C.F. of 65 and 117 is expressible in the form of 65 m - 117, then the value of m is :
Solution
65 = 13 × 5 and 117 = 13 × 9
So, HCF (65, 117) = 13
Because HCF of 65 and 117 is 13,which is expressible in the form 65 m - 117
Thus we get 65 m - 117 = 13
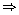 65 m = 130
65 m = 130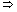 m = 2
m = 2
Q7. A rational number between 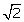 and
and 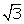 is:
is:
Solution
Q8. Find
HCF of 592 and 252 by using Euclid’s Division Algorithm.
Solution
In the given pair, 592 > 252,
thus let 592 = a and 252 = b.
Now by applying the Euclid’s
division algorithm a = bq + r, we get
592 = 252 × 2 + 88
252 = 88 × 2 + 76
88 = 76 × 1 + 12
76 = 12 × 6 + 4
12 = 4 × 3 + 0
Since
in the above equation we get r = 0; therefore, 4is the HCF of the given pair
592 and 252.
Q9. Without actually performing division state whether the number 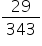 will have a terminating decimal representation or not.
will have a terminating decimal representation or not.
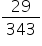 will have a terminating decimal representation or not.
will have a terminating decimal representation or not.Solution
A rational number will have a terminating decimal representation only if the denominator can be expressed in terms of prime numbers 2 and 5. We see that,
343=7 x 7 x 7So according to the condition given above, the denominator of 29/343 can not be expressed fully in terms of 2 and 5.
Hence, the number can't have a terminating decimal representation.
Q10. Given that HCF (26 , 91) = 13, then LCM of (26 , 91) is :
Solution
HCF(26, 91) = 13 and let the LCM(26, 91) = x
We know LCM  HCF = 26
HCF = 26  91
91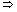 13
13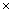 x = 26
x = 26 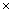 91
91
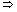 x =
x =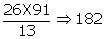
Q11. Is 7 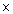 6
6 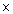 5
5 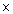 4
4 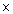 3
3 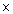 2
2 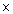 1 + 5 a composite number? Justify your answer.
1 + 5 a composite number? Justify your answer.
Solution
7 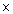 6
6 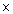 5
5 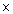 4
4 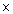 3
3 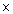 2
2 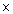 1 + 5 = 5040 + 5 = 5045
It has more than two prime factors.
Thus, the given number is a composite number.
1 + 5 = 5040 + 5 = 5045
It has more than two prime factors.
Thus, the given number is a composite number.
Q12. The value of x in the factor tree is:
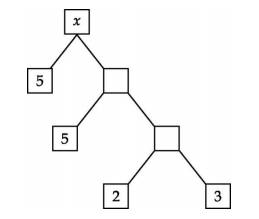

Solution
 To find the value of x, we will have to go backwards.
2 × 3 = 6
Further, 6 × 5 = 30
Then 30 × 5 = 150
Thus, x = 150
To find the value of x, we will have to go backwards.
2 × 3 = 6
Further, 6 × 5 = 30
Then 30 × 5 = 150
Thus, x = 150
Q13. The length, breadth and height of a
room is 6m 80 cm, 5m 10 cm and 3 m 40 cm, respectively. Find the longest tape
which can measure the dimensions of the room exactly.
Solution
6m
80 cm = 680 cm
5m
10 cm = 510 cm
3m
40 cm = 340 cm
We
have to find HCF of 680, 510 and 340.
HCF
of 680 and 510,
680
= 510 × 1 + 170
510
= 170 × 3 + 0
∴ HCF (680, 510) = 170
HCF
of 170 and 340,
340
= 170 × 2 + 0
∴ HCF (170, 340) = 170
∴ HCF
(680, 510, 340) = 170
170
cm = 1m 70 cm
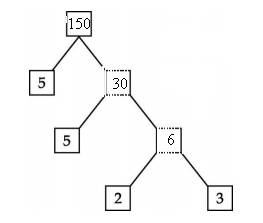
Q14. Prove that tan1° tan2° tan3°… tan89° = 1.
OR
Prove that 
Solution
tan1° tan2° tan3° … tan89°
= tan1° tan2° tan3°… tan44° tan45° tan46°… tan88° tan89°
= tan1° tan89° tan2° tan88° ………. tan 44° tan46° tan45° (½)
= tan1° tan(90° - 1°) tan2° tan(90° - 2°) … tan 44° tan(90° - 44°) tan45° (½)
= tan1° cot1° tan2° cot2° … tan 44° cot44° tan45° (½)
= 1 (½)
OR
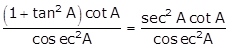 (½)
(½)
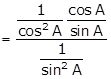 (½)
(½)

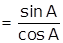 (½)
= tan A
∴
(½)
= tan A
∴ 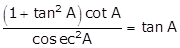 (½)
(½)
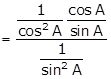 (½)
(½)
Q15. What is the probability that a leap year selected at random will have 53 Sundays?
OR
What is the probability that a number selected from the first 25 natural numbers is a prime number?
Solution
A leap year contains 366 days, i.e. 52 weeks and 2 additional days. The possibility for these two additional days are
Sample space = {(Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday)}
n(S) = 7 (1)
Thus, there are seven possibilities out of which two are favourable for getting the 53rd Sunday.
A = {(Sunday, Monday), (Saturday, Sunday)} (1)
n(A) = 2
P(A) = n(A) / n(S) = 2/7 (1)
OR
S = {1, 2, 3, 4, 5, … 25}
n(S) = 25 (1)
Let A denote the event of getting a prime number.
A = {2, 3, 5, 7, 11, 13, 17, 19, 23} (1)
n(A) = 9
P(A) = n(A)/n(S) = 9/25 (1)
Q16. Euclid’s division lemma
can be used to find
Solution
Euclid’s division lemma
can be used to find HCF of numbers.
Q17. Use Euclid's division algorithm to find the HCF of 10224 and 9648.
Solution
Here 10224> 9648
By Euclid Division Algorithm,
10224 = 9648  1 + 576
9648 = 576
1 + 576
9648 = 576  16 + 432
576 = 432
16 + 432
576 = 432  1 + 144
432 = 144
1 + 144
432 = 144  3 + 0
3 + 0
 HCF (10224, 9648) = 144
HCF (10224, 9648) = 144
Q18. Solve : 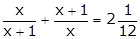
Solution

Q19. Find the H.C.F. and L.C.M. of 6, 72 and 120 using the prime factorisation method.
Solution

Q20. Prove that 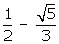 is irrational.
is irrational.
Solution
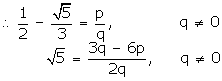
Q21. Which of the following is a non-terminating, repeating decimal?
Solution
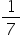 is not of the form,
is not of the form, 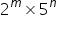 Thus,
Thus,
Q22. Prove that 13 + 25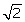 is irrational.
is irrational.
Solution
Let us assume, on contrary that 13 + 25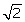 is rational.
is rational.
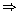 13 + 25
13 + 25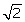 =
= 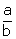 , where a and b are integers and b ≠ 0.
, where a and b are integers and b ≠ 0.
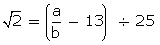
 a and b are integers,
a and b are integers, 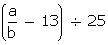 is rational.
is rational.
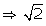 is rational.
But this contradicts the fact that
is rational.
But this contradicts the fact that 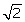 is irrational.
This contradiction has arisen because of our incorrect assumption that 13 + 25
is irrational.
This contradiction has arisen because of our incorrect assumption that 13 + 25  is rational.
Hence, 13 + 25
is rational.
Hence, 13 + 25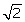 is irrational.
is irrational.
Q23. Find the ratio in which the line 2x + y - 4 = 0 divides the line segment joining a(2, −2) and B(3, 7).
OR
Find the value of k for which the area formed by the triangle with vertices A(k, 2k), B(−2, 6) and C(3, 1) is 5 square units.
Solution
Let the required ratio be k:1.
Let P(x, y) be the point on the given line dividing AB in the ratio k:1. Then
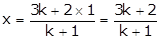 and
and 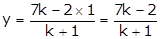 (1)
This point P(x, y) lies on the line 2x + y - 4 = 0.
(1)
This point P(x, y) lies on the line 2x + y - 4 = 0.
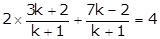 (1)
6k + 4 + 7k - 2 = 4k + 4
9k = 2
k = 2/9 (1)
Hence, the required ratio is 2:9. (1)
OR
Vertices of the given triangle ABC are A(k, 2k), B(−2, 6) and C(3, 1).
x1 = k, y1 = 2k, x2 = −2, y2 = 6 and x3 = 3, y3 = 1
Area of triangle ABC
=
(1)
6k + 4 + 7k - 2 = 4k + 4
9k = 2
k = 2/9 (1)
Hence, the required ratio is 2:9. (1)
OR
Vertices of the given triangle ABC are A(k, 2k), B(−2, 6) and C(3, 1).
x1 = k, y1 = 2k, x2 = −2, y2 = 6 and x3 = 3, y3 = 1
Area of triangle ABC
=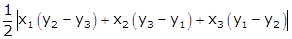 =
= 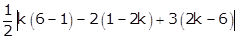 =
= 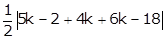 =
= 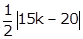 (2)
According to the question,
(2)
According to the question,
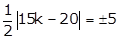
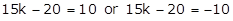
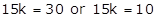
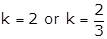 (2)
(2)
Q24. Given that HCF (2520, 6600) = 120, LCM (2520, 6600) = 252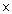 k, then the value of k is:
k, then the value of k is:
Solution
We know that the product of two numbers is equal to the product of their LCM and HCF.
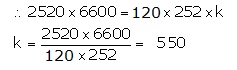
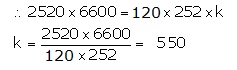
Q25.  is
is
 is
is Solution
Q26. Which of the following rational number has a terminating decimal expansion?
Solution
Q27. Show that any positive even integer is of the form 6m, 6m + 2 or 6m + 4, where m is some integer.
Solution
Let a and b be any positive integers,
a = bm + r, 0 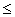 r <b
Let b = 6. Then, r = 0,1,2,3,4,5
r <b
Let b = 6. Then, r = 0,1,2,3,4,5
 a = 6m + r, where r = 0, 1, 2, 3, 4, 5
When r = 0, a = 6m even
When r = 1a = 6m + 1odd
When r = 2a = 6m + 2even
When r = 3a = 6m + 3odd
When r = 4a = 6m + 4even
When r = 5a = 6m + 5odd
Hence, all positive even integers are of the form 6m, 6m + 2 or 6m + 4.
a = 6m + r, where r = 0, 1, 2, 3, 4, 5
When r = 0, a = 6m even
When r = 1a = 6m + 1odd
When r = 2a = 6m + 2even
When r = 3a = 6m + 3odd
When r = 4a = 6m + 4even
When r = 5a = 6m + 5odd
Hence, all positive even integers are of the form 6m, 6m + 2 or 6m + 4.
Q28. 1192 - 1112 is:
Solution
1192 - 1112 = (119 + 111) (119 - 111) = 230 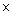 8 (Even number)
Hence, 1192 - 1112 is a composite number, since a composite number has more than 2 factors other than itself and 1.
8 (Even number)
Hence, 1192 - 1112 is a composite number, since a composite number has more than 2 factors other than itself and 1.
Q29. Find
HCF of 1288 and 575 by using Euclid’s Division Algorithm.
Solution
In the given
pair, 1288 > 575, thus let 1288 = a and 575 = b.
Now by applying
the Euclid’s division algorithm a = bq + r, we get
1288 = 575 × 2 + 138
575 = 138 × 4 + 23
138= 23 × 6 + 0
Since in the
above equation we get r = 0;
Therefore, 23 is
the HCF of the given pair 1288 and 575.
Q30. Find
HCF of 35, 56 and 91.
Solution
First find the HCF of 35
and 56.
56 =
35 ×
1 +
21
35 =
21 ×
1 +
14
21 =
14 ×
1 +
7
14 =
7 ×
2 + 0
So, HCF (35, 56) =
7
Now, HCF (7, 91)
91 =
7 ×
13 +
0
So, HCF (7, 91) =
7
Therefore, HCF (35, 56,
91) =
7
Hence, HCF of 35, 36, 91 is 7.
Q31. Find
HCF of 963 and 657 by using Euclid’s Division Algorithm.
Solution
In the given pair, 963 > 657, thus let
963 = a and 657 = b.
Now by applying Euclid’s division
algorithm a = bq + r, we get
963 = 657 × 1 + 306
657 = 306 × 2 + 45
306 = 45 × 6 + 36
45 = 36 × 1 + 9
36 = 9 × 4 + 0
Since in the above equation we get r
= 0; therefore, 9 is the HCF of the given pair 963 and 657.
Q32. Find
HCF of 24, 15 and 36.
Solution
First find the HCF of 24
and 15.
24 =
15 ×
1 +
9
15 =
9 ×
1 + 6
9 =
6 ×
1 +
3
So, HCF (24, 15) =
3
Now, HCF (3, 36)
36 = 3 ×
13 +
0
So, HCF (3, 36) =
3
Therefore, HCF (24, 15,
36) =
3
Q33. Euclid's division lemma states that if a and b are two positive integers, then there exist unique integers q and r such that:
Solution
Recall Euclid's division lemma.
Euclid's division lemma states that if a and b are two positive integers, then there exist unique integers q and r such that:
a = bq + r, 0 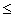 r <b
r <b
Q34. Prove that 7 - 2 is irrational.
is irrational.
Solution
Suppose 7 - 2 is rational.
is rational.
 7 -
7 - 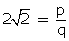 , where q
, where q  0, p and q are co-prime
0, p and q are co-prime
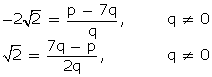 But
But  is irrational while
is irrational while 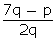 is rational and an irrational number can never be equal to a rational number. Thus, our assumption is wrong and hence 7 -
is rational and an irrational number can never be equal to a rational number. Thus, our assumption is wrong and hence 7 - 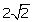 is irrational.
is irrational.
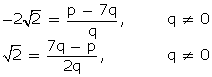 But
But
Q35. If the HCF of 85 and 153 is expressible in the form 85n - 153, then value of n is :
Solution
HCF of 85 and 153 :
153 = 85 x 1 + 68
85 = 68 x 1 + 17
68 = 17 x 4 + 0
HCF of (85, 153) = 17
It is given that the HCF is expressible as 85n - 153.
 85n - 153 = 17
85n = 17 + 153 = 170
n =
85n - 153 = 17
85n = 17 + 153 = 170
n =  = 2
= 2
 = 2
= 2
Q36. The decimal expansion of 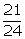 will terminate after how many places of decimal?
will terminate after how many places of decimal?
Solution
Q37. prove that 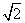 is irrational number.
is irrational number.
Solution
Let us assume, to the contrary that 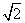 is rational
is rational
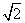 =
=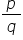 or
or 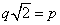
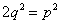 --- (1)
Therefore 2 divides
--- (1)
Therefore 2 divides 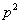 and 2 divides p.
So we can write p = 2r for some integer r
Substituting this value of p = 2r in (1), we get
and 2 divides p.
So we can write p = 2r for some integer r
Substituting this value of p = 2r in (1), we get
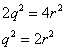 This means 2 divides to
This means 2 divides to  or 2 divides q also.
Therefore, p and q have at least 2 as a common factor.
But this contradict the fact that p and q have no common factor other than 1.
This contradiction arises because of our wrong assumption that
or 2 divides q also.
Therefore, p and q have at least 2 as a common factor.
But this contradict the fact that p and q have no common factor other than 1.
This contradiction arises because of our wrong assumption that 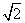 is a rational number.
So we conclude that
is a rational number.
So we conclude that 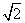 is irrational number.
is irrational number.
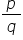 or
or 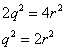 This means 2 divides to
This means 2 divides to
Q38. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution
Let x be the maximum number of columns is which the two groups can march, then x is HCF of 616 and 32.
Here 616 > 32
By Euclid division algorithm,
616 = 32 × 19 + 8
32 = 8 × 4 + 0
Thus, HCF (616, 32) = 8
Hence the maximum number of columns in which they can march is 8.
Q39. Use Euclid's division lemma to show that cube of any positive integer is either of form 9q, 9q + 1, or 9q + 8 for some integer q.
Solution
Let a be any positive integer and b = 3
a = 3m + r, where 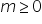 and
and 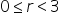
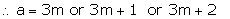 Therefore, every number can be represented as these three forms. There are three cases.
Case 1: When a = 3m,
Therefore, every number can be represented as these three forms. There are three cases.
Case 1: When a = 3m,
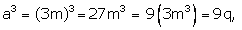 Where q is an integer such that q =
Where q is an integer such that q = 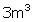 Case 2: When a = 3m + 1,
a3 = (3m +1)3
a3 = 27m3 + 27m2 + 9m + 1
a3 = 9(3m3 + 3m2 + m) + 1
a3 = 9q + 1
Where q is an integer such that q = (3m3 + 3m2 + m)
Case 3: When a = 3m + 2,
a3 = (3m + 2)3
a3 = 27m3 + 54m2 + 36m + 8
a3 = 9(3m3 + 6m2 + 4m) + 8
a3 = 9q + 8
Where q is an integer such that q = (3m3 + 6m2 + 4m)
Hence, the cube of any positive integer is of the form 9q, 9q + 1, or 9q + 8.
Case 2: When a = 3m + 1,
a3 = (3m +1)3
a3 = 27m3 + 27m2 + 9m + 1
a3 = 9(3m3 + 3m2 + m) + 1
a3 = 9q + 1
Where q is an integer such that q = (3m3 + 3m2 + m)
Case 3: When a = 3m + 2,
a3 = (3m + 2)3
a3 = 27m3 + 54m2 + 36m + 8
a3 = 9(3m3 + 6m2 + 4m) + 8
a3 = 9q + 8
Where q is an integer such that q = (3m3 + 6m2 + 4m)
Hence, the cube of any positive integer is of the form 9q, 9q + 1, or 9q + 8.
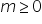 and
and 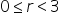
Q40. Find the largest number that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively.
Solution
Find the largest number that will divide 398, 436 and 542 leaving remainder 7, 11 and 15 respectively.
Clearly, the required number is the H.C.F of 398 - 7 = 391, 436 - 11 = 425 and 542 - 15 = 527.
From 391, 425 and 527, we will take 391 and 425.
Here 425 > 391
425 = 391 × 1 + 34
391 = 34 × 11 + 17
34 = 17 × 11 + 0
Now the remainder is zero.
 Now we will find the HCF of 527 and 17.
527 = 17 × 31 + 0
Now the remainder is zero.
Now we will find the HCF of 527 and 17.
527 = 17 × 31 + 0
Now the remainder is zero.
 Hence largest number i.e the required number is 17.
Hence largest number i.e the required number is 17.
 Now we will find the HCF of 527 and 17.
527 = 17 × 31 + 0
Now the remainder is zero.
Now we will find the HCF of 527 and 17.
527 = 17 × 31 + 0
Now the remainder is zero.
 Hence largest number i.e the required number is 17.
Hence largest number i.e the required number is 17.
Q41. Find
HCF of 506 and 1155 by using Euclid’s Division Algorithm.
Solution
In
the given pair, 1155 > 506, thus let 1155 = a and
506 = b.
Now
by applying the Euclid’s division algorithm
A
= bq + r, we get
1155
= 506 × 2 + 143
506
= 143 × 3 + 77
143
= 77 × 1 + 66
77 = 66 × 1 + 11
66 = 11 × 6 + 0
Since
in the above equation we get r = 0; therefore, 11 is the HCF of the given
pair 1155 and 506.
Q42. State why  is a non-terminating repeating decimal.
is a non-terminating repeating decimal.
Solution
62 × 53 = (2 × 3)2 × 53 = 22 × 32 × 53
The prime factorization of the denominator contains a prime factor 3 other than 2 and 5.
Therefore the decimal expansion of a given rational number is non - terminating repeating.
Q43. To prove  is an irrational number, which of the following methods is used?
is an irrational number, which of the following methods is used?
 is an irrational number, which of the following methods is used?
is an irrational number, which of the following methods is used? Solution
To prove  is an irrational number, the contradictory method is used.
is an irrational number, the contradictory method is used.
 is an irrational number, the contradictory method is used.
is an irrational number, the contradictory method is used.
Q44. H.C.F. of two consecutive even numbers is:
Solution
We know that 2 is a factor of all the even numbers.
Consider an even number, say 2q.
This number will have its next consecutive even number as 2q+2
Further, this number will have its consecutive even number are 2q + 2 + 2= 2q + 4
2q + 2 can be written as 2(q+1), while 2q + 4 can be written as 2(q+2).
So, the only common factor is 2.
The HCF of two consecutive even numbers is 2.
Q45. If two positive integers A and B can be expressed as A = ab2 and B = a3b, where a and b are prime numbers, then LCM (A, B) is:
Solution
A = ab2 and B = a3b
LCM (A, B) = a3b2
Q46. Find the HCF of 117 and
45 by Euclid’s division lemma.
Solution
117 = 45 × 2 + 27
45 = 27 × 1 + 18
27 = 18 × 1 + 9
18 = 9 × 2 + 0
So, the HCF of 117 and
45 by Euclid’s division lemma is 9.
Q47. Show that 4n can never end with the digit zero for any natural number n.
Solution
Hence 4n can never end with the digit zero for any n  N.
We have 4n, where n = 1, 2, 3, 4, ...
If n = 1 then 4n = 41 = 4
If n = 2 then 4n = 42 = 16
and so on.
If a number ends with zero then it is divisible by 5.
Here, 4 and 16 are not divisible by 5.
Therefore, 4n can never end with zero fro any natural number n.
N.
We have 4n, where n = 1, 2, 3, 4, ...
If n = 1 then 4n = 41 = 4
If n = 2 then 4n = 42 = 16
and so on.
If a number ends with zero then it is divisible by 5.
Here, 4 and 16 are not divisible by 5.
Therefore, 4n can never end with zero fro any natural number n.
Q48. Show that every positive even integer is of the form 2q and that every positive odd integer is of the form 2q + 1, where q is some integer.
Solution
By Euclid's lemma,
a = bq + r, 0 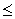 r < b, a, b, q are integers.
Let b = 2
r < b, a, b, q are integers.
Let b = 2
 a = 2q when r = 0, this is an even number
and a = 2q + 1, when r = 1, which is an odd number.
a = 2q when r = 0, this is an even number
and a = 2q + 1, when r = 1, which is an odd number.
Q49. Find the H.C.F. and L.C.M. of 6, 72 and 120 using the prime factorisation method.
Solution
6 = 2 x 3
72 = 2 x 2 x 2 x 3 x 3
120= 2 x 2 x 2 x 3 x 5
Marking the factors common to all the three numbers, we see that the HCF = 2 X 3=6
LCM = 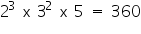
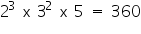
Q50. D is a point on the side BC of ΔABC such that ∠ADC = ∠BAC. Prove that CA2 = CB × CD.
OR
Prove that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side.
Solution
 (1)
In ΔABC and ΔDAC,
∠ADC = ∠BAC and ∠C = ∠C
According to the AA-criterion of similarity,
ΔABC ≅ ΔDAC (1)
(1)
In ΔABC and ΔDAC,
∠ADC = ∠BAC and ∠C = ∠C
According to the AA-criterion of similarity,
ΔABC ≅ ΔDAC (1)
 Given: Triangle ABC in which D and E are the midpoints of AB and AC, respectively.
To prove: DE is parallel to BC. (1)
Proof :
Since D and E are the midpoints of AB and AC, respectively.
We have AD = DB and AE = EC.
∴
Given: Triangle ABC in which D and E are the midpoints of AB and AC, respectively.
To prove: DE is parallel to BC. (1)
Proof :
Since D and E are the midpoints of AB and AC, respectively.
We have AD = DB and AE = EC.
∴
Q51. Prove that 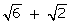 is irrational.
is irrational.
Solution
Let us suppose that 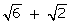 is rational.
Then,
is rational.
Then, 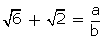 where a and b are integers and b
where a and b are integers and b 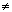 0
8 + 2
0
8 + 2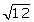 =
= 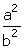 8 + 4
8 + 4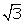 =
= 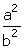
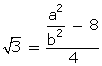 Since, a, b, 8 and 4 are integers,
Since, a, b, 8 and 4 are integers, 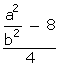 is rational.
is rational.
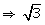 is a rational number.
But we know that
is a rational number.
But we know that 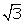 is irrational.
is irrational.
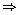 irrational = rational, which is a contradiction
Hence,
irrational = rational, which is a contradiction
Hence, 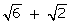 is an irrational.
is an irrational.
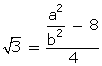 Since, a, b, 8 and 4 are integers,
Since, a, b, 8 and 4 are integers, 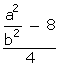 is rational.
is rational.
Q52. Prove that  is irrational.
is irrational.
Solution
Suppose  is rational.
is rational.

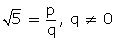 and HCF (p, q) = 1
5q2 = p2.... (1)
5 is a factor of p2, therefore, 5 is a factor of p.
Now, suppose p = 5
and HCF (p, q) = 1
5q2 = p2.... (1)
5 is a factor of p2, therefore, 5 is a factor of p.
Now, suppose p = 5 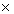 m
From (1), 5q2 = 25 m2
q2 = 5 m2
m
From (1), 5q2 = 25 m2
q2 = 5 m2
 5 is a factor of q2 and therefore 5 is a factor of q.
Thus, 5 is a common factor of p and q, which contradicts to our assumption of HCF (p, q) = 1
Hence,
5 is a factor of q2 and therefore 5 is a factor of q.
Thus, 5 is a common factor of p and q, which contradicts to our assumption of HCF (p, q) = 1
Hence,  is irrational.
is irrational.
Q53. Find
HCF of 155 and 1385 by using Euclid’s Division Algorithm.
Solution
In
the given pair, 1385 > 155, thus let
1385 = a and 155 = b.
Now
by applying the Euclid’s division algorithm a = bq
+ r, we get
1385
= 155 × 8 + 145
155
= 145 × 1 + 10
145
= 10 × 14 + 5
10
= 10 × 2 + 0
Since
in the above equation we get r = 0; therefore, 5is the HCF of the given pair
1385 and 155.
Q54. Prove that 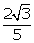 is irrational.
is irrational.
Solution
Let 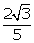 be a rational number.
Then,
be a rational number.
Then,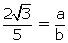 ,
Where a and b are co-prime and b
,
Where a and b are co-prime and b  0
0
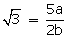 As a and b are integers,
As a and b are integers, 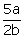 is a rational number
is a rational number
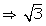 is rational
This is a contradiction as
is rational
This is a contradiction as 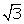 is irrational.
is irrational.
 is irrational.
is irrational.
Q55. Find
the HCF of 876 and 255 by Euclid’s division lemma.
Solution
876
= 225 × 3 + 111
225
= 111 × 2 + 3
111
=
3
× 37 + 0
Hence,
HCF of 876 and 255 is 3.
Q56. The radius and height of a cylinder are in the ratio 2:7. If the curved surface area of the cylinder is 352 sq. cm, find its radius.
Solution
Let the radius be 2x and height be 7x.
Curved surface area = 352 cm2
2πrh = 352 (½)
 88x2 = 352
88x2 = 352
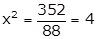 (1)
x = 2
Radius = 2 × 2 = 4 cm (½)
(1)
x = 2
Radius = 2 × 2 = 4 cm (½)
Q57. Prove that 5 + 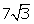 is an irrational number.
OR
Prove that
is an irrational number.
OR
Prove that 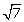 is an irrational number.
is an irrational number.
Solution
Let 5 + 7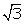 be a rational number.
Then,
5 + 7
be a rational number.
Then,
5 + 7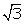 =
= 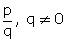 7
7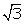 =
= 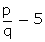
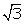 =
= 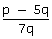 Since, p and q are integers,
Since, p and q are integers,  is a rational number.
Therefore,
is a rational number.
Therefore, 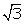 is also a rational number.
This is a contradiction as we know that
is also a rational number.
This is a contradiction as we know that 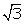 is irrational.
is irrational.
 Out assumption is wrong.
Hence, 5 + 7
Out assumption is wrong.
Hence, 5 + 7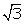 is irrational.
OR
Let
is irrational.
OR
Let 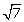 be a rational number.
Let
be a rational number.
Let 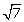 =
= 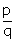 , where q
, where q  0, p and q are integers and are co-prime.
0, p and q are integers and are co-prime.
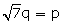 7 q2 = p2
Thus, 7 divides p2 and hence 7 divides p.
Let p = 7m
7 q2 = p2
Thus, 7 divides p2 and hence 7 divides p.
Let p = 7m
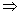 7q2 = 49 m2
7q2 = 49 m2
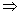 q2 = 7m2
q2 = 7m2
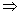 7 divides q2
7 divides q2 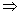 7 divides q
7 divides q
 7 divides p and q both.
This is a contradiction as p and q are co-prime.
Hence,
7 divides p and q both.
This is a contradiction as p and q are co-prime.
Hence, 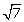 is an irrational number.
is an irrational number.
Q58. Find the HCF of 70 and 30 by
Euclid’s division lemma.
Solution
70 = 30 × 2 + 10
30 = 10 × 3 + 0
Hence, HCF of 70 and 30 is 10.
Q59. Find
the HCF of 135 and 225 by Euclid’s division lemma.
Solution
225 = 135 × 1 + 90
135 = 90 × 1 + 45
90 = 45 × 2 + 0
Hence, HCF of 135 and 225 is 45.
Q60. Find
HCF of 84, 90 and 120.
Solution
First find the HCF of 84
and 90.
90 =
84 ×
1 +
6
84 =
6 ×
14 +
0
So, HCF (90, 84) =
6
Now, HCF (6, 120)
120 =
6 ×
20 +
0
So, HCF (6, 120) =
6
Therefore, HCF (84, 90,
120) =
6
Q61. Find the HCF of 105 and 120 by
Euclid’s division lemma.
Solution
120 = 105 × 1 + 15
105 = 15 × 7 + 0
Hence, HCF of 105 and 120 is 15.
Q62. For the decimal number  , the rational number is:
, the rational number is:
Solution
Let x =  Then, x = 0.7777…………(1)
Here, the number of digits recurring is only 1, so we multiply both sides of the equation by 10.
Then, x = 0.7777…………(1)
Here, the number of digits recurring is only 1, so we multiply both sides of the equation by 10.
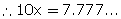 …….(2)
Subtracting (1) from (2), we get:
9x = 7
…….(2)
Subtracting (1) from (2), we get:
9x = 7
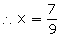
Q63. If d is the HCF of 45 and 27, find x, y satisfying d = 27x + 45y.
Solution
Since 45 > 27
By applying Euclid's division Lemma to 27 and 45, we get,
45 = 27 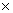 1 + 18
27 = 18
1 + 18
27 = 18 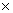 1 + 9
18 = 9
1 + 9
18 = 9 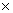 2 + 0
The remainder has now become zero, so we will stop the procedure.
Since the divisor at this stage is 9.
HCF (45, 27) = 9
9 = 27 - 18
= 27 - (45 - 27
2 + 0
The remainder has now become zero, so we will stop the procedure.
Since the divisor at this stage is 9.
HCF (45, 27) = 9
9 = 27 - 18
= 27 - (45 - 27 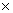 1)
= 27 - 45 + 27
= 54 - 45
= 27
1)
= 27 - 45 + 27
= 54 - 45
= 27 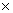 2 - 45
2 - 45 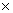 1
Comparing this with d = 27x + 45y, we get,
x = 2, y = -1
1
Comparing this with d = 27x + 45y, we get,
x = 2, y = -1
Q64. If x = 23 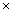 3
3 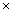 52, y = 22
52, y = 22 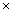 32, then HCF (x, y) is :
32, then HCF (x, y) is :
Solution
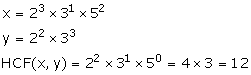
Q65. Find the HCF and LCM of 336 and 54. Verify that HCF 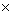 LCM = Product of the two number.
LCM = Product of the two number.
Solution
336 = 2 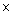 2
2 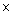 2
2 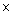 2
2 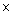 3
3 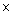 7
54 = 2
7
54 = 2 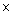 3
3 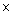 3
3 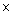 3
HCF (336, 54) = 2
3
HCF (336, 54) = 2 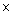 3 = 6
LCM (336, 54) = 24
3 = 6
LCM (336, 54) = 24 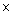 33
33 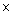 7 = 3024
Verification:
HCF
7 = 3024
Verification:
HCF 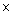 LCM = 6
LCM = 6 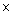 3024 = 18144
Product of numbers = 336
3024 = 18144
Product of numbers = 336 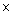 54 = 18144
54 = 18144
Q66. A man observes a bird in the east flying at an angle of elevation 30°. After 2 minutes, he observes that the bird has flown west at an angle of elevation 60°. If the bird flies in a straight line all along at a height h√3, find the speed of the bird.
OR
A bridge across a river makes an angle of 45° with the river bank. If the length of the bridge across the river is 150 m, what is the width of the river?
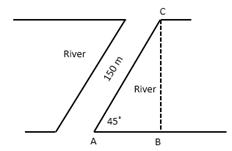

Solution
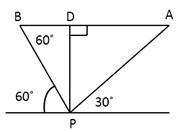 In triangle BPD, tan 60˚ =
In triangle BPD, tan 60˚ =  (1)
Hence, the width of the river is
(1)
Hence, the width of the river is
Q67. Show that
2√3 is irrational.
Solution
If possible,
let 2√3 be rational.
Let its
simplest form be 2√3 = a/b, where a and b are
positive integers having no common factor other than 1.
Then,
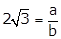
 Since a and 2b are non-zero integers,
Since a and 2b are non-zero integers, 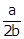 is rational. (1)
Thus, from (i), it follows that √3 is rational.
This
contradicts the fact that √3 is irrational.
The
contradiction arises by assuming that 2√3 is rational.
Hence, 2√3
is irrational. (1)
is rational. (1)
Thus, from (i), it follows that √3 is rational.
This
contradicts the fact that √3 is irrational.
The
contradiction arises by assuming that 2√3 is rational.
Hence, 2√3
is irrational. (1)
Q68. Find the H.C.F. and L.C.M. of 6, 72 and 120 using the prime factorisation method.
Solution

Q69. The areas of
two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5 cm, find
the length of QR.
Solution
Since
∆ABC ~ ∆PQR,
According
to the question,
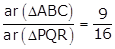

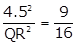 (½)
(½)
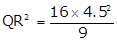 QR2 = 36
QR = 6 (½)
QR2 = 36
QR = 6 (½)
Q70. show that 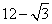 is irrational.
is irrational.
Solution
Let 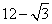 =
=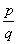 a rational number
a rational number
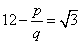 rearranging this equation
rearranging this equation 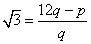 Since 12 and
Since 12 and 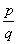 are rational number which mean
are rational number which mean 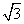 is also a rational number. But this contradicts the fact that
is also a rational number. But this contradicts the fact that 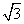 is an irrational because we already learnt that square roots of prime numbers are irrational. So, we conclude that
is an irrational because we already learnt that square roots of prime numbers are irrational. So, we conclude that 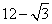 is irrational.
is irrational.
Q71. A proven statement used
for proving another statement is called
Solution
A
proven statement used for proving another statement is called a lemma.
Q72. Prove that 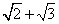 is an irrational number.
is an irrational number.
Solution
Suppose 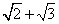 is not an irrational number, then it must be a rational number.
So let
is not an irrational number, then it must be a rational number.
So let  =q where q is a rational number.
=q where q is a rational number.
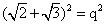
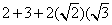 )=
)=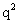
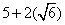 =
=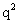
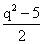 =
=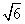 So here we have an equation with its left side is a rational number(as the set of rational numbers is closed under subtraction and division i.e the subtraction and division of two rational numbers is always a rational number)and so its right side must also be a rational number.
So here we have an equation with its left side is a rational number(as the set of rational numbers is closed under subtraction and division i.e the subtraction and division of two rational numbers is always a rational number)and so its right side must also be a rational number.
 is a rational number
Which is a contradiction. So our basic assumption must be wrong.
is a rational number
Which is a contradiction. So our basic assumption must be wrong.
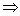
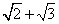 =q where q is a rational number,is wrong
=q where q is a rational number,is wrong
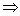
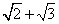 is an irrational number.
Hence proved.
is an irrational number.
Hence proved.
Q73. Show that 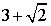 is irrational.
is irrational.
Solution
Let us assume that 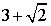 is a rational i.e.
is a rational i.e.  Or,
Or,  Here
Here 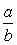 and 3 both are rational and we know that the difference of two rational is always rational.
this is a contradiction to our assumption.
hence,
and 3 both are rational and we know that the difference of two rational is always rational.
this is a contradiction to our assumption.
hence,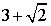 is not rational, i.e. it is an irrational number
is not rational, i.e. it is an irrational number
Q74. Find the HCF of 1000 and 1125.
Solution
1125
= 1000 × 1 + 125
1000
= 125 × 8 + 0
Hence,
HCF of 1000 and 1125 is 125.
Q75. Find the
value of k for which x = 2 is a solution of the equation kx2 + 2x - 3 = 0.
Solution
It is given that 2 is a
solution of the quadratic equation kx2 + 2x - 3 = 0.
Hence,
k × 22 + 2 × 2 - 3 = 0 (½)
4k = −1
k =
−1/4 (½)
Q76. Find the HCF and LCM of 72 and 120 using prime factorization.
Solution
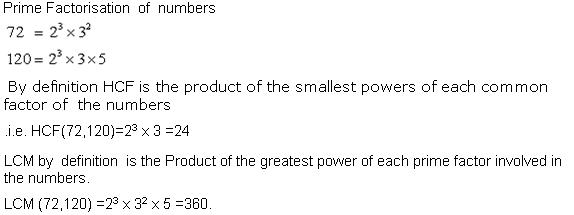
Q77. Given that HCF(306,657) = 9 ,find LCM(306,657).
Solution
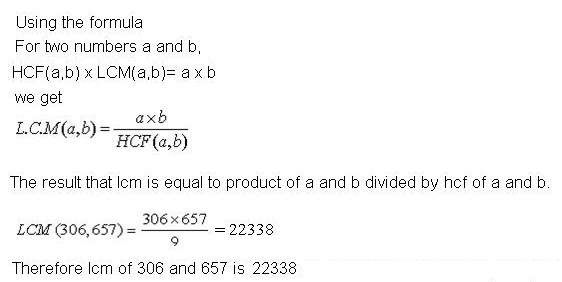
Q78. The expression 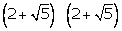 is :
is :
Solution
Q79. A series of well-defined
steps which give a procedure for solving a type of problem is called
Solution
A series of well-defined
steps which give a procedure for solving a type of problem is called an
algorithm.
Q80. Using Euclid Division Lemma, prove that for any positive integer n, n3 - n is divisible by 6.
Solution
Any positive integer is of the form 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4, 6m + 5 for some positive integer n.
When n = 6m,
n3 - n = (6m)3 - 6m
= 216m3 - 6m
= 6m(36m2 - 1)
= 6q, where q = m(36m2 -1)
 n3 - n is divisible by 6
When n = 6m + 1,
n3 - n = n(n2 - 1)
= n (n - 1) (n + 1)
= (6m + 1) (6m) (6m + 2)
= 6m(6m + 1) (6m + 2)
= 6q, where q = m(6m + 1) (6m + 2)
n3 - n is divisible by 6
When n = 6m + 1,
n3 - n = n(n2 - 1)
= n (n - 1) (n + 1)
= (6m + 1) (6m) (6m + 2)
= 6m(6m + 1) (6m + 2)
= 6q, where q = m(6m + 1) (6m + 2)
 n3 - n is divisible by 6
When n = 6m + 2,
n3 - n = n (n - 1) (n + 1)
= (6m + 2) (6m + 1) (6m + 3)
= (6m + 1) (36 m2 + 30m + 6)
= 6m (36 m2 + 30m + 6) + 1 (36m2 + 30m + 6)
= 6[m (36m2 + 30m + 6)] + 6 (6m2 + 5m + 1)
= 6p + 6q, where p = m (36m2 + 30m + 6) and q = 6m2 + 5m + 1
n3 - n is divisible by 6
When n = 6m + 2,
n3 - n = n (n - 1) (n + 1)
= (6m + 2) (6m + 1) (6m + 3)
= (6m + 1) (36 m2 + 30m + 6)
= 6m (36 m2 + 30m + 6) + 1 (36m2 + 30m + 6)
= 6[m (36m2 + 30m + 6)] + 6 (6m2 + 5m + 1)
= 6p + 6q, where p = m (36m2 + 30m + 6) and q = 6m2 + 5m + 1
 n3 - n is divisible by 6
When n = 6m + 3
n3 - n = (6m + 3)3 - (6m + 3)
= (6m + 3) [(6m + 3)2 - 1]
= 6m [6m + 3)2 - 1] + 3 [(6m + 3)2 - 1]
=6 [m [(6m + 3)2 - 1] + 3 [36m2 + 36m + 8]
=6 [m [(6m + 3)2 - 1] + 6 [18m2 + 18m + 4]
= 6p + 3q, where p = m[(6m + 3)2 - 1] and q = 18m2 + 18m + 4
n3 - n is divisible by 6
When n = 6m + 3
n3 - n = (6m + 3)3 - (6m + 3)
= (6m + 3) [(6m + 3)2 - 1]
= 6m [6m + 3)2 - 1] + 3 [(6m + 3)2 - 1]
=6 [m [(6m + 3)2 - 1] + 3 [36m2 + 36m + 8]
=6 [m [(6m + 3)2 - 1] + 6 [18m2 + 18m + 4]
= 6p + 3q, where p = m[(6m + 3)2 - 1] and q = 18m2 + 18m + 4
 n3 - n is divisible by 6
When n = 6m + 4
n3 - n = (6m + 4)3 - (6m + 4)
= (6m + 4) [(6m + 4)2 - 1]
= 6m [(6m + 4)2 - 1] + 4 [(6m + 4)2 - 1]
= 6m [(6m + 4)2 - 1] + 4 [36m2 + 48m + 16 - 1]
= 6m [(6m + 4)2 - 1] + 12 [12m2 + 16m + 5]
= 6p + 6q, where p = m [(6m + 4)2 - 1] and q = 2 (12 m2 + 16m + 5)
n3 - n is divisible by 6
When n = 6m + 4
n3 - n = (6m + 4)3 - (6m + 4)
= (6m + 4) [(6m + 4)2 - 1]
= 6m [(6m + 4)2 - 1] + 4 [(6m + 4)2 - 1]
= 6m [(6m + 4)2 - 1] + 4 [36m2 + 48m + 16 - 1]
= 6m [(6m + 4)2 - 1] + 12 [12m2 + 16m + 5]
= 6p + 6q, where p = m [(6m + 4)2 - 1] and q = 2 (12 m2 + 16m + 5)
 n3 - n is divisible by 6
When n = 6m + 5
n3 - n = (6m + 5) [(6m + 5)2 - 1]
= 6m [(6m + 5)2 - 1] + 5 [(6m + 5)2 - 1]
= 6m [(6m + 5)2 - 1] + 5 [36m2 + 60m + 24]
= 6p + 30q
= 6(p + 5q), where p = m [(6m + 5)2 - 1] and q = 6m2 + 10m + 4
n3 - n is divisible by 6
When n = 6m + 5
n3 - n = (6m + 5) [(6m + 5)2 - 1]
= 6m [(6m + 5)2 - 1] + 5 [(6m + 5)2 - 1]
= 6m [(6m + 5)2 - 1] + 5 [36m2 + 60m + 24]
= 6p + 30q
= 6(p + 5q), where p = m [(6m + 5)2 - 1] and q = 6m2 + 10m + 4
 n3 - n is divisible by 6
Hence, n3 - n is divisible by 6, for any +ve integer n.
n3 - n is divisible by 6
Hence, n3 - n is divisible by 6, for any +ve integer n.
Q81. Show that the square of any positive integer cannot be of the form 5q + 2 or 5q + 3 for any integer q.
Solution
Let a be any positive integer.
By Euclid's division lemma,
a = bm + r where b = 5
⇒ a = 5m + r
So, r can be any of 0, 1, 2, 3, 4
∴ a = 5m when r = 0,
a = 5m + 1 when r = 1,
a = 5m + 2 when r = 2,
a = 5m + 3 when r = 3,
a = 5m + 4 when r = 4
Case I : a = 5m
⇒ a2 = (5m)2 = 25m2
⇒ a2 = 5(5m2) = 5q, where q = 5m2
Case II : a = 5m + 1
⇒ a2 = (5m + 1)2 = 25m2 + 10 m + 1
⇒ a2 = 5 (5m2 + 2m) + 1 = 5q + 1, where q = 5m2 + 2m
Case III : a = 5m + 2
⇒ a2 = (5m + 2)2
⇒ a2 = 25m2 + 20m + 4
⇒ a2 = 5 (5m2 + 4m) + 4
⇒ a2 = 5q + 4 where q = 5m2 + 4m
Case IV: a = 5m + 3
⇒ a2 = (5m + 3)2 = 25m2 + 30m + 9
⇒ a2 = 5 (5m2 + 6m + 1) + 4
⇒ a2 = 5q + 4 where q = 5m2 + 6m + 1
Case V: a = 5m + 4
⇒ a2 = (5m + 4)2 = 25m2 + 40m + 16
⇒ a2 = 5 (5m2 + 8m + 3) + 1
⇒ a2 = 5q + 1 where q = 5m2 + 8m + 3
From all these cases, it is clear that square of any positive integer cannot be of the form 5q + 2 or 5q + 3.
Q82. The 6th term of an AP is −10 and its 10th term is −26. Determine the 15th term of the AP.
Solution
In the given AP, let the first term = a and the common difference = d.
Tn = a + (n - 1)d
T6 = a + (6 - 1)d and T10 = a + (10 - 1)d
T6 = a + 5d and T10 = a + 9d (1)
−10 = a + 5d … (i)
−26 = a + 9d … (ii)
On subtracting (i) from (ii), we get
4d = −16, then d = −4
On substituting d = −4 in (i), we get
a + 5 (−4) = −10 (1)
a = 10
Thus, a = 10 and d = −4
15th term = T15
= a + 14d
= 10 + 14 × (−4)
= −46 (2)
Q83. Prove that 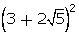 is irrational.
is irrational.
Solution
Let us assume that 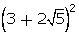 =
= 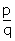 Where p and q are co-prime integers, q
Where p and q are co-prime integers, q 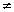 0
0

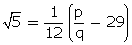 Since, p and q are integers, RHS is rational.
So, LHS =
Since, p and q are integers, RHS is rational.
So, LHS = 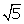 is also rational.
This contradicts the fact that
is also rational.
This contradicts the fact that 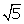 is irrational.
Thus, our assumption was wrong.
Hence,
is irrational.
Thus, our assumption was wrong.
Hence, 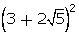 is irrational.
is irrational.

Q84. From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
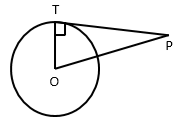

Solution
According to the question,
OP = 10 cm
PT = 8 cm
PT is tangent at T and OT is the radius through T.
OT is perpendicular to PT.
In the right-angled triangle OTP,
OP2 = OT2 + PT2 (by Pythagoras theorem) (½)
OT2 = OP2 - PT2
OT = 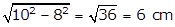 (1)
Hence, the radius of the circle is 6 cm. (½)
(1)
Hence, the radius of the circle is 6 cm. (½)
Q85. A sweet seller has 867 kaju barfis and 255 badam barfies. She wants to stack them in such a way that each stack has the same number and they take up the least area of the tray. What is the number of that can be placed in each stack for this purpose?
Solution

Q86. There is a circular path around a sports field whose circumference is 5280 m. A cycle at the speed 330m/min of the field B at the speed of 220 m/min and C at the speed of 165 m/min. If A,B and C all starts from the same point, then after how many minutes they will be together at the same starting point?
Solution

Q87. If d is the HCF of 45 and 27, find x, y satisfying d = 27x + 45y.
Solution
Here 45 > 27
By Applying Euclid's division Lemma to 27 and 45 we get,
45 = 27 × 1 + 18
27 = 18 × 1 + 9
18 = 9 × 2 + 0
HCF(27, 45) = 9
9 = 27 - 18 × 1
= 27 - (45 - 27 )×1
= 27 - 45 × 1 + 27 ×1
= 27 - 45 + 27
= 54 - 45
= 27 ×2 - 45 ×1
Comparing this with d = 27x + 45y, we get,
x = 2, y = -1, d = 9
Q88. There is a circular path around a sports field. Sonia takes 18 minute to drive one round of the field while Ravi takes 12 minute for the same. Suppose they both start at the same point and at the same time and go in same direction. After how many minutes will they meet at the starting point.
Solution
Required number of minutes is the L.C.M of 18 and 12.
We have 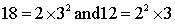 LCM is
Product of the greatest power of each prime factor involved in the numbers.
LCM is
Product of the greatest power of each prime factor involved in the numbers.
 L.C.M of 18 and 12 =
L.C.M of 18 and 12 = 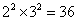
 Hence Sonia and Ravi will meet after 36 min.
Hence Sonia and Ravi will meet after 36 min.
Q89. Draw a circle of radius 4 cm. Take a point P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
Solution
Steps of construction:
Draw a line segment 4 cm.
Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
Produce AP to C such that AP = CP.
Draw a semi-circle with CB as diameter.
Draw PD perpendicular to CB, intersecting the semi-circle at D.
With P as centre and PD as radius, draw arcs to intersect the given circle at T and M.
Join PT and PM.
Then PT and PM are the required tangents.
 NOTE: Correct construction of circle = 1 mark
Correct construction of tangents = 3 marks
NOTE: Correct construction of circle = 1 mark
Correct construction of tangents = 3 marks
 NOTE: Correct construction of circle = 1 mark
Correct construction of tangents = 3 marks
NOTE: Correct construction of circle = 1 mark
Correct construction of tangents = 3 marks
Q90. Find the LCM and HCF of 15, 18, 45 by the prime factorisation method.
Solution
 15 = 3
15 = 3
Q91. In the
figure below, triangle ABC is circumscribed touching the circle at P, Q, R. If AP = 4 cm, BP = 6 cm, AC = 12 cm and BC = x cm, find
x.
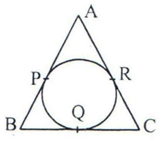

Solution
Since the lengths of
tangents drawn from an external point to a circle are equal,
AC = 12
AR + RC = 12
4 + RC = 12
RC = 12 - 4 = 8 cm
CR = CQ = 8 cm
BP = BQ = 6 cm (½)
BC = x
BQ + CQ = x
8 + 6 = x
x = 14 cm (½)
Q92. 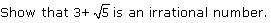
Solution

Q93. Is 523 a prime number? Justify your answer.
Solution
523 lies between 484 and 529 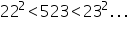 Prime numbers less than 23 are 2,3,5,7,11,13,17,19Since 523 is not divisible by any of these numbers Hence, 523 is a prime number
Prime numbers less than 23 are 2,3,5,7,11,13,17,19Since 523 is not divisible by any of these numbers Hence, 523 is a prime number
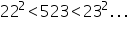 Prime numbers less than 23 are 2,3,5,7,11,13,17,19Since 523 is not divisible by any of these numbers Hence, 523 is a prime number
Prime numbers less than 23 are 2,3,5,7,11,13,17,19Since 523 is not divisible by any of these numbers Hence, 523 is a prime number
Q94. Prove that 263 is a prime number
Solution
256 < 263 < 289
162 < 263 < 172
Prime numbers that are less than 17 are 2,3,5,7,11,13
Since 263 is not divisible by any of these numbers, so 263 is a prime number.
Q95. Show that a number of the form n3 - n is always divisible by 6, where n is any positive integer.
Solution

Q96. If the polynomial f(x) = x4 - 6x3 + 16x2 - 26x + 10 is divided by another polynomial x2 - 2x + k, the remainder comes out to be x + a. Find k and a.
Solution
By the division algorithm,
Dividend = Divisor × Quotient + Remainder
Dividend - Remainder = Divisor × Quotient
Dividend - Remainder is always divisible by the divisor.
It is given that f(x) = x4 - 6x3 + 16x2 - 26x + 10 when divided by x2 - 2x + k leaves x + a as remainder. (1)
f(x) - (x + a) = x4 - 6x3 + 16x2 - 26x + 10 - a
is exactly divisible by x2 - 2x + k.
Let us now divide x4 - 6x3 + 16x2 - 26x + 10 - a by x2 - 2x + k (1)
Q97. Which of the following rational number has non-terminating and repeating decimal expansion?
Solution
Rational number 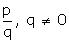 will be terminating decimal if the prime factorisation of q is of the form 2m
will be terminating decimal if the prime factorisation of q is of the form 2m 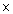 5n.
The denominator of the rational number
5n.
The denominator of the rational number 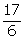 is not of the form 2m
is not of the form 2m 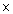 5n. Hence, it has non-terminating and repeating decimal expansion.
5n. Hence, it has non-terminating and repeating decimal expansion.
Q98. 
Solution

Q99. Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution
Let P(x, y) be equidistant from the points A(7, 1) and B(3, 5).
According to the question,
AP = BP
AP2 = BP2
(x - 7)2 + (y - 1)2 = (x - 3)2 + (y - 5)2 (1)
x2 - 14x + 49 + y2 - 2y + 1 = x2 - 6x + 9 + y2 - 10y + 25
−14x + 6x - 2y + 10y + 50 - 34 = 0
−8x + 8y + 16 = 0 (1)
−8x + 8y = −16
x - y = 2 which is the required relation. (1)
Q100. Find the greatest number of four digits which is divisible by 5,12 and 36.
Solution
The greatest number of four digits is 9999.
Any number which is divisible by all of 5, 12 and 36 has to be a least common multiple of 5, 12 and 36....
So, L.C.M. (5, 12, 36) =2 x 2 x 3 x 3 x 5=180...Now, 9999 is not divisible by 180 So the required number has to be less than 9999.On dividing 9999 by 180 we get Quotient=55 and Remainder=99.So the required number is 9999-99=9900.
So the greatest number of four digits which is divisible by 5,12, 36 is 9900
Q101. If sec θ + tan θ = x, show that sin θ = 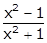 OR
If sec x = 5/4, evaluate
OR
If sec x = 5/4, evaluate 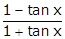
Solution
sec θ + tan θ = x
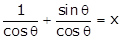
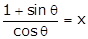 (1)
(1)
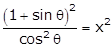
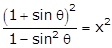 (1)
(1)
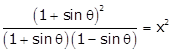
 (1)
By componendo-dividendo,
(1)
By componendo-dividendo,

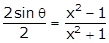
 (1)
OR
sec x =
(1)
OR
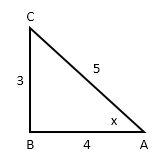
sec x = 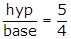 Consider triangle ABC, right angled at B.
Hypotenuse = AC = 5 units, Base = AB = 4 units and ∠BAC = x (1)
Consider triangle ABC, right angled at B.
Hypotenuse = AC = 5 units, Base = AB = 4 units and ∠BAC = x (1)
 (1)
AC2 = AB2 + BC2
52 = 42 + BC2
BC2 = 25 - 16 = 9
BC = 3
tan x = BC/AB = ¾ (1)
(1)
AC2 = AB2 + BC2
52 = 42 + BC2
BC2 = 25 - 16 = 9
BC = 3
tan x = BC/AB = ¾ (1)
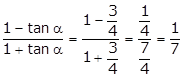 (1)
(1)
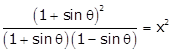
 (1)
AC2 = AB2 + BC2
52 = 42 + BC2
BC2 = 25 - 16 = 9
BC = 3
tan x = BC/AB = ¾ (1)
(1)
AC2 = AB2 + BC2
52 = 42 + BC2
BC2 = 25 - 16 = 9
BC = 3
tan x = BC/AB = ¾ (1)
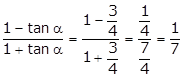 (1)
(1)
Q102. 
Solution

Q103. A rectangular lawn, 75 m by 60 m, has two roads, each 4 m wide, running through the middle of the lawn, one parallel to the length and the other parallel to the breadth, as shown in the figure. Find the cost of gravelling the roads at Rs. 4.50 per m2.
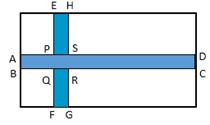

Solution
Area of the road ABCD = 75 × 4 = 300 m2
Area of the road EFGH = 60 × 4 = 240 m2 (1)
Area PQRS is common to both roads.
Area PQRS = 4 × 4 = 16 m2 (1)
Area of the roads to be gravelled = 300 + 240 - 16 = 524 m2 (1)
Q104. In a morning walk three persons steps off together. Their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that they can cover the distance in complete steps?
Solution
Required distance will be the L.C.M of 80cm, 85cm and 90cm.
Prime factorisation of 80, 85 and 90 are given by
80 = 2 × 2 × 2 × 2 × 5 = 24 × 5
85 = 5 × 17
90 = 2 × 3 × 3 × 5 = 2 × 32 × 5
LCM(80, 85, 90) = 24 × 32 × 5 × 17 = 12240 cm
Therefore the minimum distance thet should walk to cover the distance is 122m and 40cm.
Q105. Two persons jog together from the same point and in the same direction. One takes 12 minutes to jog one round while the other takes 18 minutes. After how many minutes will they meet first together at the starting point?
Solution
The two persons will be first together at the starting point after an interval of time which is the LCM of the times in which each of them make one complete round.
So, the required time will be the LCM of 12 and 18 minutes.
Prime factorisation of 12 and 18 are:
12 = 2  2
2  3
18 = 2
3
18 = 2 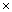 3
3 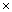 3
LCM (12, 18) = 2
3
LCM (12, 18) = 2 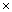 2
2 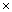 3
3 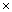 3 = 36
Thus, the two persons will together meet for the first time after 36 minutes.
3 = 36
Thus, the two persons will together meet for the first time after 36 minutes.
Q106. Without performing the long division whether the following rational numbers will have a terminating or a non-terminating repeating decimal expansion:
(i)  (ii)
(ii)  (iii)
(iii)  (iv)
(iv)  (v)
(v)  (vi)
(vi)  (vii)
(vii) 
Solution
(i) Non terminating repeating
(ii) Terminating
(iii) Non terminating repeating
(iv) Non terminating repeating
(v) Non terminating repeating
(vi) Non terminating repeating
(vii) Terminating
Q107. Prove that 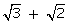 is irrational.
is irrational.
Solution
Suppose 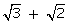 is rational.
is rational.
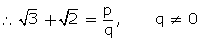 Squaring both sides, we get,
Squaring both sides, we get,
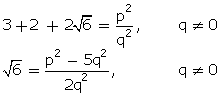
 is irrational while
is irrational while  is rational and an irrational number can never be equal to a rational number.
Thus our assumption is wrong.
Hence,
is rational and an irrational number can never be equal to a rational number.
Thus our assumption is wrong.
Hence,  is irrational.
is irrational.
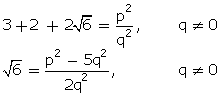
 is rational and an irrational number can never be equal to a rational number.
Thus our assumption is wrong.
Hence,
is rational and an irrational number can never be equal to a rational number.
Thus our assumption is wrong.
Hence,
Q108. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution
Let x be the maximum number of columns in which the two groups can march.
x is HCF of 616 and 32.
By Euclid's division algorithm,
616 = 32  19 + 8
32 = 8
19 + 8
32 = 8 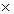 4 + 0
HCF (616, 32) = 8
Hence, the required maximum number of columns in which they can march is 8.
4 + 0
HCF (616, 32) = 8
Hence, the required maximum number of columns in which they can march is 8.
Q109. A solid sphere 6 cm in diameter is formed into a tube 10 cm in external diameter and 4 cm in length. Find the thickness of the tube.
Solution
Diameter of the sphere = 6 cm
Radius of the sphere = 3 cm
Volume =  (1)
As the external diameter of the tube is 10 cm,
External radius = 5 cm
Internal radius = 5 - x, where x cm = thickness the tube
And the length of the tube = 4 cm (1)
Volume of the material of the tube = External volume - Internal volume
= π × 52 × 4 - π(5 - x)2 × 4
= 4π [52 - (5 - x)2]
= 4π(10 - x)x cc (1)
According to the question,
36π = 4π(10 - x)x
10x - x2 = 9
x2 - 10x + 9 = 0
(x - 1)(x - 9) = 0
x = 1 or x = 9 which is neglected as the thickness of the tube cannot be more than its external radius.
Thickness of the tube = 1 cm (1)
(1)
As the external diameter of the tube is 10 cm,
External radius = 5 cm
Internal radius = 5 - x, where x cm = thickness the tube
And the length of the tube = 4 cm (1)
Volume of the material of the tube = External volume - Internal volume
= π × 52 × 4 - π(5 - x)2 × 4
= 4π [52 - (5 - x)2]
= 4π(10 - x)x cc (1)
According to the question,
36π = 4π(10 - x)x
10x - x2 = 9
x2 - 10x + 9 = 0
(x - 1)(x - 9) = 0
x = 1 or x = 9 which is neglected as the thickness of the tube cannot be more than its external radius.
Thickness of the tube = 1 cm (1)
Q110. If two triangles are equiangular, prove that the ratio of the corresponding sides is same as the ratio of the corresponding altitudes.
Solution
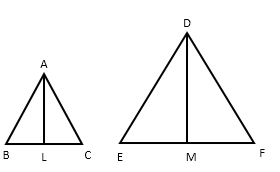 Given: Two triangles ABC and DEF in which ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and AL perpendicular to BC and DM perpendicular to EFb To prove:
Given: Two triangles ABC and DEF in which ∠A = ∠D, ∠B = ∠E, ∠C = ∠F and AL perpendicular to BC and DM perpendicular to EFb To prove:
Q111. A bag contains 5 red balls, 8 white balls, 4 green balls and 7 black balls. If one ball is drawn at random, find the probability that it is
Black
Red
Not green
OR
A jar contains 54 marbles each of which is blue, green or white. The probability of selecting a blue marble at random from the jar is 1/3, and the probability of selecting a green marble at random is 4/9. How many white marbles does the jar contain?
Solution
Total number of balls in the bag = 5 + 8 + 4 + 7 = 24
Total number of elementary events = 24
There are 7 black balls in the bag Favourable number of elementary events = 7 P(getting a black ball) = 7/24 (1)
There are 5 red balls in the bag Favourable number of elementary events = 5 P(getting a red ball) = 5/24 (1)
There are 5 + 8 + 7 = 20 balls which are not green. Favourable number of elementary events = 20 P(not getting a green ball) = 20/24 = 5/6 (1)
OR
Let there be b blue, g green and w white marbles in the jar. Then
b + g + w = 54 … (i)
P(selecting a blue marble) = b/54
The probability of getting a blue marble is 1/3.
1/3 = b/54
b = 18 (1)
P(selecting a green marble) = 4/9
g/54 = 4/9
g = 24 (1)
Put b = 18 and g = 24 in (i)
18 + 24 + w = 54
w = 12
Hence, the jar contains 12 white marbles. (1)
Q112. Why  is a non terminating rational number?
is a non terminating rational number?
Solution
120 = 23x 3 x 5
Because the prime factorization of denominator contains a prime factor 3 other 2 and 5. so  is a non- terminating rational number
is a non- terminating rational number
Q113. Use Euclid's algorithm to find H. C. F of 135 and 225.
Solution
Q114. Given that the sum and the difference of the H.C.F and L.C.M are 96 and 48 respectively. Find the product of the numbers.
Solution
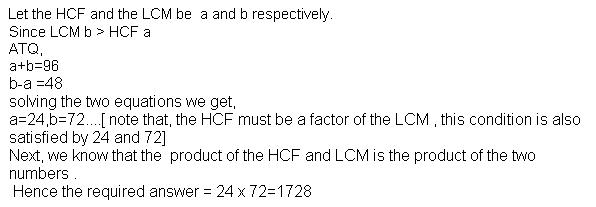
Q115. If the mean of the following frequency distribution is 54, then what is the value of p?
Class
0-20
20-40
40-60
60-80
80-100
Frequency
7
p
10
9
13
OR
Find the median daily wages from the following frequency distribution:
Daily wages in Rs.
100-150
150-200
200-250
250-300
300-350
Number of labourers
6
3
5
20
10
Solution
(1)
Class interval
Frequency
Mid-value xi
fi xi
0−20
7
10
70
20−40
p
30
30p
40−60
10
50
500
60−80
9
70
630
80−100
13
90
1170
∑fi = 39 + p
∑fixi = 2370 + 30p
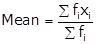
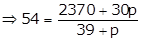 (1)
(1)
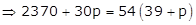
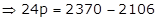
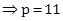 (1)
OR
(1)
Class
Frequency fi
Cumulative frequency
100−150
6
6
150−200
3
9
200−250
5
14
250−300
20
34
300−350
10
44
N = ∑fi = 44
N = 44
N/2 = 22
The cumulative frequency just greater than 22 is 34, and the corresponding class is 250−300.
Median class is 250−300.
l = 250, h = 30, f = 20, c = 14, N/2 = 22 (1)
Median = l +
(1)
OR
(1)
Class
Frequency fi
Cumulative frequency
100−150
6
6
150−200
3
9
200−250
5
14
250−300
20
34
300−350
10
44
N = ∑fi = 44
N = 44
N/2 = 22
The cumulative frequency just greater than 22 is 34, and the corresponding class is 250−300.
Median class is 250−300.
l = 250, h = 30, f = 20, c = 14, N/2 = 22 (1)
Median = l + 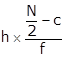 = 250 +
= 250 + 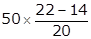 = 270
Hence, the median wages are Rs. 270. (1)
= 270
Hence, the median wages are Rs. 270. (1)
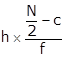 = 250 +
= 250 +
Q116. Find the H.C.F. between 24 and 404 and express it as a linear combination of the two numbers.
Solution
Since 404 > 24
By using Euclid's division lemma, we get
404 = 24 × 16 + 20
24 = 20 × 1 + 4
20 = 4 × 5 + 0
The remainder at this stage is zero.
So the divisor in the last step i.e 4 is the HCF.
Therefore HCF(24,404) = 4
Now working steps backward, we get
4 = 24 - (20 × 1)
= 24 - {[404 - (24 × 16)]}
= (24 × 17) - (404 × 1)
Hence, 4 = (24 × 17) - (404 × 1) is a linear combination of 24 and 404.
Q117. Find the value of k for which the equation kx2 - 6x - 2 = 0 has real roots.
OR
Solve: 2x2 - x + 1/8 = 0
Solution
kx2 - 6x - 2 = 0
Comparing with ax2 + bx + c = 0
a = k, b = −6, c = −2 (½)
b2 - 4ac = (−6)2 - 4 × k × (−2)
= 36 + 8k (½)
The given equation has real roots if D ≥ 0 (½)
36 + 8k ≥ 0
k ≥ −36/8
k ≥ −9/2 (½)
OR
2x2 - x + 1/8 = 0
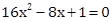
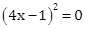 (1)
4x - 1 = 0
x = ¼ (½)
Hence, each of the two roots of the given equation is x = 1/4. (½)
(1)
4x - 1 = 0
x = ¼ (½)
Hence, each of the two roots of the given equation is x = 1/4. (½)
Q118. Solve the following system of equations for x and y.
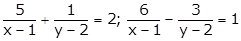
Solution
Q119. Show that one and only one out of n, n+3 n+6 or n+9 is divisible by 4.
Solution
Any positive integer is of the form 4q, 4q + 1, 4q + 2, 4q + 3 for some integer q.
Case (I):
When n = 4q, then n is divisible by 4
n + 3 = 4q + 3, leaves a remainder of 3 when divided by 4
n + 6 = 4q + 6, leaves a remainder of 2 when divided by 4
n + 9 = 4q + 9, leaves a remainder 1 when divided by 4
Case (II):
When n = 4q + 1, then it leaves a remainder 1 when divided by 4
n + 3 = 4q + 4 is divisible by 4.
n + 6 = 4q + 7, leaves a remainder 3 when divided by 4
n + 9 = 4q + 10, leaves a remainder 2 when divided by 4
Case (III):
When n = 4q + 2, then n + 6 = 4q + 8 is divisible by 4
n + 3 = 4q + 5, leaves a remainder of 1 when divided by 4
n + 6 = 4q + 8 is divisible by 4,
n + 9 = 4q + 11, leaves a remainder 3 when divided by 4
Case (IV):
When n = 4q + 3, leaves a remainder of 3 when divided by 4
n + 3 = 4q + 6, leaves a remainder of 2 when divided by 4
n + 6 = 4q + 9, leaves a remainder 1 when divided by 4
n + 9 = 4q + 12 is divisible by 4.
Thus, we see that in each case only one of the number n, n + 3, n + 9 is divisible by 4.
Hence proved.
Q120. If α, β are the zeroes of the quadratic polynomial f(x) = x2 - px + q, then find the values of α2 + β2 and 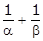 .
.
Solution
Since α and β are the zeroes of a polynomial f(x) = x2 - px + q,
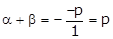 and
and 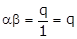 (1)
(1)
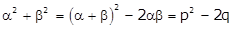 (1)
(1)
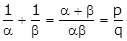 (1)
(1)
Q121. Show that the square of any positive odd integer is of the form 8m + 1, for some integer m.
Solution
Let a be any positive integer and b = 4.
Then, by Euclid's algorithm a = 4q + r for some integer q 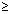 0 and 0
0 and 0  r < 4
Thus, r = 0, 1, 2, 3
Since, a is an odd integer, so a = 4q + 1 or 4q + 3
Case I: When a = 4q + 1
Squaring both sides, we have, a2 = (4q + 1)2
a2 = 16q2 + 1 + 8q
= 8(2q2 + q) + 1
= 8m + 1, where m = 2q2 + q
Case II: When a = 4q + 3
Squaring both sides, we have,
a2 = (4q +3)2
= 16q2 + 9 + 24q
= 16 q2 + 24q + 8 + 1
= 8(2q2 + 3q + 1) +1
= 8m +1 where m = 2q2 + 3q + 1
Hence, a is of the form 8m + 1 for some integer m.
r < 4
Thus, r = 0, 1, 2, 3
Since, a is an odd integer, so a = 4q + 1 or 4q + 3
Case I: When a = 4q + 1
Squaring both sides, we have, a2 = (4q + 1)2
a2 = 16q2 + 1 + 8q
= 8(2q2 + q) + 1
= 8m + 1, where m = 2q2 + q
Case II: When a = 4q + 3
Squaring both sides, we have,
a2 = (4q +3)2
= 16q2 + 9 + 24q
= 16 q2 + 24q + 8 + 1
= 8(2q2 + 3q + 1) +1
= 8m +1 where m = 2q2 + 3q + 1
Hence, a is of the form 8m + 1 for some integer m.
Q122. Prove that  is an irrational.
OR
Prove that
is an irrational.
OR
Prove that 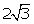 - 7 is an irrational.
- 7 is an irrational.
Solution
Let  be a rational number
be a rational number
 Let
Let  =
= 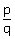 where p and q are co-prime.
So,
where p and q are co-prime.
So, 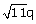 = p
11q2 = p2
Thus, 11 divides p2.
Hence 11 divides p.… (1)
Let p = 11c
11q2 = 121 c2
Or q2 = 11c2
This implies that 11 divides q2.
Hence 11 divides q.… (2)
From (1) and (2), we can say that:
p and q have a common factor 11 which contradicts our assumption.
Hence,
= p
11q2 = p2
Thus, 11 divides p2.
Hence 11 divides p.… (1)
Let p = 11c
11q2 = 121 c2
Or q2 = 11c2
This implies that 11 divides q2.
Hence 11 divides q.… (2)
From (1) and (2), we can say that:
p and q have a common factor 11 which contradicts our assumption.
Hence,  is irrational.
OR
Let
is irrational.
OR
Let 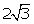 - 7 be rational.
- 7 be rational.

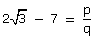 where p and q are co-prime
where p and q are co-prime
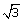 =
=  Since p and q are integers,
Since p and q are integers,  is rational.
is rational.

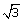 is rational
But we know that
is rational
But we know that 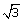 is irrational
is irrational
 Our assumption is wrong.
Hence 2
Our assumption is wrong.
Hence 2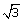 - 7 is irrational.
- 7 is irrational.
Q123. A kite is
flying at a height of 75 m from the level ground, attached to a string
inclined at 60° to the horizontal. Find the
length of the string, assuming that there is no slack in it.
Solution
Let the length of the string be l
m.
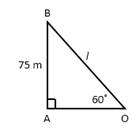
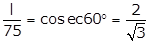 (½)
(½)
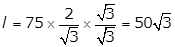 (½)
(½)

Q124. Show by an example that the sum and product of two irrational numbers is not always an irrational number.
Solution
Consider two numbers A=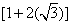 and B=
and B=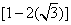 We see that A*B=
We see that A*B= = -11, which is a rational number.
A+B=
= -11, which is a rational number.
A+B=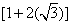 +
+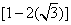 =2, which also is a rational number.
So we see that , the sum and product of two irrational numbers is not always an irrational number.
=2, which also is a rational number.
So we see that , the sum and product of two irrational numbers is not always an irrational number.
Q125. Show that, any positive integer is of form 3q, 3q + 1 or 3q + 2, where q is some integer.
Solution
Euclid's Division Lemma : For any two positive integers a and b, there exists two unique integers q and r such that a = bq + r, 0 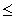 r < b.
If we take b = 3, the possible values of r will be 0, 1 and 2
Hence, either a = 3q or a = 3q + 1 or a = 3q + 2.
r < b.
If we take b = 3, the possible values of r will be 0, 1 and 2
Hence, either a = 3q or a = 3q + 1 or a = 3q + 2.
Q126. The marks obtained in a class test by 30 students of a class are as follows:
Marks obtained
Number of students
More than or equal to 5
30
More than or equal to 10
28
More than or equal to 15
16
More than or equal to 20
14
More than or equal to 25
10
More than or equal to 30
7
More than or equal to 35
3
Draw less than type and more than type ogive curves for the given data and hence find the median.
OR
The mode of the following frequency distribution is 55 and the modal class is 45-60. Find the value of p and q.
Class Interval
0-15
15-30
30-45
45-60
60-75
75-90
Total
Frequency
6
7
p
15
10
q
51
Solution
More than method:
Marks obtained
Number of students
More than or equal to 5
30
More than or equal to 10
28
More than or equal to 15
16
More than or equal to 20
14
More than or equal to 25
10
More than or equal to 30
7
More than or equal to 35
3
(1)
Thus, we plot the points (5, 30), (10, 28), (15, 16), (20, 14), (25, 10), (30, 7), (35, 3).
Less than method:
Marks obtained
No. of students
(Frequency)
Marks less than
Cumulative frequency
5-10
30 - 28 = 2
10
2
10-15
28 - 16 = 12
15
14
15-20
16 - 14 = 2
20
16
20-25
14 - 10 = 4
25
20
25-30
10 - 7 = 3
30
23
30-35
7 - 3 = 4
35
27
35-40
3 - 0 = 3
40
30
(1)
We plot points (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27) and (40, 30) to get the ‘less than’ curve.
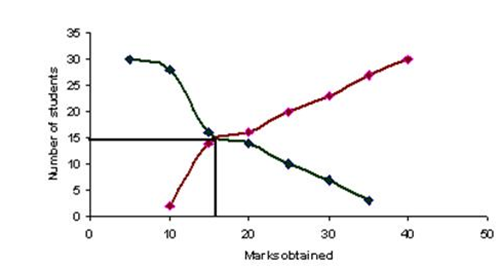 Median = 17. 5 (x-coordinate of intersection of both curves) (2)
OR
We have 38 + p + q = 51
p + q = 51 − 38
p + q = 13 … (1)
Mode = 55 (Given)
∴ Modal class is 45 − 60
Median = 17. 5 (x-coordinate of intersection of both curves) (2)
OR
We have 38 + p + q = 51
p + q = 51 − 38
p + q = 13 … (1)
Mode = 55 (Given)
∴ Modal class is 45 − 60
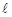 = 45, f0 = p, f1 = 15, f2 = 10, h = 15 (1)
55 = 45 +
= 45, f0 = p, f1 = 15, f2 = 10, h = 15 (1)
55 = 45 + 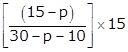 10 =
10 = 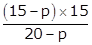 200 − 10p = 225 − 15p (1)
5p = 25
p = 5
From (1), we have
q = 13 − 5 = 8 (1)
200 − 10p = 225 − 15p (1)
5p = 25
p = 5
From (1), we have
q = 13 − 5 = 8 (1)
 Median = 17. 5 (x-coordinate of intersection of both curves) (2)
OR
We have 38 + p + q = 51
p + q = 51 − 38
p + q = 13 … (1)
Mode = 55 (Given)
∴ Modal class is 45 − 60
Median = 17. 5 (x-coordinate of intersection of both curves) (2)
OR
We have 38 + p + q = 51
p + q = 51 − 38
p + q = 13 … (1)
Mode = 55 (Given)
∴ Modal class is 45 − 60
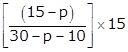 10 =
10 =
Q127. Show that 8n cannot end with the digit zero for any natural number n.
Solution
We know 8n = (23)n = 23n
If 8n end with zero then 10 is factor of 8n.
 8n = 23n =
8n = 23n = 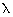 (5)(2)
(5)(2)
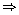 5 is factor of 2, which is a contradiction
So, our assumption is wrong. Hence 8n cannot end with zero.
5 is factor of 2, which is a contradiction
So, our assumption is wrong. Hence 8n cannot end with zero.
Q128. Show that any positive odd integer is of the form 4q + 1 or 4q + 3 where q is a positive.
Solution
Let 'a' any odd positive integer and b = 4
Using Euclid Division Lemma,
a = 4q + r, where 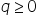 and 0
and 0  r < 4
r < 4
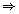 a = 4q or 4q + 1 or 4q + 2 or 4q + 3
a = 4q or 4q + 1 or 4q + 2 or 4q + 3 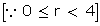
 a = 4q + 1 or 4q + 3
a = 4q + 1 or 4q + 3 
 Any odd integer is of the form 4q + 1 or 4q + 3
Any odd integer is of the form 4q + 1 or 4q + 3
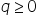 and 0
and 0
Q129. Without actually performing the long division, state whether the following number will have a terminating decimal or a non-terminating repeating decimal expansion.
(i)  (ii)
(ii)  (iii)
(iii) 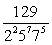
Solution
(i) 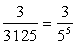 Here, the prime factorisation of denominator is of the form
Here, the prime factorisation of denominator is of the form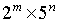 .
Hence, the decimal expansion of the given rational number is terminating.
(ii)
.
Hence, the decimal expansion of the given rational number is terminating.
(ii) 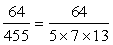 Here, the prime factorisation of denominator is not of the form
Here, the prime factorisation of denominator is not of the form 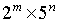 .
So, the decimal expansion of the given rational number is non - terminating repeating.
(iii)
.
So, the decimal expansion of the given rational number is non - terminating repeating.
(iii) 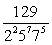 Here, the denominator is not of the form
Here, the denominator is not of the form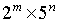 .
Hence, the decimal expansion of the given rational number is non - terminating repeating.
.
Hence, the decimal expansion of the given rational number is non - terminating repeating.
Q130. Find the LCM of 72, 80 and 120 using the fundamental theorem of arithmetic.
Solution
72 = 23  32, 80 = 24
32, 80 = 24  5, 120 = 23
5, 120 = 23  3
3  5
5
 LCM (72, 80, 120) = 24
LCM (72, 80, 120) = 24  32
32  5 = 720
5 = 720
Q131. Show that the square of any positive integer is of the form 4q or 4q + 1 for some integer q.
Solution
Applying Euclid's division algorithm with a and b = 4.
a = 4Q + r, 0 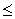 r < 4
When r = 0, a = 4Q
r < 4
When r = 0, a = 4Q  a2 = 16Q2 = 4(4Q2) = 4q, where q = 4Q2
When r = 1, a = 4Q + 1
a2 = 16Q2 = 4(4Q2) = 4q, where q = 4Q2
When r = 1, a = 4Q + 1
 a2 = (4Q + 1)2 = 16Q2 + 1 + 8Q = 4Q(4Q + 2) + 1 = 4q + 1, where q = Q(4Q + 2)
When r = 2, a = 4Q + 2
a2 = (4Q + 1)2 = 16Q2 + 1 + 8Q = 4Q(4Q + 2) + 1 = 4q + 1, where q = Q(4Q + 2)
When r = 2, a = 4Q + 2
 a2 = (4Q + 2)2 = 16Q2 + 4 + 16Q = 4(4Q2 + 4Q + 1) = 4q, where q = 4Q2 + 4Q + 1
When r = 3, a = 4Q + 3
a2 = (4Q + 2)2 = 16Q2 + 4 + 16Q = 4(4Q2 + 4Q + 1) = 4q, where q = 4Q2 + 4Q + 1
When r = 3, a = 4Q + 3
 a2 = (4Q + 3)2 = 16Q2 + 9 + 24Q = 4(4Q2 + 6Q + 2) + 1 = 4q + 1, where q = 4Q2 + 6Q + 2
Hence, the square of any positive integer is of the form 4q or 4q + 1 for some integer q.
a2 = (4Q + 3)2 = 16Q2 + 9 + 24Q = 4(4Q2 + 6Q + 2) + 1 = 4q + 1, where q = 4Q2 + 6Q + 2
Hence, the square of any positive integer is of the form 4q or 4q + 1 for some integer q.
Q132. A die is
thrown at once. What is the probability of getting a number other than 4?
OR
One card is drawn at random from a
well-shuffled deck of 52 cards. What is the probability that the card drawn
is a face card?
Solution
In a single throw of a
die, all possible outcomes are 1, 2, 3, 4, 5, 6.
Total number of possible outcomes = 6
Let E be the event of getting a number
other than 4.
Then, the favourable outcomes are 1, 2, 3,
5, 6.
Number of favourable outcomes = 5 (½)
P(getting a number other than 4) = P(E) = 5/6 (½)
OR
Total number of possible outcomes = 52
We know that kings, queens and jacks are
face cards.
Number of face cards = 12
Let E be the
event of getting a face card.
The
number of favourable outcomes = 12 (½)
P(getting a face card) = 12/52 =
3/13 (½)
Q133. Find without
actual division whether the 66/180 rational number is a terminating or
non-terminating repeating decimal.
OR
Show that any number of
the form 6n, n ∊ N can never end with digit 0.
Solution
Q134. Find LCM and HCF of 120 and 144 by fundamental theorem of Arithmetic.
Solution
120 = 23 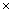 3
3 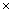 5
144 = 24
5
144 = 24 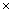 32
LCM = 24
32
LCM = 24 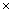 32
32 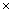 5 = 720
HCF = 23
5 = 720
HCF = 23 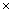 3 = 24
3 = 24
Q135. Find the HCF and LCM of 42, 72, and 120 using prime factorization
Solution
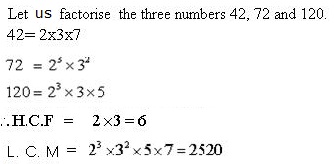
Q136. The measure of the angle of depression of the bottom of a building on a level ground from the top of a tower 50 m high is 60˚. How far is the building from the tower?
Solution
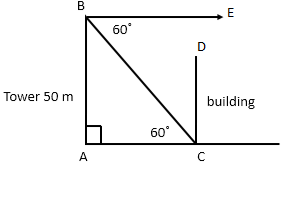 (1)
Let AB be the tower and CD be the building.
AB = 50 m
Angle of depression ∠CBE = 60°
∠BCA = 60°
In right-angled triangle CAB,
tan 60° = AB/AC
(1)
Let AB be the tower and CD be the building.
AB = 50 m
Angle of depression ∠CBE = 60°
∠BCA = 60°
In right-angled triangle CAB,
tan 60° = AB/AC
Comments
Post a Comment